Content

• Steps
• Part 1 of 2: Angles in radians
• Part 2 of 2: x-y coordinates (cosine, sine)
• Tips

The unit circle is used not only in trigonometry and geometry, but also in other branches of mathematics. At first glance, remembering all the singular points on it is rather difficult, but if you understand the basic principle, you can easily use the unit circle.

Steps

Part 1 of 2: Angles in radians

1. 1 Draw two perpendicular lines. Take a large piece of paper and a ruler and draw vertical and horizontal lines. The intersection point of these lines should lie approximately in the center of the sheet. These will be the axes x and y.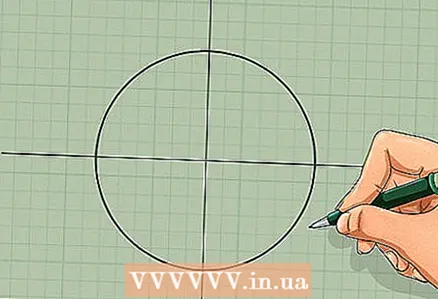
2. 2 Draw a circle. Take a compass, put its needle at the intersection of the lines and draw a large circle.
3. 3 Become familiar with the concept of a radian. Radian is the unit of measure for angles. By definition, an angle of one radian cuts off at the circumference of the unit radius an arc of unit length. In this section, points will be denoted by their corresponding values ​​in radians. If you remember the relationship between the circumference of a circle and its radius, you can easily determine these values ​​along the unit circle, even if you forgot them.
   • When measuring angles along the unit circle, the point with coordinates (0; 1) is always taken as the starting point. For clarity, you can imagine the unit circle in the form of a wind rose, then the reference point will correspond to the east direction.
4. 4 Remember that the total length of the unit circle is 2π. The circumference is 2πr, where r - its radius. Since the radius of the unit circle is 1, its length is 2π. From here, you can find the value in radians for each point of the circle: just take 2π and divide by the fraction of the circle that corresponds to this point. This is much easier than trying to learn the values ​​at each point on the unit circle.
5. 5 Mark four points on the axes x and y. These points will divide the circle into four quadrants (quarters):
   • "east" is the reference point, so it corresponds to 0 radians;
   • "north" = ¼ circle = /₄ = /₂ radians;
   • "west" = half circle = /₂ = π radians;
   • "south" = three quarters of a circle = 2π * ¾ = /₂ radians;
   • after traversing the whole circle, we return to the starting point, so along with 0 it can be assigned the value 2π.
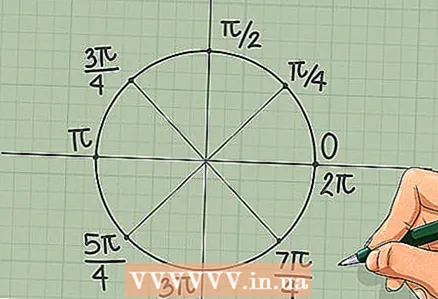6. 6 Divide the circle into eight parts. Draw straight lines down the middle of each quadrant so that they halve them. For the points of intersection of lines with a circle, we obtain the following values ​​in radians:
   • /₄;
   • /₄;
   • /₄;
   • /₄;
   • (points π / 2, π, 3π / 2 and 2π are already marked).
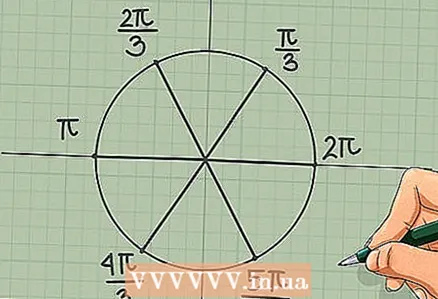7. 7 Divide the circle into six parts. Draw additional lines that divide the circle into six parts. You can use a protractor for this: start from the positive direction of the axis x and set aside 60 degree angles. Using the method described above, it is easy to determine that the sixth part of the circle is /₆ = /₃ radians. Now we can mark the intersection points of the new lines with the circle (one in each quadrant):
   • /₃;
   • /₃;
   • /₃;
   • /₃;
   • (the values ​​of π and 2π have already been noted).
8. 8 Draw lines that divide the circle into 12 parts. It remains to divide the unit circle into 12 equal parts. Of these points, only four were not previously noted:
   • /₆;
   • /₆;
   • /₆;
   • /₆.

Part 2 of 2: x-y coordinates (cosine, sine)

1. 1 Become familiar with the concepts of sine and cosine. The unit circle is great for working with right-angled triangles. Coordinates x points lying on the circle are equal to cos (θ), and the coordinates y correspond to sin (θ), where θ is the angle.
   • If you find it difficult to remember this rule, just remember that in the pair (cos; sin) "sine is in last place".
   • This rule can be deduced if we consider right-angled triangles and the definition of these trigonometric functions (the sine of the angle is equal to the ratio of the length of the opposite, and the cosine is the adjacent leg to the hypotenuse).
2. 2 Write down the coordinates of the four points on the circle. A "unit circle" is a circle whose radius is equal to one. Use this to determine coordinates x and y at four points of intersection of the coordinate axes with the circle. Above, we have designated these points for clarity as "east", "north", "west" and "south", although they do not have an established name.
   • "East" corresponds to a point with coordinates (1; 0).
   • "North" corresponds to a point with coordinates (0; 1).
   • "West" corresponds to a point with coordinates (-1; 0).
   • "South" corresponds to a point with coordinates (0; -1).
   • This is the same as a normal graph, so there is no need to memorize these values, just remember the basic principle.
3. 3 Remember the coordinates of the points in the first quadrant. The first quadrant is located at the top right of the circle, where the coordinates are x and y take positive values. These are the only coordinates you need to remember:
   • dot /₆ has coordinates (${ displaystyle { frac { sqrt {3}} {2}}, { frac {1} {2}}}$);
   • dot /₄ has coordinates (${ displaystyle { frac { sqrt {2}} {2}}, { frac { sqrt {2}} {2}}}$);
   • dot /₃ has coordinates (${ displaystyle { frac {1} {2}}, { frac { sqrt {3}} {2}}}$);
   • note that the numerator only accepts three values. If you move in the positive direction (from left to right along the axis x and from bottom to top along the axis y), the numerator takes the values ​​1 → √2 → √3.
4. 4 Draw straight lines and determine the coordinates of the points of their intersection with the circle. If you draw straight horizontal and vertical lines from the points of one quadrant, the second points of intersection of these lines with the circle will have coordinates x and y with the same absolute values, but different signs. In other words, you can draw horizontal and vertical lines from the points of the first quadrant and sign the points of intersection with the circle with the same coordinates, but at the same time leave room for the correct sign ("+" or "-") on the left.
   • For example, you can draw a horizontal line between points /₃ and /₃... Since the first point has coordinates (${ displaystyle { frac {1} {2}}, { frac { sqrt {3}} {2}}}$), the coordinates of the second point will be (?${ displaystyle { frac {1} {2}},? { frac { sqrt {3}} {2}}}$), where a question mark is placed instead of the "+" or "-" sign.
   • Use the simplest method: note the denominators of the point coordinates in radians. All points with denominator 3 have the same absolute coordinate values. The same applies to points with denominators 4 and 6.
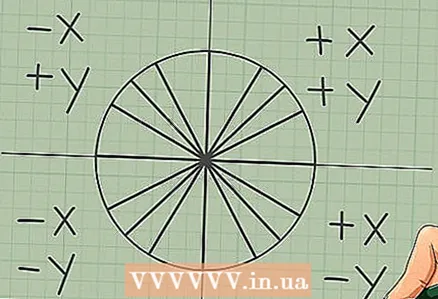5. 5 Use the symmetry rules to determine the sign of the coordinates. There are several ways to determine where to put the "-" sign:
   • remember the basic rules for regular charts. Axis x negative on the left and positive on the right. Axis y negative below and positive above;
   • start in the first quadrant and draw lines to other points. If the line crosses the axis y, coordinate x will change its sign. If the line crosses the axis x, the sign of the coordinate will change y;
   • remember that in the first quadrant all functions are positive, in the second quadrant only the sine is positive, in the third quadrant only the tangent is positive, and in the fourth quadrant only the cosine is positive;
   • whichever method you use, the first quadrant should be (+, +), the second (-, +), the third (-, -), and the fourth (+, -).
6. 6 Check if you are wrong. Below is a complete list of coordinates of "special" points (except for four points on the coordinate axes), if you move along the unit circle counterclockwise. Remember that to determine all these values, it is enough to remember the coordinates of the points only in the first quadrant:
   • first quadrant: (${ displaystyle { frac { sqrt {3}} {2}}, { frac {1} {2}}}$); (${ displaystyle { frac { sqrt {2}} {2}}, { frac { sqrt {2}} {2}}}$); (${ displaystyle { frac {1} {2}}, { frac { sqrt {3}} {2}}}$);
   • second quadrant: (${ displaystyle - { frac {1} {2}}, { frac { sqrt {3}} {2}}}$); (${ displaystyle - { frac { sqrt {2}} {2}}, { frac { sqrt {2}} {2}}}$); (${ displaystyle - { frac { sqrt {3}} {2}}, { frac {1} {2}}}$);
   • third quadrant: (${ displaystyle - { frac { sqrt {3}} {2}}, - { frac {1} {2}}}$); (${ displaystyle - { frac { sqrt {2}} {2}}, - { frac { sqrt {2}} {2}}}$); (${ displaystyle - { frac {1} {2}}, - { frac { sqrt {3}} {2}}}$);
   • fourth quadrant: (${ displaystyle { frac {1} {2}}, - { frac { sqrt {3}} {2}}}$); (${ displaystyle { frac { sqrt {2}} {2}}, - { frac { sqrt {2}} {2}}}$); (${ displaystyle { frac { sqrt {3}} {2}}, - { frac {1} {2}}}$).

Tips

• If you need to use the unit circle for a test or exam, draw it on a draft.
• With some practice, you should be able to quickly draw a unit circle. Over time, you will only be able to draw axes x and y or even do without a diagram.