Content

• Steps
• Method 1 of 3: Determining the Area of ​​a Square or Rectangle
• Method 2 of 3: Calculating the Area of ​​Other Shapes
• Method 3 of 3: Converting area to square centimeters from other units

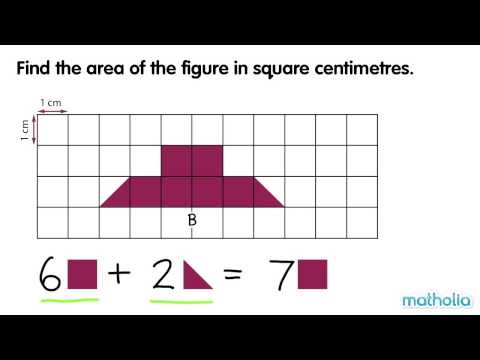
Determining the area of ​​flat figures in square centimeters (also referred to as cm) is quite simple. In the easiest case, when you need to calculate the area of ​​a square or rectangle, it is calculated by the product length and width... The area of ​​other shapes (circles, triangles, etc.) can be determined using a number of special mathematical formulas. Also, if required, you can easily convert the area to square centimeters from other units of measurement.

Steps

Method 1 of 3: Determining the Area of ​​a Square or Rectangle

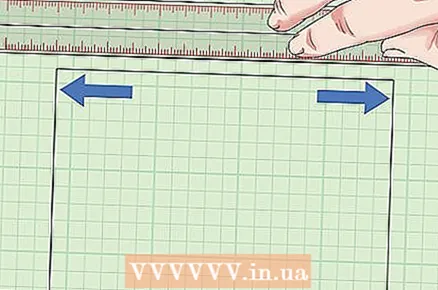1. 1 Define the length measured area. Squares and rectangles have four sides at right angles to each other. In the case of rectangles, their opposite sides are equal to each other, while all sides of squares are equal. Measure one side of the square or the larger side of the rectangle to determine its length in centimeters.
2. 2 Define width measured area. Next, measure in centimeters either side adjacent to the one you measured in the first place. This side will be at a 90 degree angle to the first. The second dimension will be the width of the square or rectangle.
   • Since all sides of a square are the same, its length will be equal to its width. Therefore, a square can initially only measure one side.
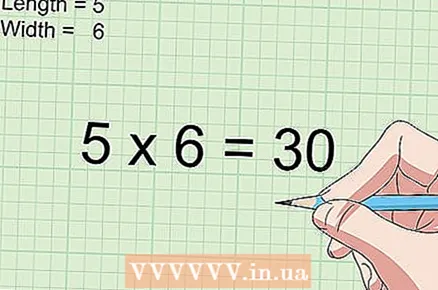3. 3 Multiply the length by the width. Simply multiply the length and width of the shape to find the area of ​​a square or rectangle in square centimeters.
   • For example, let's say the rectangle is 4 cm long and 3 cm wide.In this case, the area of ​​the figure is calculated as follows: 4 × 3 = 12 square centimeters.
   • In the case of a square (due to equal sides), you can simply multiply the length of one of its sides by itself (in other words, square it or to the second power) to determine the area of ​​the figure in square centimeters.

Method 2 of 3: Calculating the Area of ​​Other Shapes

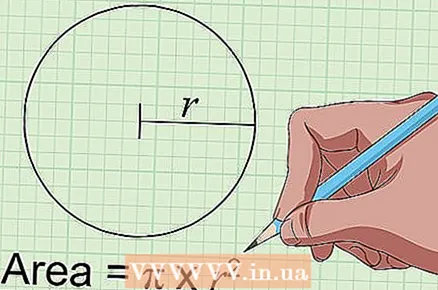1. 1 Find the area of ​​a circle using the formula: S = π × r. To find the area of ​​a circle in square centimeters, you need to know the distance in centimeters from the center of the circle to the line of its circumference. This distance is called radius circles. Once the radius is known, designate it with the letter r from the above formula. Multiply the radius value by itself and by a number π (3.1415926 ...) to find the area of ​​a circle in square centimeters.
   • For example, the area of ​​a circle with a radius of 4 cm is 50.27 square centimeters as a result of multiplying 3.14 and 16.
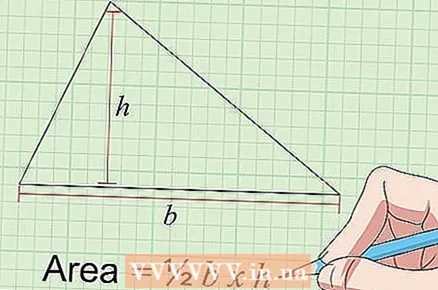2. 2 Calculate the area of ​​a triangle using the formula: S = 1/2 b × h. The area of ​​a triangle in square centimeters is calculated by multiplying half the length of its base b (in centimeters) to its height h (in centimeters). One of its sides is chosen as the base of the triangle, while the height of the triangle is the perpendicular, lowered to the base of the triangle from the vertex opposite to it. The area of ​​a triangle can be calculated through the length of the base and the height along either side of the triangle and the vertex opposite to it.
   • For example, if the base of the triangle is 4 cm long and the height drawn to the base is 3 cm, the area will be: 2 x 3 = 6 square centimeters.
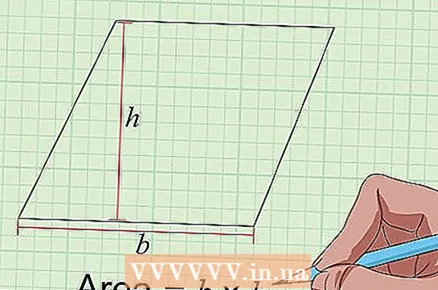3. 3 Find the area of ​​the parallelogram using the formula: S = b × h. Parallelograms are similar to rectangles with one exception - their angles are not necessarily 90 degrees. Accordingly, the calculation of the parallelogram area is performed in the same way for a rectangle: the length of the side of the base in centimeters is multiplied by the height of the parallelogram in centimeters. Any side is taken for the base, and the height is determined by the length of the perpendicular to it from the opposite obtuse corner of the figure.
   • For example, if the length of the base of a parallelogram is 5 cm and its height is 4 cm, its area will be: 5 x 4 = 20 square centimeters.
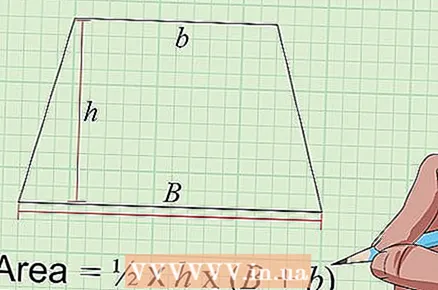4. 4 Calculate the area of ​​a trapezoid using the formula: S = 1/2 × h × (B + b). A trapezoid is a quadrangle whose two sides are parallel to each other, and the other two are not. To determine the area of ​​a trapezoid in square centimeters, you need to know three measures (in centimeters): the length of the longer parallel side B, the length of the shorter parallel side b and the height of the trapezoid h (defined as the shortest distance between its parallel sides along a segment perpendicular to them). Add the lengths of the two parallel sides together, halve the sum, and multiply by the height to get the area of ​​the trapezoid in square centimeters.
   • For example, if the longer of the parallel sides of the trapezoid is 6 cm, the shorter is 4 cm, and the height is 5 cm, the area of ​​the figure will be: ½ x (6 + 4) x 5 = 25 square centimeters.
5. 5 Find the area of ​​a regular hexagon: S = ½ × P × a. The above formula is only true for a regular hexagon with six equal sides and six equal angles. By letter P the perimeter of the figure is indicated (or the product of the length of one side by six, which is true for a regular hexagon). By letter a the length of the apothem is indicated - the distance from the center of the hexagon to the middle of one of its sides (a point located in the middle between two adjacent vertices of the figure). Multiply the perimeter and apothem in centimeters and divide the result by two to find the area of ​​a regular hexagon.
   • For example, if a regular hexagon has six equal sides of 4 cm each (that is, its perimeter is P = 6 x 4 = 24 cm), and the length of the apothem is 3.5 cm, then its area will be: ½ x 24 x 3.5 = 42 square centimeters.
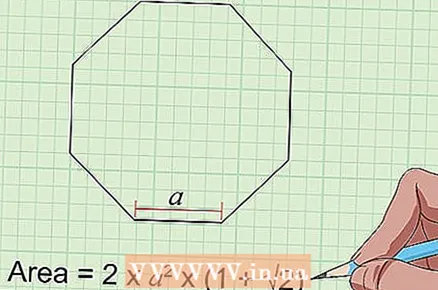6. 6 Calculate the area of ​​a regular octagon using the formula: S = 2a² × (1 + √2). To calculate the area of ​​a regular octagon (with eight equal sides and eight equal corners), you only need to know the length of one of the sides of the figure in centimeters (denoted by the letter “a” in the formula). Plug in the appropriate value into the formula and calculate the result.
   • For example, if the side length of a regular octagon is 4 cm, then the area of ​​this figure is: 2 x 16 x (1 + 1.4) = 32 x 2.4 = 76.8 square centimeters.

Method 3 of 3: Converting area to square centimeters from other units

1. 1 Convert all measurements to centimeters before calculating the area. In order to immediately calculate the area in square centimeters, it is necessary to substitute all the parameters in the formula for calculating the area also in centimeters (this applies to length, height, apothem, and so on). Therefore, if your original data is expressed in other units of measurement (for example, in meters), they should first be converted to centimeters. Below are the ratios of the most popular units of measurement.
   • 1 meter = 100 centimeters
   • 1 centimeter = 10 millimeters
   • 1 inch = 2.54 centimeters
   • 1 foot = 30.48 centimeters
   • 1 centimeter = 0.3937 inches
2. 2 To convert the area from square meters to square centimeters, it must be multiplied by 10,000 (that is, the area of ​​one square meter in centimeters), or by the product of 100 cm by 100 cm. If you know the area of ​​a figure in square meters, it can be converted to square centimeters by multiplying by 10,000.
   • For example, 0.5 square meter = 0.5 x 10000 = 5000 square centimeters.
3. 3 To convert square inches to square centimeters, multiply by 6.4516. As mentioned, 1 inch is equal to 2.54 centimeters, while a square inch is 6.4516 square centimeters (or 2.54 x 2.54). So, if you need to convert an area of ​​10 square inches to square centimeters, multiply 10 by 6.4516 to get 64.5 square centimeters.
   • It should also be mentioned that one hectare contains 10,000 square meters, while each square meter is equal to 10,000 square centimeters. Therefore, to express one hectare in centimeters, you must multiply 10,000 by 10,000 to get 100 million square centimeters.