Content

• Steps

An irrational equation is an equation in which the variable is under the root sign. To solve such an equation, it is necessary to get rid of the root. However, this can lead to the appearance of extraneous roots that are not solutions to the original equation. To identify such roots, it is necessary to substitute all found roots in the original equation and check whether the equality is true.

Steps

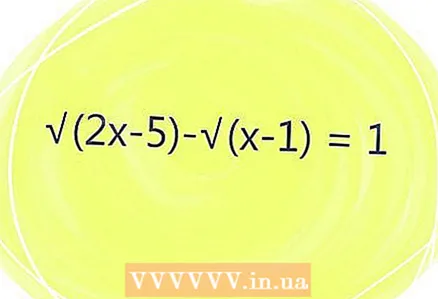1. 1 Write down the equation.
   • It is recommended to use a pencil to be able to correct mistakes.
   • Consider an example: √ (2x-5) - √ (x-1) = 1.
   • Here √ is the square root.
2. 2 Isolate one of the roots on one side of the equation.
   • In our example: √ (2x-5) = 1 + √ (x-1)
3. 3 Square both sides of the equation to get rid of one root.
4. 4 Simplify the equation by adding / subtracting similar terms.
5. 5 Repeat the above process to get rid of the second root.
   • To do this, isolate the remaining root on one side of the equation.
   • Square both sides of the equation to get rid of the remaining root.
6. 6 Simplify the equation by adding / subtracting similar terms.
   • 
   • Add / subtract similar terms, and then move all terms of the equation to the left and make them equal to zero. You will get a quadratic equation.
7. 7 Solve the quadratic equation using the quadratic formula.
   • The solution to a quadratic equation is shown in the following figure:
   • You get: (x - 2.53) (x - 11.47) = 0.
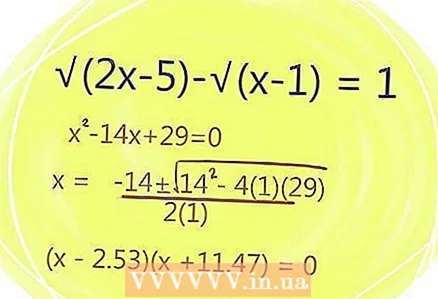
   • Thus, x1 = 2.53 and x2 = 11.47.
8. 8 Plug the found roots into the original equation and discard the extraneous roots.
   • Plug in x = 2.53.
   • - 1 = 1, that is, equality is not observed and x1 = 2.53 is an extraneous root.
   • Plug in x2 = 11.47.
   • Equality is met and x2 = 11.47 is the solution to the equation.
   • Thus, discard the extraneous root x1 = 2.53 and write down the answer: x2 = 11.47.