Content

• Steps
• Method 1 of 3: Part 1: Determining the Inflection Point
• Method 2 of 3: Calculating the Derivatives of a Function
• Method 3 of 3: Part 3: Find the Inflection Point
• Tips

In differential calculus, an inflection point is a point on a curve at which its curvature changes sign (from plus to minus or from minus to plus). This concept is used in mechanical engineering, economics and statistics to identify significant changes in data.

Steps

Method 1 of 3: Part 1: Determining the Inflection Point

1. 1 Definition of a concave function. The middle of any chord (a segment connecting two points) of the graph of a concave function lies either under the graph or on it.
2. 2 Definition of a convex function. The middle of any chord (a segment connecting two points) of the graph of a convex function lies either above the graph or on it.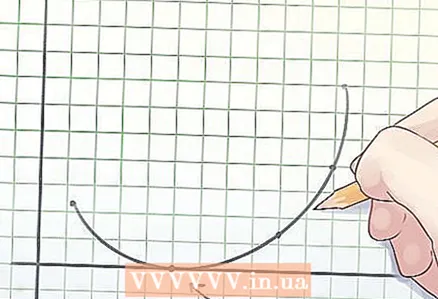
3. 3 Determination of the roots of the function. The root of a function is the value of the variable "x" at which y = 0.
   • When plotting a function, the roots are the points at which the graph crosses the x-axis.

Method 2 of 3: Calculating the Derivatives of a Function

1. 1 Find the first derivative of the function. Look at the rules of differentiation in the textbook; you have to learn to take the first derivatives, and only then move on to more complex calculations. The first derivatives are designated f '(x). For expressions of the form ax ^ p + bx ^ (p − 1) + cx + d, the first derivative is: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • For example, find the inflection points of the function f (x) = x ^ 3 + 2x -1. The first derivative of this function is:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Find the second derivative of the function. The second derivative is the derivative of the first derivative of the original function. The second derivative is denoted as f ′ ′ (x).
   • In the above example, the second derivative is:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Set the second derivative to zero and solve the resulting equation. The result will be the expected inflection point.
   • In the above example, your calculation looks like this:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Find the third derivative of the function. To verify that your result is actually an inflection point, find the third derivative, which is the derivative of the second derivative of the original function. The third derivative is denoted as f ′ ′ ′ (x).
   • In the example above, the third derivative is:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Method 3 of 3: Part 3: Find the Inflection Point

1. 1 Check out the third derivative. The standard rule for estimating an inflection point is that if the third derivative is not zero (that is, f ′ ′ ′ (x) ≠ 0), then the inflection point is the true inflection point. Check out the third derivative; if it is not zero, then you have found the real inflection point.
   • In the example above, the third derivative is 6, not 0.So you've found the real inflection point.
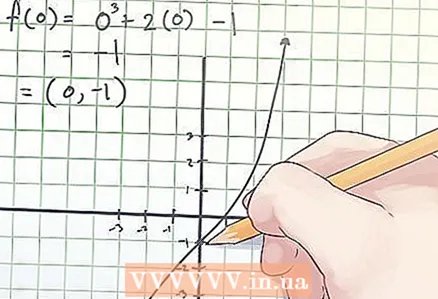2. 2 Find the coordinates of the inflection point. The inflection point coordinates are denoted as (x, f (x)), where x is the value of the independent variable "x" at the inflection point, f (x) is the value of the dependent variable "y" at the inflection point.
   • In the example above, when equating the second derivative to zero, you found that x = 0. So, to determine the coordinates of the inflection point, find f (0). Your calculation looks like this:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
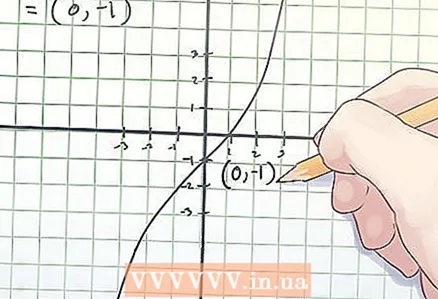3. 3 Write down the coordinates of the inflection point. The inflection point coordinates are the found x and f (x) values.
   • In the above example, the inflection point is at coordinates (0, -1).

Tips

• The first derivative of a free term (prime number) is always zero.