Author:
Randy Alexander
Date Of Creation:
3 April 2021
Update Date:
1 July 2024
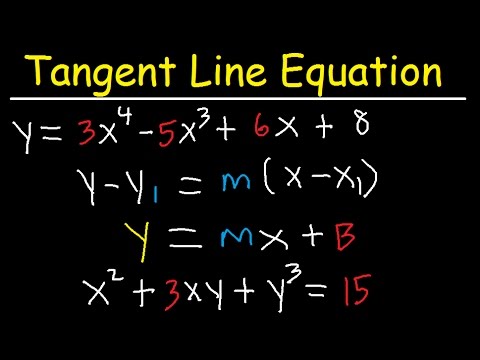
Content
Unlike a straight line, the coefficient of angle (slope) continuously changes as it moves along the curve. Calculus gives the idea that each point on the graph can be expressed as a coefficient of angle or "instantaneous rate of change". The tangent line at a point is a line that has the same angular coefficient and passes through the same point. To find a tangent line equation, you need to know how to derive the original equation.
Steps
Method 1 of 2: Find the equation for the tangent line
Graph functions and tangent lines (this step is optional, but recommended). The chart will help you more easily understand the problem and check if the answer is reasonable or not. Draw function graphs on grid paper, use the scientific calculator with graph function for reference if needed. Draw a tangent line through a given point (Remember that the tangent line passes through that point and has the same slope as the graph there).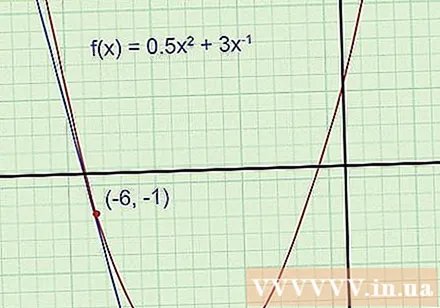
- Example 1: Parabolic drawing. Draw a tangent line through the point (-6, -1).
Even though you don't know the tangent equation, you can still see that its slope is negative and the intersection is negative (far below the parabolic vertex with the ordinate of -5.5). If the final answer found does not match these details, there must be an error in your calculation and you need to check again.
- Example 1: Parabolic drawing. Draw a tangent line through the point (-6, -1).

Get the first derivative to find the equation slope of the tangent line. With the function f (x), the first derivative f '(x) represents the equation for the slope of the tangent line at any point on f (x). There are many ways to take derivatives. Here is a simple example using the power rule:- Example 1 (cont.): The graph is given by a function.
Recalling the power rule when taking derivative :.
The first derivative of the function = f '(x) = (2) (0.5) x + 3 - 0.
f '(x) = x + 3. Replace x with any value a, the equation will give us the slope of the tangent line function f (x) at point x = a.
- Example 1 (cont.): The graph is given by a function.

Enter the x value of the point under consideration. Read the problem to find the coordinates of the point to find the tangent line. Enter the coordinate of this point in f '(x). The obtained result is the slope of the tangent line at the above point.- Example 1 (cont.): The point mentioned in the article is (-6, -1). Using diagonal -6 voltage into f '(x):
f '(- 6) = -6 + 3 = -3
The slope of the tangent line is -3.
- Example 1 (cont.): The point mentioned in the article is (-6, -1). Using diagonal -6 voltage into f '(x):
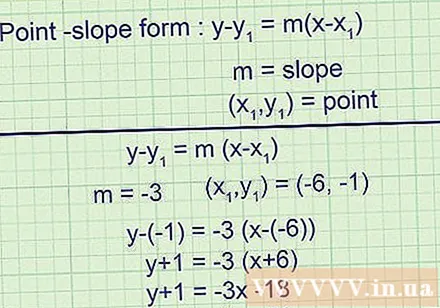
Write a tangent equation in the form of a straight line knowing the coefficient of the angle and a point on it. This linear equation is written as. Inside, m is the slope and is a point on the tangent line. You now have all the information you need to write a tangent equation in this form.- Example 1 (cont.):
The slope of the tangent line is -3, so:
The tangent line passes through the point (-6, -1), so the final equation is:
In short, we can:
- Example 1 (cont.):
Graphical confirmation. If you have a graphing calculator, plot the original function and the tangent line to check if the answer is correct. If doing calculations on paper, use graphs drawn earlier to make sure there are no obvious errors in your answer.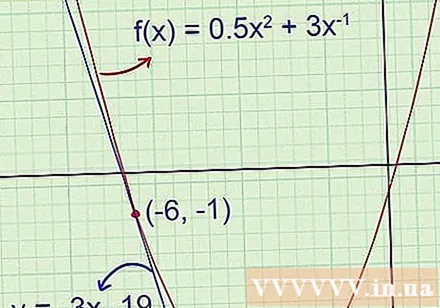
- Example 1 (cont.): The initial drawing shows that the tangent line has negative coefficients of angle and the offset is far below -5.5. The tangent equation just found is y = -3x -19, which means that -3 is the slope of the angle and -19 is the ordinate.
Try solving a more difficult problem. We go through all the steps above again.At this point, the goal is to find the tangent line of at x = 2: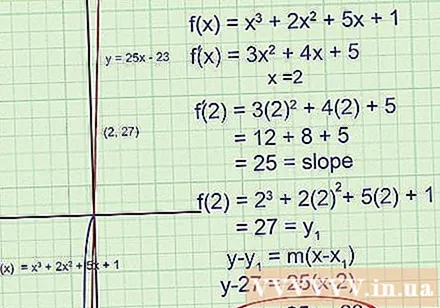
- Find the first derivative using the power rule:. This function will give us the slope of the tangent.
- For x = 2, find. This is the slope at x = 2.
- Note that this time, we don't have a point and only the x coordinate. To find the y coordinate, replace x = 2 in the original function:. The score is (2.27).
- Write an equation for a tangent line passing through a point and having the coefficient of the angle determined:
If necessary, reduce to y = 25x - 23.
Method 2 of 2: Solve related problems
Find the extreme on the graph. They are the points at which the graph approaches a local maximum (a point higher than neighboring points on both sides) or a local minimum (lower than neighboring points on both sides). The tangent line always has a zero coefficient at these points (a horizontal line). However, the coefficient of the angle is not enough to conclude that it is the extreme point. Here's how to find them: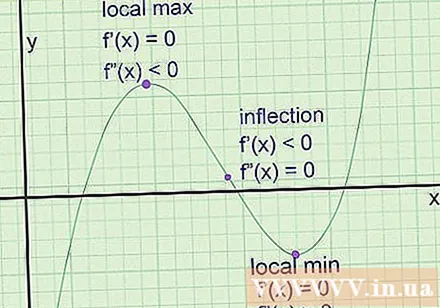
- Take the first derivative of the function to get f '(x), the slope of the slope of the tangent line.
- Solve the equation f '(x) = 0 to find the extreme point potential.
- Taking the quadratic derivative to get f '(x), the equation tells us the rate of change of the slope of the tangent line.
- At each potential extreme, change the coordinate a into f '' (x). If f '(a) is positive, we have a local minimum at a. If f '(a) is negative, we have a local maximum point. If f '(a) is 0, it will not be the extreme, it is an inflection point.
- If max or min reached at a, find f (a) to determine the intersection.
Find the equations of the normal. The "normal" line of a curve at a given point a passes through that point and is perpendicular to the tangent line. To find the equation for the normal, use the following: (slope of the normal) (slope of the normal) = -1 when they pass the same point on the graph. Specifically: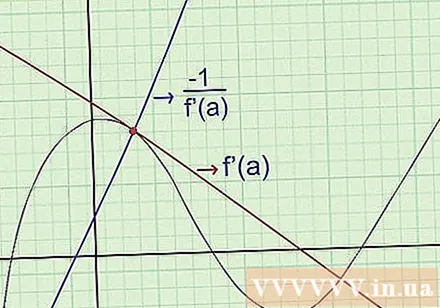
- Find f '(x), the slope of the tangent line.
- If at a given point, we have x = a: find f '(a) to determine the slope at that point.
- Calculate to find the coefficient of the normal.
- Write the equation for the perpendicular to knowing the coefficients of the angle and a point it passes through.
Advice
- If necessary, rewrite the original equation in standard form: f (x) = ... or y = ...