Content

• To step
• Tips

Synthetic division is an abbreviated method of dividing polynomials, where you divide the coefficients of the polynomials to remove variables and exponents. This allows you to work in the same way during this calculation as with a normal long division. To learn how to synthetically divide polynomials, follow the steps below.

To step

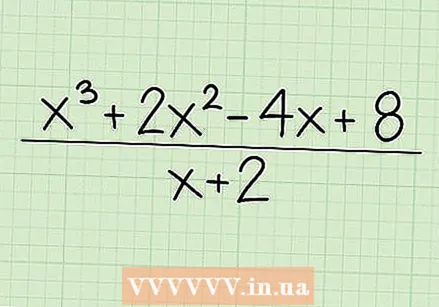1. Write down the problem. For example, you divide x + 2x - 4x + 8 by x + 2. Write the first quadratic equation, the dividend, in the numerator and write the second equation, the divisor, in the denominator.
2. Reverse the sign of the constant in the divisor. The constant in the divisor, x + 2, is positive so the inverse of the sign of the constant is -2.
3. Place this number outside the part outside the division sign. The division sign looks like a backward "L." Place the term -2 to the left of this symbol.
4. Write down all the coefficients of the dividend within the division sign. Write the terms from left to right as they appear. This looks like this: -2 | 1 2 -4 8.
5. Bring down the first coefficient. Place the first coefficient, 1, below itself. This looks like this:
   • -2| 1  2  -4  8
         ↓
         1
6. Multiply the first coefficient by the divisor and place it under the second coefficient. Multiply 1 by -2 and write the product -2 under the second term, 2. This looks like this:
   • -2| 1  2  -4  8
             -2
         1
7. Add the second coefficient and write the answer below the product. Now take the second coefficient, 2, and add it to -2. You write the result 0 under the two numbers, just like with long division. This is what it looks like:
   • -2| 1  2  -4  8
             -2
         1   0
8. Multiply the sum by the divisor and place the result under the third coefficient. Now take the sum, 0, and multiply it by the divisor, -2. Place the result 0 under 4, the third coefficient. This looks like this:
   • -2| 1  2  -4  8
             -2  0 
         1   
9. Add the product and the third coefficient and write the result under the product. Add 0 to -4 and write the answer -4 under 0. This is what it looks like:
   • -2| 1  2  -4  8
             -2   0 
         1   0   -4
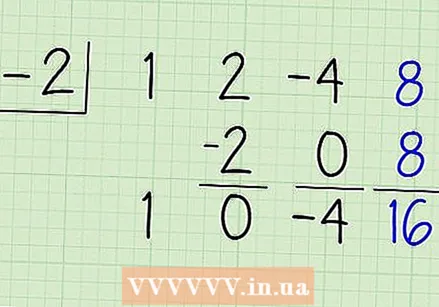10. Multiply this number by the divisor, write it under the last coefficient, and add it to the coefficient. Now multiply -4 by -2 and write the answer 8 under the fourth coefficient, 8, and add it to the fourth coefficient. 8 + 8 = 16, so this is your remainder. Write the number below the product. This is what this looks like:
    • -2| 1  2  -4  8
              -2   0   8
          1   0   -4   |16
11. Place each of the new coefficients next to a variable with a power that is 1 less than the original variables. In this case, the first sum is 1 and it is placed next to an x ​​to the second power (1 less than 3). The second sum, 0, is placed next to an x, but the result is 0, so this term can be dropped. And the third coefficient, -4, becomes a constant, a number with no variable, because the original variable was x. You can write an R next to 16, because this is the rest. This is what this will look like:
    • -2| 1  2  -4  8
              -2   0   8
          1   0   -4   |16
          X   + 0X - 4 R 16
      
      X - 4 R16
12. Write down the final answer. This is the new polynomial, x - 4, plus the remainder, 16 as the numerator and x + 2 as the denominator. This is what it looks like: x - 4 + 16 / (x +2).

Tips

• To check your answer, multiply the quotient by the divisor and add the remainder. This must be the same as the original polynomial.

  (divisor) (quotient) + (remainder)

  (X + 2)(X - 4) + 16

  Multiply by the outer first, inner last method.

  (X - 4X + 2X - 8) + 16

  X + 2X - 4X - 8 + 16

  X + 2X - 4X + 8