Content

• To step
• Method 1 of 4: Calculating work in joules
• Method 2 of 4: Calculating kinetic energy in joules
• Method 3 of 4: Calculating the Joule as electrical energy
• Method 4 of 4: Calculating the heat in joules
• Tips
• Warnings
• Necessities

The joule (J), named after the English physicist James Edward Joule, is one of the most important units of the International Metric System. The joule is used as a unit of work, energy and heat and is widely used in science. If you want your answer to be in joules, always use the standard scientific units.

To step

Method 1 of 4: Calculating work in joules

1. The definition of labor. Work is defined as a constant force applied to an object to move it a certain distance. If no more than one force is applied, it can be calculated as power X distance, and can be written in units of joules (equivalent to a "Newton meter"). In our first example, we take a person who wants to add a weight from the floor to chest height, and we calculate how much work that person has done.
   • The force must be applied in the direction of the movement. When holding an object and walking forward, no work is done on the object, because you are not pushing the object in the direction of its movement.
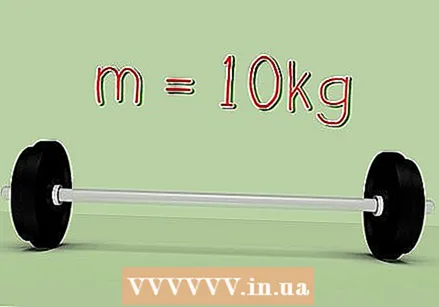2. Determine the mass of the object being moved. The mass of an object is needed to calculate the force required to move it. In our example we state that the weight has a mass of 10 kg.
   • Do not use pounds or other units that are not standard or the final answer will not be in joules.
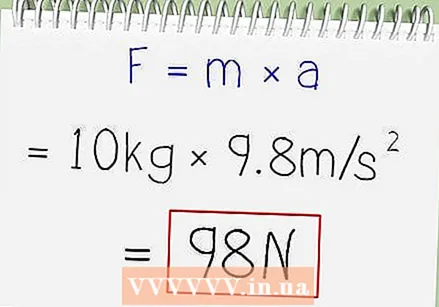3. Calculate the force. Force = mass x acceleration. In our example, lifting a weight straight up, acceleration we are trying to overcome is equal to gravity, 9.8 m / s downward. Calculate the force required to lift the weight using (10 kg) x (9.8 m / s) = 98 kg m / s = 98 Newtons (N).
   • If the object is moved horizontally, then gravity is irrelevant. Instead, the problem may prompt you to calculate the force required to overcome frictional resistance. If it is given what the acceleration of the object is when it is pushed, then you can multiply the given acceleration by the mass.
4. Measure the distance the object is being moved. In this example, we assume that the weight is lifted 1.5 meters (m). The distance must be measured in meters, otherwise the final answer cannot be recorded in Joules.
5. Multiply the force by the distance. To lift a weight of 98 Newton 1.5 meters, you will have to do 98 x 1.5 = 147 Joules of work.
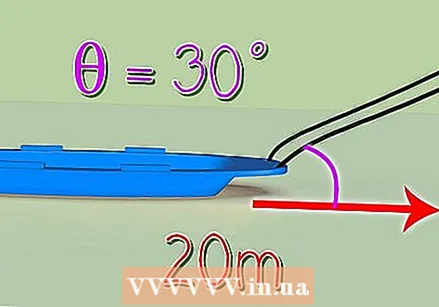6. Calculate labor for objects moving at an angle. Our example above was simple: someone applied an upward force on the object, and the object went up. Sometimes the direction of the force and the movement of the object are not quite the same, because multiple forces act on the object. In the following example we are going to calculate how many Joules it takes to drag a sled 25 meters through the snow by pulling a rope attached to the sled at an angle of 30º to the horizontal. The following holds: work = force x cos (θ) x distance. The θ symbol is the Greek letter "theta," and represents the angle between the direction of force and the direction of movement.
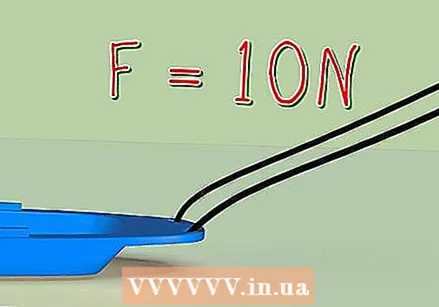7. Determine the total force applied. In this problem we say that someone pulls the rope with a force of 10 Newtons.
   • If a force "to the right," "up" or "in the direction of motion" has already been given, "force x cos (") "is as calculated, and you can proceed to multiply the values.
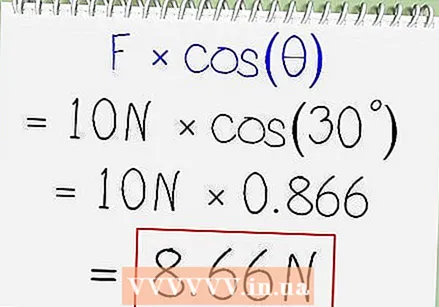8. Calculate the relevant force. Only part of the force pulls the carriage forward. Because the rope is up at an angle, the remaining force tries to lift the carriage up, counteracting gravity. Calculate the force in the direction of the movement:
   • In our example, the angle θ between the ground and the rope is 30º.
   • Calculate cos (θ). cos (30º) = (√3) / 2 = approximately 0.866. You can use a calculator to find this value, but make sure your calculator uses the correct unit as the one the angle is specified in (degrees or radians).
   • Multiply the total force x cos (θ). In our example, 10N x 0.866 = 8.66 N in the direction of motion.
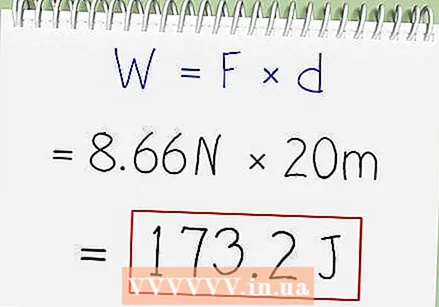9. Multiply force x distance. Now that we know how much force is being applied in the direction of the motion, we can calculate work as usual. Our problem tells us that the carriage has been towed 20 meters forward, so we calculate 8.66 N x 20 m = 173.2 joules of work.

Method 2 of 4: Calculating kinetic energy in joules

1. Understand some kinetic energy. Kinetic energy is the amount of energy in the form of movement. As with any form of energy, it can be expressed in Joules.
   • Kinetic energy is equal to the amount of work done to accelerate a stationary object to a certain speed. Once that speed is reached, the object retains that amount of kinetic energy until that energy is converted into heat (by friction), gravitational energy (by going against gravity), or other types of energy.
2. Determine the mass of the object. For example, we can measure the kinetic energy of a bicycle and a cyclist. Suppose the cyclist has a mass of 50 kg and the bicycle has a mass of 20 kg. That adds up to a total mass m of 70 kg. We can now treat them together as 1 object of 70 kg, because they move together at the same speed.
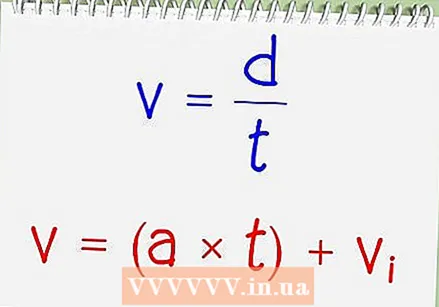3. Calculate the speed. If you already know the cyclist's speed or vector speed, write it down and move on. If you still need to calculate this, use one of the methods below. This concerns the speed, not the vector speed (which is the speed in a certain direction), even though the letter is often used as an abbreviation. v used for speed. Ignore any turns the cyclist makes and pretend that the entire distance is in a straight line.
   • If the cyclist is moving at a constant speed (no acceleration), measure the distance the cyclist traveled and divide by the number of seconds it took to cover that distance. This calculates the average speed, which in this scenario is the same as the speed at any given moment.
   • If the cyclist is moving at a constant acceleration and does not change direction, calculate his speed at the time t with the formula ’speed (time t) = (acceleration) (t) + initial speed. Time is in seconds, speed in meters / second and acceleration in m / s.
4. Enter the following numbers in the following formula. Kinetic energy = (1/2)m "v. For example, if the cyclist is moving at a speed of 15 m / s, then his kinetic energy is K = (1/2) (70 kg) (15 m / s) = (1/2) (70 kg) (15 m / s) (15 m / s) = 7875 kgm / s = 7875 newton meters = 7875 joules.
   • The formula for the kinetic energy can be derived from the definition of work, W = FΔs, and the equation v = v₀ + 2aΔs. Δs refers to "displacement," or also the distance traveled.

Method 3 of 4: Calculating the Joule as electrical energy

1. Calculate energy using power x time. Power is defined as the energy consumed per unit of time, so we can calculate the consumed energy by the power times the unit of time. This is useful when measuring power in watts, because 1 watt = 1 Joule / second. To find out how much energy a 60W incandescent bulb uses in 120 seconds, multiply the following: (60 watts) x (120 seconds) = 7200 joules.
   • This formula can be used for any kind of power, measured in watts, but electricity is the most obvious.
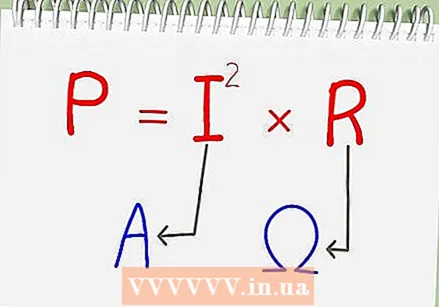2. Use the steps below to calculate the energy flow in an electrical circuit. The steps below are outlined as a practical example, but you can also use this method to understand theoretical physics problems. First, we calculate the power P using the formula P = I x R, where I is the current in amperes and R is the resistance in ohms. These units give us the power in watts, so from this point on we can apply the formula used in the previous step to calculate the energy in joules.
3. Choose a resistor. Resistors are indicated in ohms, with their value indicated directly on the resistor, or indicated by a series of colored rings. You can also test a resistance with an ohmmeter or multimeter. In this example, we assume that the resistance we are using is 10 ohms.
4. Connect the resistor to an energy source (battery). Use clamps for this or place the resistor in a test circuit.
5. Let a current flow through it for a certain amount of time. In this example we take 10 seconds as the time unit.
6. Measure the strength of the current. You do this with a flow meter or a multimeter. Most household current is in milliamps, so we assume that the current is 100 milliamps, or 0.1 amps.
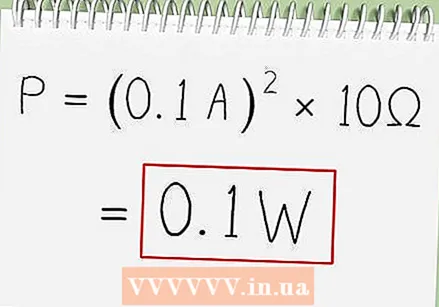7. Use the formula P = I x R. Now to find the power, you multiply the square power of the current by the resistance. This gives you the power of this circuit in watts. The square of 0.1 gives 0.01. Multiply this by 10, and you get an output power of 0.1 watts, or 100 milliwatts.
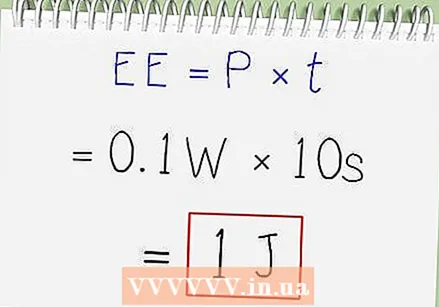8. Multiply the power by the elapsed time. This provides the energy in joules. 0.1 watts x 10 seconds equals 1 joule of electrical energy.
   • Because the Joule is a small unit and since the energy consumption of appliances is usually indicated in watts, milliwatts and kilowatts, it is often more convenient to calculate the number of kWh (kilowatt hours) consumed by a device. 1 watt equals 1 joule per second, or 1 joule equals 1 watt second; one kilowatt is equal to 1 kilojoule per second and one kilojoule is equal to 1 kilowatt second. There are 3,600 seconds in an hour, so 1 kilowatt-hour is equal to 3,600 kilowatt-seconds, 3,600 kilojoules, or 3,600,000 joules.

Method 4 of 4: Calculating the heat in joules

1. Determine the mass of the object to which heat is added. Use a balance or scales for this. If the object is a liquid, first weigh the empty container that the liquid will go into. You will have to subtract this from the mass of the container and liquid together to find the mass of the liquid. In this example we assume that the object is 500 grams of water.
   • Use grams, not another unit, otherwise the result will not be given in Joules.
2. Determine the specific heat of the object. This information can be found in binas chemistry reference books, but you can also find it online. This is the specific heat for water c equals 4.19 joules per gram for each degree Celsius - or 4.1855, if you want to be very precise.
   • Specific heat varies slightly depending on temperature and pressure. Different organizations and textbooks use different "standard temperatures," so you may find as much as 4,179 for the specific heat of water.
   • You can also use Kelvin instead of Celsius, because 1 degree is the same for both dishes (heating something with 3ºC is the same as with 3 Kelvin). Do not use Fahrenheit or the result will not be given in Joules.
3. Determine the current temperature of the object. If the object is a liquid, you can use a regular (mercury) thermometer. For other objects you may need a thermometer with a probe.
4. Heat the object and measure the temperature again. This allows you to measure the amount of heat that has been added to an object during heating.
   • If you want to know the total amount of energy stored in the form of heat, you can pretend that the initial temperature was absolute zero: 0 Kelvin or -273.15ºC.
5. Subtract the original temperature from the temperature after heating. This results in the change in the temperature of the object. Assuming that the water was initially 15 degrees Celsius and after heating it was 35 degrees Celsius, the change in temperature is therefore 20 degrees Celsius.
6. Multiply the object's mass by the specific heat and the change in temperature. You write this formula as H =mcΔT., where ΔT represents the "change in temperature". In this example, this becomes 500g x 4.19 x 20 = 41,900 joules.
   • Heat is generally expressed in calories or kilocalories. A calorie is defined as the amount of heat required to make 1 gram of water rise in temperature by 1 degree Celsius, while a kilocalorie (or Calorie) is the amount of heat required to raise the temperature of 1 kilogram of water by 1 degree Celsius. . In the example above, raising the temperature of 500 grams of water by 20 degrees Celsius requires 10,000 calories or 10 kilocalories.

Tips

• Related to the joule is another unit of work and energy called the erg; 1 erg equals 1 dyne force times a distance of 1 cm. One joule is equal to 10,000,000 erg.

Warnings

• Although the terms "joule" and "newton meter" refer to the same unit, in practice the "joule" is used to indicate any form of energy and for work performed in a straight line, as in the example of climbing stairs above. When used to calculate torque (force on a rotating object), we prefer the term "Newton meter".

Necessities

Calculating Work or Kinetic Energy:

• Stopwatch or timer
• Libra or balance
• Calculator with a cosine function (only for work, not always necessary)

Calculating electrical energy:

• Resistance
• Wires or a test board
• Multimeter (or an ohmmeter and a current meter)
• Fahnestock or alligator clips

Heat:

• Object to be heated
• Heat source (such as a Bunsen burner)
• Thermometer (a liquid thermometer or thermometer with a probe)
• Chemistry / chemistry reference (for finding the specific heat of the object being heated)