Content

• Steps
• Method 1 of 3: The Probability of a Single Random Event
• Method 2 of 3: Probability of Multiple Random Events
• Method 3 of 3: Converting Possibility into Probability
• Tips

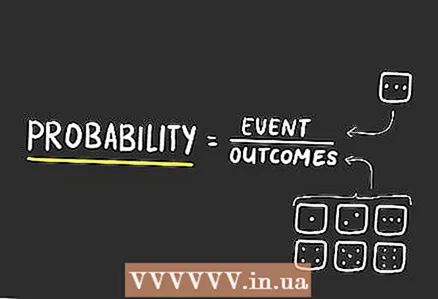
Probability shows the possibility of an event with a certain number of repetitions. This is the number of possible outcomes with one or more outcomes divided by the total number of possible events. The probability of several events is calculated by dividing the problem into individual probabilities and then multiplying these probabilities.

Steps

Method 1 of 3: The Probability of a Single Random Event

1. 1 Select an event with mutually exclusive outcomes. The probability can only be calculated if the event in question either occurs or does not occur. It is impossible to simultaneously receive any event and the opposite result. Examples of such events are the roll of a 5 on the game die or the victory of a particular horse in a race. Either five is rolled or not; a certain horse will either come first or not.

   For example: "It is impossible to calculate the probability of such an event: with one roll of the die, 5 and 6 will be rolled simultaneously.

   
   
2. 2 Identify all possible events and outcomes that may occur. Suppose you want to determine the probability that a 3 will be rolled on a 6-digit game die. Three of a kind is an event, and since we know that any of the 6 numbers can come up, the number of possible outcomes is six. Thus, we know that in this case there are 6 possible outcomes and one event, the probability of which we want to determine. Below are two more examples.
   • Example 1. What is the likelihood that you randomly pick a day that falls on the weekend? In this case, the event is "the choice of the day that falls on the weekend", and the number of possible outcomes is equal to the number of days of the week, that is, seven.
   • Example 2. The box contains 4 blue, 5 red and 11 white balls. If you take a random ball out of the box, what is the probability that it turns out to be red? The event is to "take out the red ball", and the number of possible outcomes is equal to the total number of balls, that is, twenty.
3. 3 Divide the number of events by the number of possible outcomes. This will determine the likelihood of a single event. If we consider a 3 on a die roll, the number of events is 1 (the 3 is on only one face of the die), and the total number of outcomes is 6. The result is a ratio of 1/6, 0.166, or 16.6%. The probability of an event for the two examples above is found as follows:
   • Example 1. What is the likelihood that you randomly pick a day that falls on the weekend? The number of events is 2, since there are two days off in one week, and the total number of outcomes is 7. So the probability is 2/7. The result obtained can also be written as 0.285 or 28.5%.
   • Example 2. The box contains 4 blue, 5 red and 11 white balls. If you take a random ball out of the box, what is the probability that it turns out to be red? The number of events is 5, since there are 5 red balls in the box, and the total number of outcomes is 20. Find the probability: 5/20 = 1/4. The result obtained can also be recorded as 0.25 or 25%.
4. 4 Add up the probabilities of all possible events and check if the sum is equal to 1. The total probability of all possible events should be 1, or 100%.If you fail 100%, chances are you made a mistake and missed one or more possible events. Check your calculations and make sure you factor in all the possible outcomes.
   • For example, the probability of a 3 being rolled on a die roll is 1/6. In this case, the probability of falling out of any other digit out of the remaining five is also 1/6. As a result, we get 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6, that is, 100%.
   • If you, for example, forget about the number 4 on the die, adding the probabilities will give you only 5/6, or 83%, which is not equal to one and indicates an error.
5. 5 Imagine the probability of an impossible outcome as 0. This means that this event cannot happen, and its probability is 0. Thus, you can take into account impossible events.
   • For example, if you were to calculate the probability that Easter falls on Monday in 2020, you would get 0 because Easter is always celebrated on Sunday.

Method 2 of 3: Probability of Multiple Random Events

1. 1 When considering independent events, calculate each probability separately. Once you determine what the probabilities of events are, they can be calculated separately. Suppose you want to know the probability that when you roll the dice twice in a row, 5. We know that the probability of getting one five is 1/6, and the probability of getting the second five is also 1/6. The first outcome is not related to the second.
   • Several hits of fives are called independent events, since what is rolled the first time does not affect the second event.
2. 2 Consider the impact of previous outcomes when calculating the probability for dependent events. If the first event affects the probability of the second outcome, they talk about calculating the probability dependent events... For example, if you choose two cards from a deck of 52 cards, after drawing the first card, the composition of the deck changes, which affects the choice of the second card. To calculate the probability of the second of two dependent events, subtract 1 from the number of possible outcomes when calculating the probability of the second event.
   • Example 1... Consider the following event: Two cards are drawn from the deck at random one after the other. What is the likelihood that both cards will be of clubs? The probability that the first card will have a club suit is 13/52, or 1/4, since there are 13 cards of the same suit in the deck.
     • After that, the probability that the second card will be of clubs is 12/51, since there is no longer one card of clubs. This is because the first event affects the second. If you draw a three of clubs and don't put it back, there will be one less card in the deck (51 instead of 52).
   • Example 2. The box contains 4 blue, 5 red and 11 white balls. If you pick three balls at random, what is the probability that the first will be red, the second blue, and the third white?
     • The probability that the first ball is red is 5/20, or 1/4. The probability that the second ball will be blue is 4/19, since there is one less ball left in the box, but still 4 blue ball. Finally, the probability that the third ball will turn out to be white is 11/18, since we have already drawn two balls.
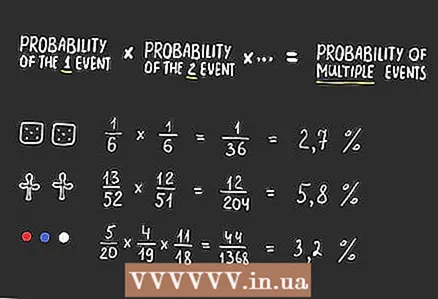3. 3 Multiply the probabilities of each individual event. Regardless of whether you are dealing with independent or dependent events, as well as the number of outcomes (there can be 2, 3, or even 10), you can calculate the overall probability by multiplying the probabilities of all the events in question by each other. As a result, you will get the probability of several events following one by one... For example, the task is Find the probability that when rolling the dice twice in a row, 5... These are two independent events, the probability of each of which is 1/6. Thus, the probability of both events is 1/6 x 1/6 = 1/36, that is, 0.027, or 2.7%.
   • Example 1. Two cards are drawn from the deck at random one after the other.What is the likelihood that both cards will be of clubs? The probability of the first event is 13/52. The probability of the second event is 12/51. Find the overall probability: 13/52 x 12/51 = 12/204 = 1/17, which is 0.058, or 5.8%.
   • Example 2. The box contains 4 blue, 5 red and 11 white balls. If you draw three balls at random from the box one by one, what is the probability that the first will turn out to be red, the second blue, and the third white? The probability of the first event is 5/20. The probability of the second event is 4/19. The probability of the third event is 11/18. So the overall probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032, or 3.2%.

Method 3 of 3: Converting Possibility into Probability

1. 1 Think of the opportunity as a positive fraction in the numerator. Let's go back to our example with colored balls. Suppose you want to know the probability that you will get a white ball (there are 11 in total) from the whole set of balls (20). The chance that a given event will occur is equal to the ratio of the probability that it will happen, to the probability that it not will happen. Since there are 11 white balls in the box and 9 balls of a different color, the ability to draw a white ball is equal to a ratio of 11: 9.
   • The number 11 represents the probability of hitting a white ball, and the number 9 is the probability of drawing a ball of a different color.
   • Thus, it is more likely that you will get the white ball.
2. 2 Add these values ​​together to convert possibility to probability. Converting an opportunity is pretty straightforward. First, it should be split into two separate events: the chance to draw a white ball (11) and the chance to draw a ball of a different color (9). Add up the numbers to find the total number of possible events. Write everything down as a probability with the total number of possible outcomes in the denominator.
   • You can take out a white ball in 11 ways, and a ball of a different color in 9 ways. Thus, the total number of events is 11 + 9, that is, 20.
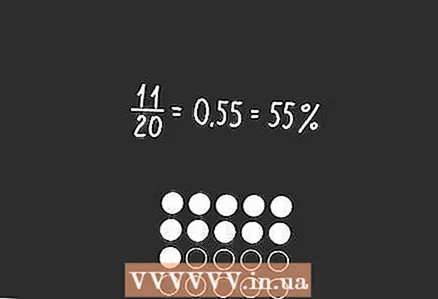3. 3 Find the opportunity as if you were calculating the probability of one event. As we have already determined, there are 20 possibilities in total, and in 11 cases you can get a white ball. Thus, the probability of drawing out a white ball can be calculated in the same way as the probability of any other single event. Divide 11 (the number of positive outcomes) by 20 (the number of all possible events) and you will determine the probability.
   • In our example, the probability of hitting the white ball is 11/20. As a result, we get 11/20 = 0.55, or 55%.

Tips

• Mathematicians usually use the term "relative probability" to describe the likelihood that an event will occur. The definition "relative" means that the result is not 100% guaranteed. For example, if you flip a coin 100 times, then, probably, exactly 50 heads and 50 tails will not be dropped. The relative likelihood takes this into account.
• The probability of any event cannot be negative. If you get a negative value, check your calculations.
• Most often, probabilities are written as fractions, decimals, percentages, or on a scale of 1-10.
• You may find it useful to know that in sports and bookmaking betting odds are expressed as odds against, which means that the possibility of a claimed event is ranked first and the odds of an event that is not expected are ranked second. While this can be confusing, it is important to keep this in mind if you are going to bet on any sporting event.