Content

• Steps
• Part 1 of 4: How to Write an Equation
• Part 2 of 4: How to write Euclid's algorithm
• Part 3 of 4: How to Find a Solution Using Euclid's Algorithm
• Part 4 of 4: Find Infinite Other Solutions

To solve a linear Diophantine equation, you need to find the values ​​of the variables "x" and "y", which are integers. An integer solution is more complicated than usual and requires a specific set of actions. First, you need to calculate the greatest common divisor (GCD) of the coefficients, and then find a solution. Once you've found one integer solution to a linear equation, you can use a simple pattern to find an infinite number of other solutions.

Steps

Part 1 of 4: How to Write an Equation

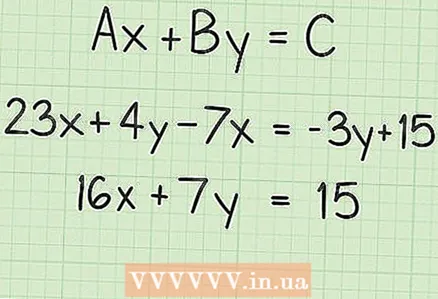1. 1 Write the equation down in standard form. A linear equation is an equation in which the exponents of the variables do not exceed 1. To solve such a linear equation, first write it in standard form. The standard form of a linear equation looks like this: ${ displaystyle Ax + By = C}$, where ${ displaystyle A, B}$ and ${ displaystyle C}$ - whole numbers.
   • If the equation is given in a different form, bring it to standard form using basic algebraic operations. For example, given the equation ${ displaystyle 23x + 4y-7x = -3y + 15}$... Give similar terms and write the equation like this: ${ displaystyle 16x + 7y = 15}$.
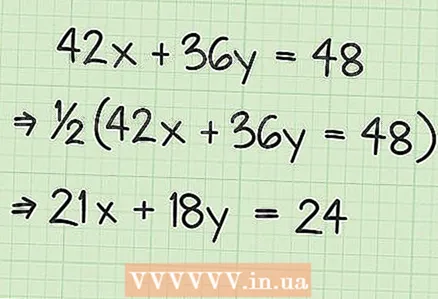2. 2 Simplify the equation (if possible). When you write the equation in standard form, look at the coefficients ${ displaystyle A, B}$ and ${ displaystyle C}$... If these odds have a GCD, divide all three odds by it. The solution to such a simplified equation will also be the solution to the original equation.
   • For example, if all three coefficients are even, divide them by at least 2. For example:
     • ${ displaystyle 42x + 36y = 48}$ (all members are divisible by 2)
     • ${ displaystyle 21x + 18y = 24}$ (now all members are divisible by 3)
     • ${ displaystyle 7x + 6y = 8}$ (this equation can no longer be simplified)
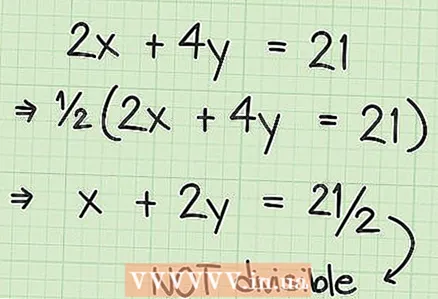3. 3 Check if the equation can be solved. In some cases, you can immediately state that the equation has no solutions. If the coefficient "C" is not divisible by the GCD of the coefficients "A" and "B", the equation has no solutions.
   • For example, if both coefficients ${ displaystyle A}$ and ${ displaystyle B}$ are even, then the coefficient ${ displaystyle C}$ must be even. But if ${ displaystyle C}$ odd, then there is no solution.
     • The equation ${ displaystyle 2x + 4y = 21}$ no integer solutions.
     • The equation ${ displaystyle 5x + 10y = 17}$ there are no integer solutions since the left side of the equation is divisible by 5 and the right side is not.

Part 2 of 4: How to write Euclid's algorithm

1. 1 Understand Euclid's algorithm. It is a series of repeated divisions in which the previous remainder is used as the next divisor. The last divisor that divides the numbers integrally is the greatest common divisor (GCD) of the two numbers.
   • For example, let's find the GCD of numbers 272 and 36 using Euclid's algorithm:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Divide the larger number (272) by the smaller one (36) and pay attention to the remainder (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - divide the previous divisor (36) by the previous remainder (20). Note the new residue (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - divide the previous divisor (20) by the previous remainder (16). Note the new residue (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Divide the previous divisor (16) by the previous remainder (4). Since the remainder is 0, we can say that 4 is the GCD of the original two numbers 272 and 36.
2. 2 Apply Euclid's algorithm to the coefficients "A" and "B". When you write the linear equation in standard form, determine the coefficients "A" and "B" and then apply the Euclidean algorithm to them to find the GCD. For example, given a linear equation ${ displaystyle 87x-64y = 3}$.
   • Here is Euclid's algorithm for coefficients A = 87 and B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
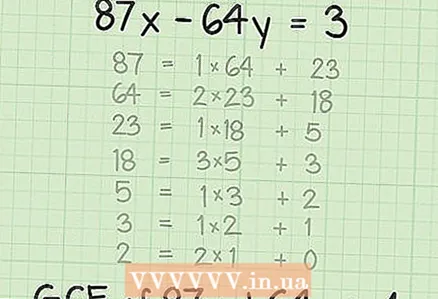3. 3 Find the Greatest Common Factor (GCD). Since the last divisor was the number 1, the gcd 87 and 64 are 1. Thus, 87 and 64 are prime numbers relative to each other.
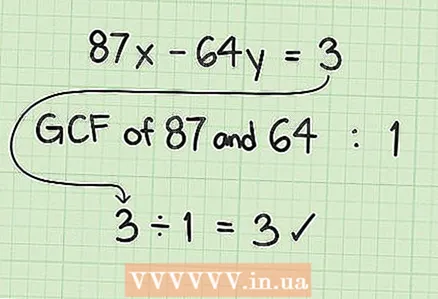4. 4 Analyze the result. When you find the gcd coefficients ${ displaystyle A}$ and ${ displaystyle B}$, compare it with the coefficient ${ displaystyle C}$ the original equation. If ${ displaystyle C}$ divisible by gcd ${ displaystyle A}$ and ${ displaystyle B}$, the equation has an integer solution; otherwise the equation has no solutions.
   • For example, the equation ${ displaystyle 87x-64y = 3}$ can be solved because 3 is divisible by 1 (gcd = 1).
   • For example, suppose GCD = 5. 3 is not evenly divisible by 5, so this equation has no integer solutions.
   • As shown below, if an equation has one integer solution, it also has an infinite number of other integer solutions.

Part 3 of 4: How to Find a Solution Using Euclid's Algorithm

1. 1 Number the steps for calculating GCD. To find the solution to a linear equation, you need to use the Euclidean algorithm as the basis for the substitution and simplification process.
   • Start by numbering the steps for calculating the GCD. The calculation process looks like this:
     • ${ displaystyle { text {Step 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Step 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Step 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Step 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Step 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Step 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Step 7}}: 2 = (2 * 1) +0}$
2. 2 Pay attention to the last step, where there is a remainder. Rewrite the equation for this step to isolate the remainder.
   • In our example, the last step with remainder is step 6. The remainder is 1. Rewrite the equation in step 6 as follows:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Isolate the remainder of the previous step. This process is a step-by-step "move up". Each time you will isolate the remainder in the equation in the previous step.
   • Isolate the remainder of the equation in Step 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ or ${ displaystyle 2 = 5-3}$
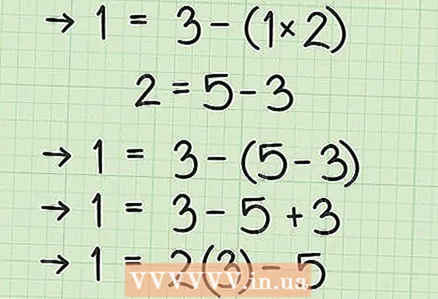4. 4 Substitute and simplify. Notice that the equation in Step 6 contains the number 2, and in the equation in Step 5, the number 2 is isolated. So instead of “2” in the equation in step 6, substitute the expression in step 5:
   • ${ displaystyle 1 = 3-2}$ (equation of step 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (instead of 2, an expression was substituted)
   • ${ displaystyle 1 = 3-5 + 3}$ (opened brackets)
   • ${ displaystyle 1 = 2 (3) -5}$ (simplified)
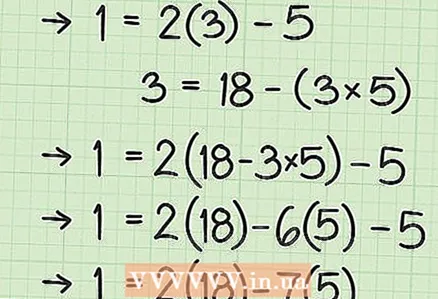5. 5 Repeat the substitution and simplification process. Repeat the described process, moving through the Euclidean algorithm in reverse order. Each time you will rewrite the equation from the previous step and plug it into the last equation you get.
   • The last step we looked at was step 5. So go to step 4 and isolate the remainder in the equation for that step:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Substitute this expression for "3" in the last equation:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Continue with the substitution and simplification process. This process will be repeated until you reach the initial step of the Euclidean algorithm. The goal of the process is to write the equation with the coefficients 87 and 64 of the original equation to be solved. In our example:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (substituted the expression from step 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (substituted the expression from step 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (substituted the expression from step 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Rewrite the resulting equation in accordance with the original coefficients. When you return to the first step of the Euclidean algorithm, you will see that the resulting equation contains two coefficients of the original equation. Rewrite the equation so that the order of its terms matches the coefficients of the original equation.
   • In our example, the original equation ${ displaystyle 87x-64y = 3}$... Therefore, rewrite the resulting equation so that the coefficients are brought into line.Pay special attention to the coefficient "64". In the original equation, this coefficient is negative, and in the Euclidean algorithm, it is positive. Therefore, the factor 34 must be made negative. The final equation will be written like this:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
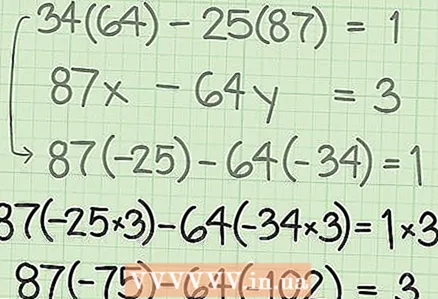8. 8 Apply the appropriate multiplier to find a solution. Note that in our example, GCD = 1, so the final equation is 1. But the original equation (87x-64y) is 3. Therefore, all terms in the final equation must be multiplied by 3 to get the solution:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
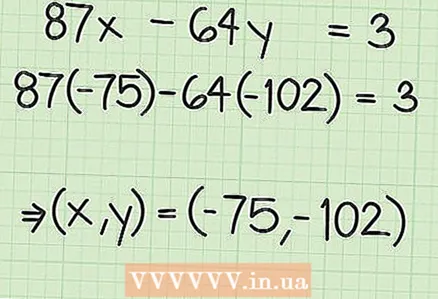9. 9 Write down the integer solution to the equation. The numbers that are multiplied by the coefficients of the original equation are the solutions to that equation.
   • In our example, write the solution as a pair of coordinates: ${ displaystyle (x, y) = (- 75, -102)}$.

Part 4 of 4: Find Infinite Other Solutions

1. 1 Understand that there are an infinite number of solutions. If a linear equation has one integer solution, then it must have an infinite number of integer solutions. Here's a quick proof (in algebraic form):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (if you add "B" to "x" and subtract "A" from "y", the value of the original equation will not change)
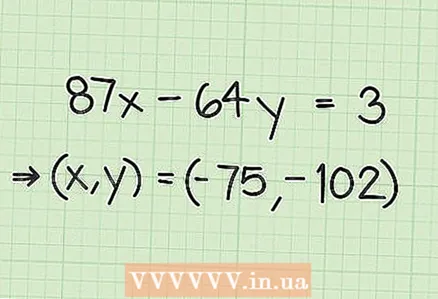2. 2 Record the original x and y values. The template for calculating the next (infinite) solutions starts with the only solution you've already found.
   • In our example, the solution is a pair of coordinates ${ displaystyle (x, y) = (- 75, -102)}$.
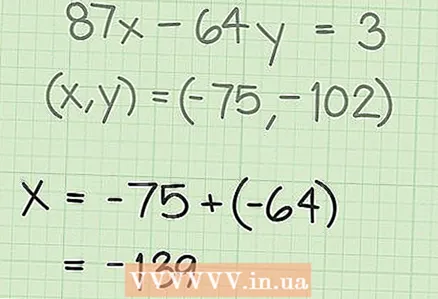3. 3 Add the "B" factor to the "x" value. Do this to find the new x value.
   • In our example, x = -75, and B = -64:
     • ${ displaystyle x = -75 + (- 64) = - 139}$
   • Thus, the new value "x": x = -139.
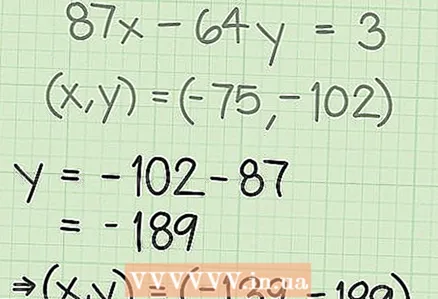4. 4 Subtract the "A" factor from the "y" value. So that the value of the original equation does not change, when adding one number to "x", you need to subtract another number from "y".
   • In our example, y = -102, and A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Thus, the new value for "y": y = -189.
   • The new pair of coordinates will be written like this: ${ displaystyle (x, y) = (- 139, -189)}$.
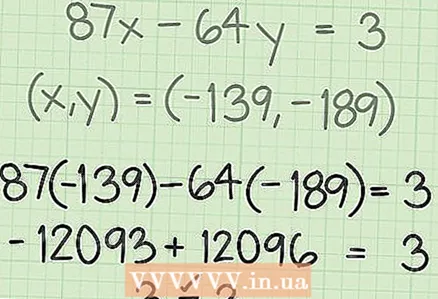5. 5 Check the solution. To verify that the new coordinate pair is a solution to the original equation, plug the values ​​into the equation.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Since the equality is met, the decision is correct.
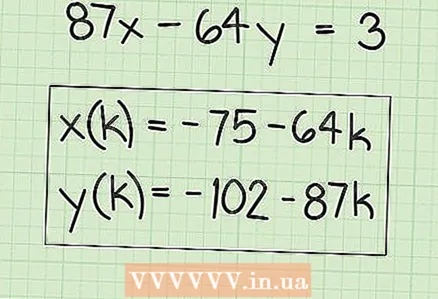6. 6 Write down expressions to find many solutions. The "x" values ​​will equal the original solution plus any multiple of the "B" factor. This can be written as the following expression:
   • x (k) = x + k (B), where “x (k)” is the set of “x” values ​​and “x” is the original (first) value of “x” that you found.
     • In our example:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), where y (k) is the set of y values ​​and y is the original (first) y value that you found.
     • In our example:
     • ${ displaystyle y (k) = - 102-87k}$