Content

• Steps
• Method 1 of 4: Enumerating multiples
• Method 2 of 4: Using Greatest Common Divisor
• Method 3 of 4: Prime Each Denominator
• Method 4 of 4: Working with Mixed Numbers
• What do you need

To add or subtract fractions with different denominators (numbers below the fractional bar), you first need to find their lowest common denominator (LCM). This number will be the smallest multiple that occurs in the list of multiples of each denominator, that is, a number that is evenly divisible by each denominator. You can also calculate the least common multiple (LCM) of two or more denominators. In any case, we are talking about integers, the methods of finding which are very similar. Once you've identified the NOZ, you can bring the fractions to a common denominator, which in turn allows you to add and subtract them.

Steps

Method 1 of 4: Enumerating multiples

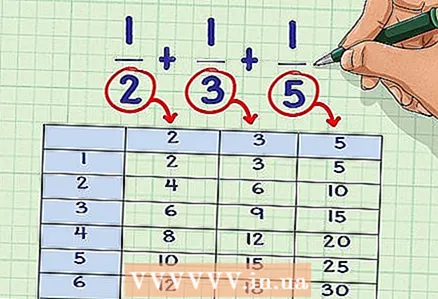1. 1 List the multiples of each denominator. List multiple multiples for each denominator in the equation. Each list should consist of the product of the denominator by 1, 2, 3, 4, and so on.
   • Example: 1/2 + 1/3 + 1/5
   • Multiples of 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; etc.
   • Multiples of 3: 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; etc.
   • Multiples of 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; etc.
2. 2 Find the least common multiple. Go through each list and note any multiples that are common to all denominators. After identifying the common multiples, determine the lowest denominator.
   • Note that if no common denominator is found, you may need to continue writing out the multiples until the common multiple appears.
   • It is better (and easier) to use this method when the denominators are small.
   • In our example, the common multiple of all denominators is 30: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
   • NOZ = 30
3. 3 Rewrite the original equation. In order to bring the fractions to a common denominator without changing their value, multiply each numerator (the number above the fractional bar) by the number equal to the quotient of dividing the NOZ by the corresponding denominator.
   • Example: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
   • New equation: 15/30 + 10/30 + 6/30
4. 4 Solve the resulting equation. After finding the NOZ and changing the corresponding fractions, simply solve the resulting equation. Remember to simplify your answer (if possible).
   • Example: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30

Method 2 of 4: Using Greatest Common Divisor

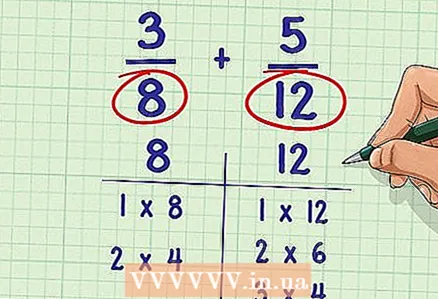1. 1 List the divisors of each denominator. A divisor is an integer that evenly divides the given number. For example, the divisors of the number 6 are the numbers 6, 3, 2, 1. The divisor of any number is 1, because any number is divisible by one.
   • Example: 3/8 + 5/12
   • Divisors 8: 1, 2, 4, 8
   • Divisors of 12: 1, 2, 3, 4, 6, 12
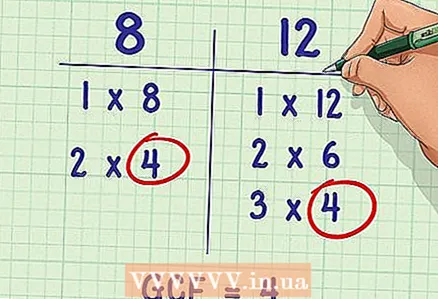2. 2 Find the greatest common factor (GCD) of both denominators. After listing the divisors of each denominator, mark all common factors. The largest common factor is the greatest common factor you will need to solve the problem.
   • In our example, the common factors for the denominators 8 and 12 are the numbers 1, 2, 4.
   • GCD = 4.
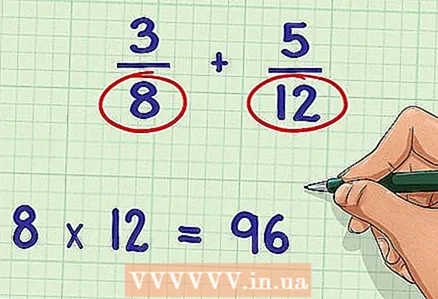3. 3 Multiply the denominators together. If you want to use GCD to solve a problem, first multiply the denominators together.
   • Example: 8 * 12 = 96
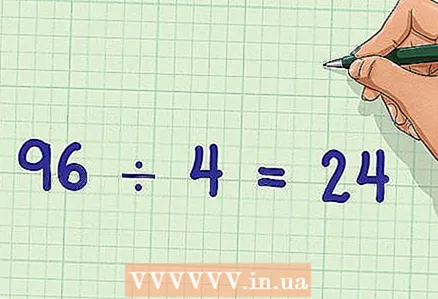4. 4 Divide the resulting value by the GCD. Having received the result of multiplying the denominators, divide it by the GCD you calculated. The resulting number will be the lowest common denominator (LCN).
   • Example: 96/4 = 24
5. 5 Divide the NOZ by the original denominator. To calculate the factor that is required to bring the fractions to a common denominator, divide the NOZ you found by the original denominator. Multiply the numerator and denominator of each fraction by this factor. You will get fractions with a common denominator.
   • Example: 24/8 = 3; 24/12 = 2
   • (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
   • 9/24 + 10/24
6. 6 Solve the resulting equation. NOZ found; now you can add or subtract fractions. Remember to simplify your answer (if possible).
   • Example: 9/24 + 10/24 = 19/24

Method 3 of 4: Prime Each Denominator

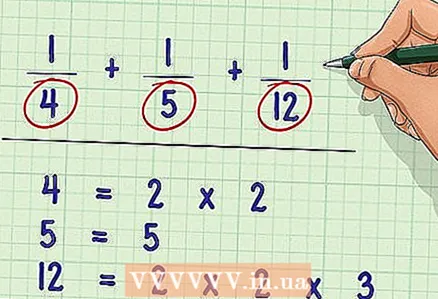1. 1 Factor each denominator. Divide each denominator into prime factors, that is, the prime numbers that, when multiplied, give the original denominator. Recall that prime factors are numbers that are divisible only by 1 or themselves.
   • Example: 1/4 + 1/5 + 1/12
   • Prime factors of 4: 2 * 2
   • Prime factors of 5: 5
   • Prime factors of 12: 2 * 2 * 3
2. 2 Count the number of times each prime factor each denominator has. That is, determine how many times each prime factor appears in the list of factors for each denominator.
   • Example: There are two 2 for the denominator 4; zero 2 for 5; two 2 for 12
   • There is zero 3 for 4 and 5; one 3 for 12
   • There is zero 5 for 4 and 12; one 5 for 5
3. 3 Take only the largest number of times for each prime factor. Determine the largest number of times each prime factor appears in any denominator.
   • For example: the largest number of times for a multiplier 2 - 2 times; for 3 - 1 time; for 5 - 1 time.
4. 4 Write down the prime factors found in the previous step in order. Do not write down the number of times each prime factor appears in all of the original denominators - do it counting as many times as possible (as described in the previous step).
   • Example: 2, 2, 3, 5
5. 5 Multiply these numbers. The product of these numbers is NOZ.
   • Example: 2 * 2 * 3 * 5 = 60
   • NOZ = 60
6. 6 Divide the NOZ by the original denominator. To calculate the factor that is required to bring the fractions to a common denominator, divide the NOZ you found by the original denominator. Multiply the numerator and denominator of each fraction by this factor. You will get fractions with a common denominator.
   • Example: 60/4 = 15; 60/5 = 12; 60/12 = 5
   • 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
   • 15/60 + 12/60 + 5/60
7. 7 Solve the resulting equation. NOZ found; now you can add or subtract fractions. Remember to simplify your answer (if possible).
   • Example: 15/60 + 12/60 + 5/60 = 32/60 = 8/15

Method 4 of 4: Working with Mixed Numbers

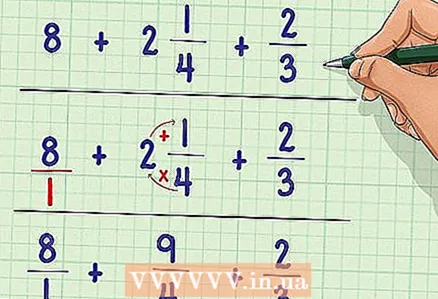1. 1 Convert each mixed number to an improper fraction. To do this, multiply the whole part of the mixed number by the denominator and add with the numerator - this will be the numerator of the improper fraction. Convert an integer to a fraction too (just put 1 in the denominator).
   • Example: 8 + 2 1/4 + 2/3
   • 8 = 8/1
   • 2 1/4, 2 * 4 + 1 = 8 + 1 = 9; 9/4
   • Rewritten equation: 8/1 + 9/4 + 2/3
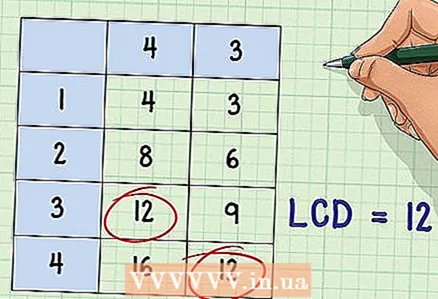2. 2 Find the lowest common denominator. Calculate the NOZ in any way described in the previous sections. For this example, we will use the multiples enumeration method, in which the multiples of each denominator are written out and based on which the NCD is calculated.
   • Note that you do not need to list multiples for 1since any number multiplied by 1, equal to himself; in other words, each number is a multiple 1.
   • Example: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; etc.
   • 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; etc.
   • NOZ = 12
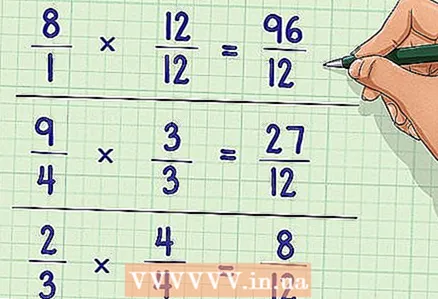3. 3 Rewrite the original equation. Multiply the numerators and denominators of the original fractions by a number equal to the quotient of the NOZ divided by the corresponding denominator.
   • For example: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
   • 96/12 + 27/12 + 8/12
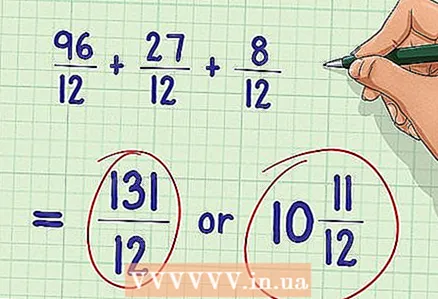4. 4 Solve the equation. NOZ found; now you can add or subtract fractions. Remember to simplify your answer (if possible).
   • Example: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12

What do you need

• Pencil
• Paper
• Calculator (optional)