Content

• Steps
• Advice

Have you ever left a bottle of water in the sun for a few hours, then opened the lid and heard a small "pop"? This sound is due vapor pressure in the cause bottle. In chemistry, vapor pressure is the pressure acting on the wall of a closed vessel as the liquid in the vessel evaporates (turns into a gas). To find the vapor pressure at a known temperature use the Clausius-Clapeyron equation: ln (P1 / P2) = (ΔH_vap/ R) ((1 / T2) - (1 / T1)).

Steps

Method 1 of 3: Use the Clausius-Clapeyron equation

1. 

   Write the Clausius-Clapeyron equation. When considering the change in vapor pressure over time, the formula for calculating vapor pressure is the Clausius-Clapeyron equation (named after physicists Rudolf Clausius and Benoît Paul Émile Clapeyron). This is a commonly used formula to solve common vapor pressure problems in physics and chemistry. The formula is written as follows: ln (P1 / P2) = (ΔH_vap/ R) ((1 / T2) - (1 / T1)). In this formula, the variables represent: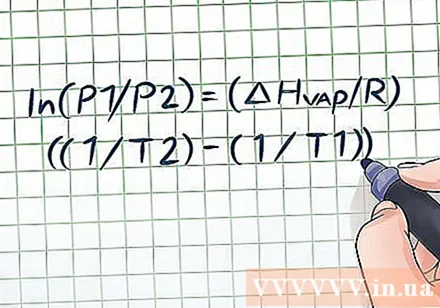
   • ΔH_vap: Evaporation enthalpy of liquids. This value can be found in the table at the end of a chemistry textbook.
   • R: Ideal gas constant and equal to 8,314 J / (K × Mol).
   • T1: Temperature at which the vapor pressure is known (initial temperature).
   • T2: The temperature at which the vapor pressure is required (final temperature).
   • P1 and P2: The corresponding vapor pressure at temperatures T1 and T2.

2. 

   
   
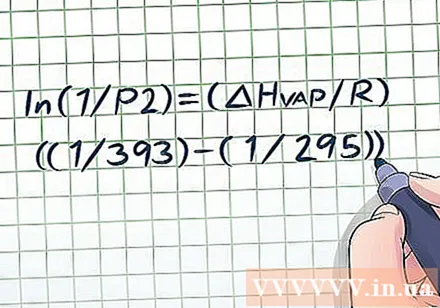
   Substitute known values ​​for variables. The Clausius-Clapeyron equation looks quite complicated because there are many different variables, but it is not too difficult if the problem provides enough information. The most basic steam pressure problems will give you two values ​​of temperature and one value of pressure or two values ​​of pressure and one value of temperature - once you have these data it's easy to solve.
   • For example, suppose the problem is for a container of liquid at 295 K and with a vapor pressure of 1 atmosphere (atm). The question is: What is the steam pressure at a temperature of 393 K? We have two values ​​for temperature and one for pressure, so it is possible to solve for the remaining pressure using the Clausius-Clapeyron equation. Putting values ​​into variables, we have ln (1 / P2) = (ΔH_vap/ R) ((1/393) - (1/295)).
   • For the Clausius-Clapeyron equation, we must always use a temperature value Kelvin. You can use any pressure value, as long as it is in the same units for both P1 and P2.

3. 

   
   
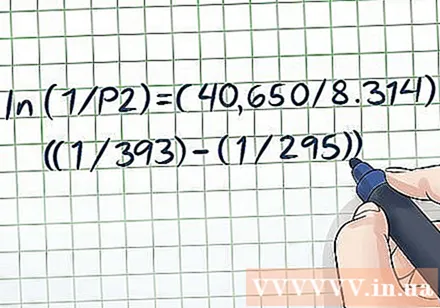
   Replace the constants. The Clausius-Clapeyron equation has two constants: R and ΔH_vap. R is always equal to 8,314 J / (K × Mol). However, ΔH_vap (volatile enthalpy) depends on the type of vaporizing liquid given by the problem. With that said, you can look up ΔH values_vap of a variety of substances at the end of a chemistry or physics textbook, or look it up online (eg here.)
   • In the example above, assume the liquid is pure water. If look up in the table value H_vap, we have ΔH_vap of purified water is approximately 40.65 kJ / mol. Since the H value uses joul units, we have to convert it to 40,650 J / mol.
   • Putting constants into the equation, we have ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295)).

4. 

   
   
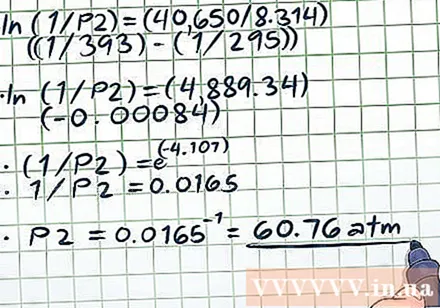
   Solve the equation. After you have inserted all of the values ​​into the variables of the equation, except for the variable we are calculating, continue solving the equation according to the usual algebraic principle.
   • The hardest point when solving the equation (ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295))) is the processing of the natural logarithmic function (ln). To eliminate the natural log function, use both sides of the equation as the exponent of the mathematical constant e. In other words, ln (x) = 2 → e = e → x = e.
   • Now let's solve the example's equation:
   • ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295))
   • ln (1 / P2) = (4,889.34) (- 0.00084)
   • (1 / P2) = e
   • 1 / P2 = 0.0165
   • P2 = 0.0165 = 60.76 atm. This value is reasonable - in a closed vessel, when the temperature is increased by almost 100 degrees (to a temperature approximately 20 degrees above the boiling point of water) there is a lot of steam generated, so the pressure will increase. much.
   advertisement

Method 2 of 3: Find the vapor pressure of the dissolved solution

1. 

   Write Raoult's Law. In reality, we rarely work with pure liquids - often we have to work with mixtures of many different substances. Some common mixes are created by dissolving a small amount of a chemical called solute in a large amount of other chemicals called Solvent to form solution. In this case, we need to know the equation for Raoult's Law (named after physicist François-Marie Raoult), which looks like this: P_solution= P_SolventX_Solvent. In this formula, the variables represent: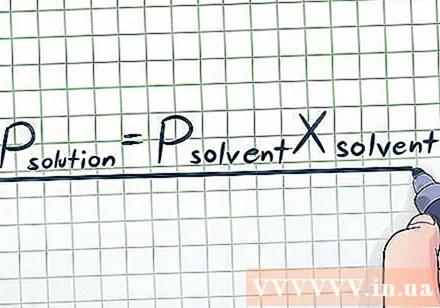
   • P_solution: Vapor pressure of all solution (all solution components)
   • P_Solvent: Solvent vapor pressure
   • X_Solvent: Molar fraction of the solvent.
   • Don't worry if you don't already know the term "molar part" - we'll explain it in the next steps.

2. 

   Distinguish solvents and solvents in solution. Before you calculate the vapor pressure of a solution, you need to identify the substances that are given by the problem. Note that a solution is formed when a solvent is dissolved in a solvent - the chemical that is dissolved is always a solute, and the chemical that does the job is the solvent.
   • In this section we will take a simple example to illustrate the above concepts. Suppose we want to find the vapor pressure of the syrup solution. Usually syrup is prepared from one part sugar dissolved in one part water, hence we say sugar is solute and water is solvent.
   • Note: the chemical formula for sucrose (granulated sugar) is C₁₂H₂₂O₁₁. You will find this information very important.

3. 

   Find the temperature of the solution. As we see in the aforementioned Clausius Clapeyron section, the temperature of the liquid will affect its vapor pressure. In general, the higher the temperature, the higher the vapor pressure - as the temperature increases, the more liquid evaporates and increases the pressure in the vessel.
   • In this example, assume the current temperature of the syrup is 298 K (about 25 C).

4. 

   Find the vapor pressure of the solvent. Chemical references typically give vapor pressure values ​​for many common substances and mixtures, but generally only pressure values ​​at 25 ° C / 298 K or at the boiling point temperature. If your solution has this temperature then you can use a reference value, otherwise you need to find the vapor pressure at the initial temperature of the solution.
   • The Clausius-Clapeyron equation can help here, using pressure and temperature 298 K (25 C) for P1 and T1.
   • In this example, the mixture has a temperature of 25 ° C so we can use a lookup table. We see water at 25 ° C with a vapor pressure of 23.8 mmHg

5. 

   Find the molar fraction of the solvent. The last thing you need to do before solving results is to find the molar fraction of the solvent. This is pretty easy: just convert the ingredients to moles, then find the percentage of each of the total moles of the mixture. In other words, the molar portion of each component is equal (number of moles of component) / (total moles of the mixture).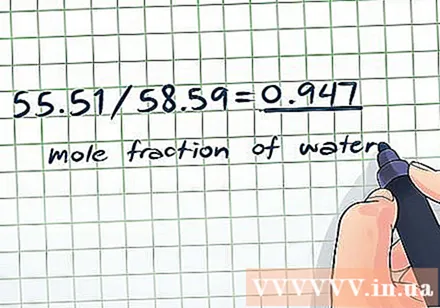
   • Assume that the recipe for the syrup is 1 liter (L) water and 1 liter sucrose (sugar). Then we need to find the number of moles of each ingredient. To do this, we will find the masses of each component, then use the molar mass of those components to work out moles.
   • Weight (1 L water): 1,000 grams (g)
   • Weight (1 L of raw sugar): Approx.1056.7 g
   • Number of moles (water): 1,000 grams × 1 mol / 18,015 g = 55.51 mol
   • Moles (sugar): 1,056.7 grams × 1 mol / 342.2965 g = 3.08 mol (Note that you can find the molar mass of sugar from its chemical formula, C₁₂H₂₂O₁₁.)
   • Total moles: 55.51 + 3.08 = 58.59 moles
   • Molar fraction of water: 55.51 / 58.59 = 0,947

6. 

   Solve results. Finally, we have enough data to solve the Raoult equation. This is very easy: plug the values ​​into variables of the Raoult Theorem equation mentioned at the beginning of this section (P_solution = P_SolventX_Solvent).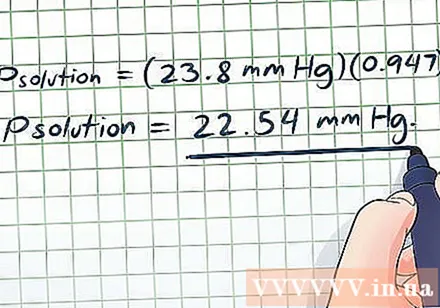
   • Substituting the values, we have:
   • P_solution = (23.8 mmHg) (0.947)
   • P_solution = 22.54 mmHg. This result is reasonable - in molar terms only a little sugar dissolves in a lot of water (although these two are in fact the same volume), so the vapor pressure will only drop a little.
   advertisement

Method 3 of 3: Find steam pressure in special cases

1. 

   Identify Standard Pressure and Temperature conditions. Scientists often use a pair of pressure and temperature values ​​as the "default" conditions. These values ​​are referred to as Standard Pressure and Temperature (collectively referred to as Standard Condition or DKTC). The steam pressure problems often refer to the DKTC, so you should memorize these values ​​for convenience. DKTC is defined as:
   • Temperature: 273.15 K / 0 C / 32 F
   • Pressure: 760 mmHg / 1 atm / 101,325 kilopascals

2. 

   Switch to the Clausius-Clapeyron equation to find other variables. In the example in Part 1, we see that the Clausius-Clapeyron equation is very effective when it comes to calculating the vapor pressure of pure substances. However, not all problems require finding P1 or P2, but many times they even ask to find the temperature or even the ΔH value._vap. In this case, to find the answer, you just need to switch the equation so that the desired variable is on one side of the equation, and all other variables are on the other side.
   • For example, suppose there is an unknown liquid with a vapor pressure of 25 torr at 273 K and 150 torr at 325 K, and we want to find the volatile enthalpy of this liquid (ΔH_vap). We can solve the following:
   • ln (P1 / P2) = (ΔH_vap/ R) ((1 / T2) - (1 / T1))
   • (ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = (ΔH_vap/ R)
   • R × (ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = ΔH_vap. Now let's replace the values:
   • 8,314 J / (K × Mol) × (-1.79) / (- 0.00059) = ΔH_vap
   • 8,314 J / (K × Mol) × 3,033.90 = ΔH_vap = 25,223.83 J / mol

3. 

   Take into account the vapor pressure of the solute as it evaporates. In the above example of Raoult's Law, our solute is sugar so it doesn't evaporate on its own at room temperature (think you've ever seen a bowl of sugar evaporate?). However, when the substance dissolves really If it evaporates, it will affect the general vapor pressure of the solution. We calculate this pressure using the variable equation of Raoult's Law: P_solution = Σ (P_ingredientX_ingredient). The symbol (Σ) means we have to add up all the vapor pressures of the different components to find an answer.
   • For example, let's say we have a solution made up of two chemicals: benzene and toluene. The total volume of the solution is 120 mL; 60 mL of benzene and 60 mL of toluene. The solution temperature is 25 ° C and the vapor pressure of each chemical component at 25 ° C is 95.1 mmHg for benzene, and 28.4 mmHg for toluene. For the given values, find the vapor pressure of the solution. We can solve the problem by using the density, molar mass and vapor pressure of the two chemicals:
   • Volume (benzene): 60 mL = 0.06 L × 876.50 kg / 1,000 L = 0.053 kg = 53 g
   • Weight (toluene): 0.06 L × 866.90 kg / 1,000 L = 0.052 kg = 52 g
   • Number of moles (benzene): 53 g × 1 mol / 78.11 g = 0.679 mol
   • Number of moles (toluene): 52 g × 1 mol / 92.14 g = 0.564 mol
   • Total moles: 0.679 + 0.564 = 1.243
   • Molar fraction (benzene): 0.679 / 1.243 = 0.546
   • Molar fraction (toluene): 0.564 / 1.243 = 0.454
   • Solve results: P_solution = P_benzeneX_benzene + P_toluenX_toluen
   • P_solution = (95.1 mmHg) (0.546) + (28.4 mmHg) (0.454)
   • P_solution = 51.92 mmHg + 12.89 mmHg = 64.81 mmHg
   advertisement

Advice

• To use the Clausius Clapeyron equation above, you must convert the temperature to Kevin units (denoted by K). If you have the temperature in Celsius then change it with the following formula: T_k = 273 + T_c
• You can apply the above methods because energy is proportional to the amount of heat supplied. The temperature of the liquid is the only environmental factor that affects the vapor pressure.