Content

• Steps
• Method 1 of 4: Finding a Set of Function Values ​​Using a Formula
• Method 2 of 4: Finding a Set of Function Values ​​in a Plot
• Method 3 of 4: Finding the Range of a Set of Coordinates
• Method 4 of 4: Finding the Range in Problems
• Tips

The set of values ​​(range of values) of a function is all the values ​​that the function takes in its range of definition. In other words, these are the y values ​​that you get when you substitute all possible x values. All possible values ​​of x and are called the domain of the function. Follow these steps to find the set of values ​​for a function.

Steps

Method 1 of 4: Finding a Set of Function Values ​​Using a Formula

1. 1 Write down the function. For example: f (x) = 3x + 6x -2... By plugging x into the equation, we can find the value of y. This is a quadratic function and its graph is a parabola.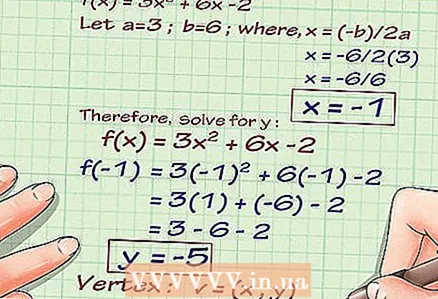
2. 2 Find the vertex of the parabola. If you are given a linear function or any other function with a variable of an odd degree, for example, f (x) = 6x + 2x + 7, skip this step.But if you are given a quadratic function or any other with a variable x in an even power, you need to find the top of the graph of this function. To do this, use the formula x =-b / 2a... In the function 3x + 6x -2 a = 3, b = 6, c = -2. We calculate: x = -6 / (2 * 3) = -1.
   • Now plug x = -1 into the function to find y. f (-1) = 3 * (- 1) + 6 * (- 1) -2 = 3 - 6 -2 = -5.
   • Parabola vertex coordinates (-1, -5). Draw it on the coordinate plane. The point lies in the third quadrant of the coordinate plane.
3. 3 Find a few more points on the graph. To do this, substitute several other values ​​of x into the function. Since the x term is positive, the parabola will point up. As a safety net, we substitute several x values ​​into the function to find out what y values ​​they give.
   • f (-2) = 3 (-2) + 6 (-2) -2 = -2. first point on parabola (-2, -2)
   • f (0) = 3 (0) + 6 (0) -2 = -2. Second point on the parabola (0, -2)
   • f (1) = 3 (1) + 6 (1) -2 = 7. Third point on parabola (1, 7).
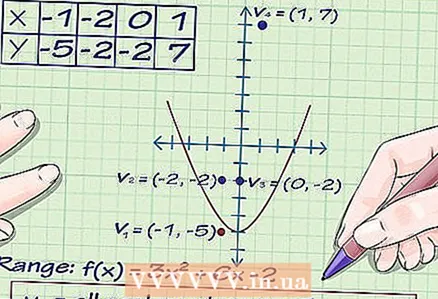4. 4 Find a variety of function values ​​on the graph. Find the smallest y value on the graph. This is the vertex of the parabola, where y = -5. Since the parabola lies above the vertex, the set of values ​​of the function y ≥ -5.

Method 2 of 4: Finding a Set of Function Values ​​in a Plot

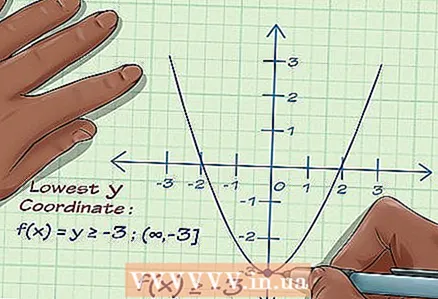1. 1 Find the minimum of the function. Calculate the smallest value for y. Let's say the minimum of the function is y = -3. This value can get smaller and smaller, up to infinity, so that the minimum of the function does not have a given minimum point.
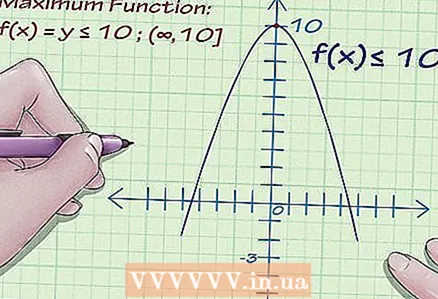2. 2 Find the maximum function. Suppose the maximum of the function y = 10. As in the case of the minimum, the maximum of the function does not have a given maximum point.
3. 3 Write down a variety of meanings. Thus, the range of values ​​of the function is in the range from -3 to +10. Write the set of function values ​​as: -3 ≤ f (x) ≤ 10
   • But, for example, the minimum of the function is y = -3, and its maximum is infinity (the graph of the function goes up infinitely). Then the set of values ​​of the function: f (x) ≥ -3.
   • On the other hand, if the maximum of the function y = 10, and the minimum is infinity (the graph of the function goes down infinitely), then the set of values ​​of the function: f (x) ≤ 10.

Method 3 of 4: Finding the Range of a Set of Coordinates

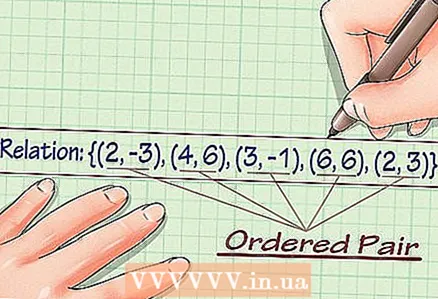1. 1 Write down the set of coordinates. From the set of coordinates, you can determine its range of values ​​and range of definition. Suppose a set of coordinates is given: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.
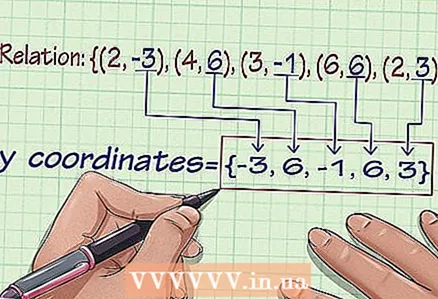2. 2 List the values ​​of y. To find the range of a set, simply write down all the values ​​of y: {-3, 6, -1, 6, 3}.
3. 3 Remove any duplicate values ​​for y. In our example, delete "6": {-3, -1, 6, 3}.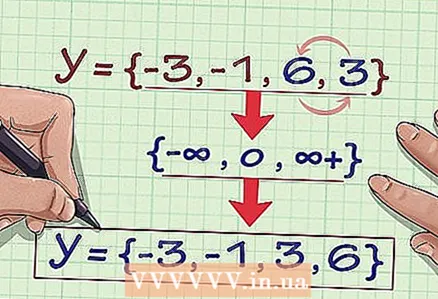
4. 4 Write down the range in ascending order. The range of values ​​of the set of coordinates {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} will be {-3, -1, 3, 6}.
5. 5 Make sure a set of coordinates is given for the function. For this to be the case, for every single x-value there must be one y-value. For example, the set of coordinates {(2, 3) (2, 4) (6, 9)} is not given for a function, because one value x = 2 corresponds to two different values ​​of y: y = 3 and y = 4.

Method 4 of 4: Finding the Range in Problems

1. 1 Read the problem. “Olga sells theater tickets for 500 rubles per ticket. The total proceeds for tickets sold is a function of the number of tickets sold. What is the range of this function? "
2. 2 Write the task as a function. In this case M is the total proceeds for tickets sold, and t - the number of tickets sold. Since one ticket costs 500 rubles, you need to multiply the number of tickets sold by 500 to find the proceeds. Thus, the function can be written as M (t) = 500t.
   • For example, if she sells 2 tickets, you need to multiply 2 by 500 - as a result, we get 1000 rubles for the tickets sold.
3. 3 Find the scope. To find the range, you must first find the range. These are all possible values ​​of t. In our example, Olga can sell 0 or more tickets - she cannot sell a negative number of tickets. Since we do not know the number of seats in the theater, it can be assumed that, in theory, she could sell an infinite number of tickets. And she can only sell whole tickets (she cannot sell 1/2 a ticket, for example). Thus, the domain of the function t = any non-negative integer.
4. 4 Find the range. This is the possible amount of money that Olga will help out from ticket sales.If you know that the domain of a function is any non-negative integer, and the function is: M (t) = 5t, then you can find the proceeds by substituting any non-negative integer into the function (instead of t). For example, if she sells 5 tickets, then M (5) = 5 * 500 = 2500 rubles. If she sells 100 tickets, then M (100) = 500 x 100 = 50,000 rubles. Thus, the range of values ​​of the function is any non-negative integers divisible by five hundred.
   • This means that any non-negative integer that is divisible by 500 is the value of y (the proceeds) of our function.

Tips

• In more complex cases, it is better to first draw a graph using the range of definition, and only then find the range.
• See if you can find the inverse function. The domain of the inverse function is equal to the domain of the original function.
• Check if the function is repeatable. Any function that repeats along the x-axis will have the same range for the entire function. For example, the range for f (x) = sin (x) will be -1 to 1.