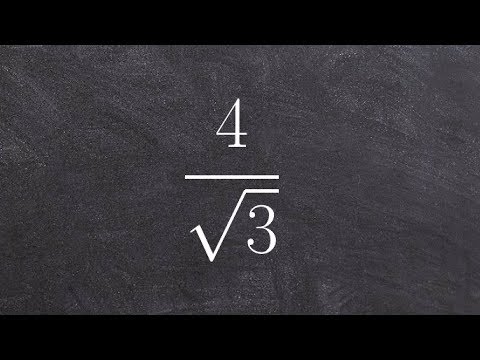
Content

• Steps
• Method 1 of 4: Monomial in the denominator
• Method 2 of 4: Binomial in the denominator
• Method 3 of 4: Reverse Expression
• Method 4 of 4: Cubic Root in the Denominator

In mathematics, it is not customary to leave a root or an irrational number in the denominator of a fraction. If the denominator is a root, multiply the fraction by some term or expression to get rid of the root. Modern calculators allow you to work with roots in the denominator, but the educational program requires that students be able to get rid of the irrationality in the denominator.

Steps

Method 1 of 4: Monomial in the denominator

1. 1 Learn the fraction. The fraction is written correctly if there is no root in the denominator. If the denominator has a square or any other root, you need to multiply the numerator and denominator by some monomial to get rid of the root. Please note that the numerator can contain a root - this is normal.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}}}$
   • The denominator here has a root ${ displaystyle { sqrt {7}}}$.
2. 2 Multiply the numerator and denominator by the root of the denominator. If the denominator contains a monomial, it is quite easy to rationalize such a fraction. Multiply the numerator and denominator by the same monomial (that is, you are multiplying the fraction by 1).
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}}}$
   • If you are entering an expression for a solution on a calculator, be sure to put parentheses around each part to separate them.
3. 3 Simplify the fraction (if possible). In our example, it can be abbreviated by dividing the numerator and denominator by 7.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}} = { frac {7 { sqrt {21}}} {14}} = { frac { sqrt {21}} {2}}}$

Method 2 of 4: Binomial in the denominator

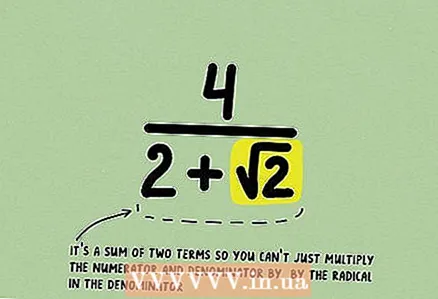1. 1 Learn the fraction. If its denominator contains the sum or difference of two monomials, one of which contains a root, you cannot multiply the fraction by such a binomial to get rid of irrationality.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}}}$
   • To understand this, write down the fraction ${ displaystyle { frac {1} {a + b}}}$where the monomial ${ displaystyle a}$ or ${ displaystyle b}$ contains the root. In this case: ${ displaystyle (a + b) (a + b) = a ^ {2} + 2ab + b ^ {2}}$... Thus, the monomial ${ displaystyle 2ab}$ will still include the root (if ${ displaystyle a}$ or ${ displaystyle b}$ contains the root).
   • Let's take a look at our example.
     • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 + { sqrt {2}}} {2 + { sqrt {2}}}} = { frac {4 (2 + { sqrt {2}})} {4 + 4 { sqrt {2}} + 2}}}$
   • You see that you cannot get rid of the monomial in the denominator ${ displaystyle 4 { sqrt {2}}}$.
2. 2 Multiply the numerator and denominator by the binomial conjugate of the binomial in the denominator. A conjugate binomial is a binomial with the same monomial, but with the opposite sign between them. For example, binom ${ displaystyle 2 + { sqrt {2}}}$ conjugated to a binomial ${ displaystyle 2 - { sqrt {2}}.}$
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}}}$
   • Understand the meaning of this method. Consider the fraction again ${ displaystyle { frac {1} {a + b}}}$... Multiply the numerator and denominator by the binomial conjugate to the binomial in the denominator: ${ displaystyle (a + b) (a-b) = a ^ {2} -b ^ {2}}$... Thus, there are no monomials that contain roots. Since the monomials ${ displaystyle a}$ and ${ displaystyle b}$ are squared, the roots will be eliminated.
3. 3 Simplify the fraction (if possible). If there is a common factor in both the numerator and denominator, cancel it. In our case, 4 - 2 = 2, which can be used to reduce the fraction.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}} = { frac {4 (2 - { sqrt {2}})} {4-2}} = 4-2 { sqrt {2}}}$

Method 3 of 4: Reverse Expression

1. 1 Examine the problem. If you need to find an expression that is the inverse of the given one, which contains a root, you will have to rationalize the resulting fraction (and only then simplify it). In this case, use the method described in the first or second sections (depending on the task).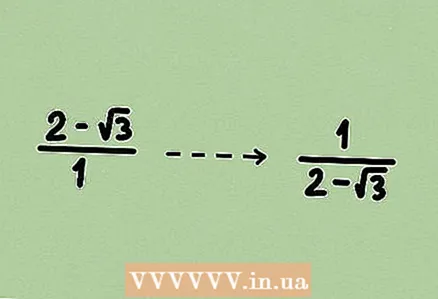
   • ${ displaystyle 2 - { sqrt {3}}}$
2. 2 Write down the opposite expression. To do this, divide 1 by the given expression; if given a fraction, swap the numerator and denominator. Remember that any expression is a fraction with 1 in the denominator.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}}}$
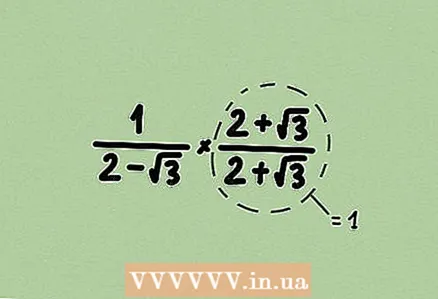3. 3 Multiply the numerator and denominator by some expression to get rid of the root. By multiplying the numerator and denominator by the same expression, you are multiplying the fraction by 1, that is, the value of the fraction does not change. In our example, we are given a binomial, so multiply the numerator and denominator by the conjugate binomial.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}}}$
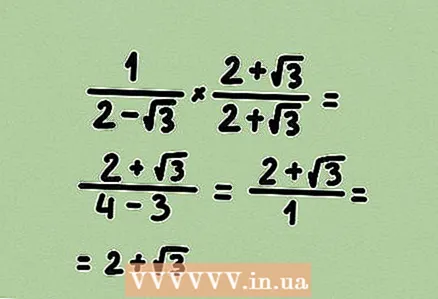4. 4 Simplify the fraction (if possible). In our example, 4 - 3 = 1, so the expression in the denominator of the fraction can be canceled completely.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}} = { frac {2 + { sqrt {3}}} {4-3}} = 2 + { sqrt {3}}}$
   • The answer is a binomial conjugate to this binomial. It's just a coincidence.

Method 4 of 4: Cubic Root in the Denominator

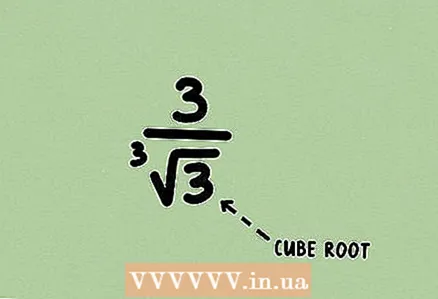1. 1 Learn the fraction. The problem may contain cube roots, although this is quite rare. The described method is applicable to roots of any degree.
   • ${ displaystyle { frac {3} { sqrt [{3}] {3}}}}$
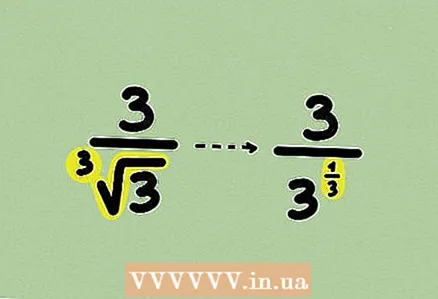2. 2 Rewrite the root as a power. Here you cannot multiply the numerator and denominator by some monomial or expression, because rationalization is carried out in a slightly different way.
   • ${ displaystyle { frac {3} {3 ^ {1/3}}}}$
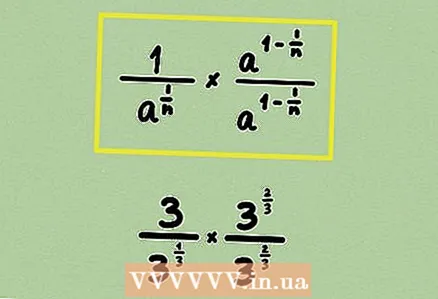3. 3 Multiply the numerator and denominator of the fraction by some power so that the exponent in the denominator becomes 1. In our example, multiply the fraction by ${ displaystyle { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$... Remember that when the degrees are multiplied, their indicators add up: ${ displaystyle a ^ {b} a ^ {c} = a ^ {b + c}.}$
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$
   • This method is applicable to any roots of degree n. If a fraction is given ${ displaystyle { frac {1} {a ^ {1 / n}}}}$, multiply the numerator and denominator by ${ displaystyle a ^ {1 - { frac {1} {n}}}}$... Thus, the exponent in the denominator becomes 1.
4. 4 Simplify the fraction (if possible).
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}} = 3 ^ {2/3 }}$
   • If necessary, write down the root in the answer. In our example, factor the exponent into two factors: ${ displaystyle 1/3}$ and ${ displaystyle 2}$.
     • ${ displaystyle 3 ^ {2/3} = (3 ^ {2}) ^ {1/3} = { sqrt [{3}] {9}}}$