Content

• Steps
• Advice

Velocity is defined as the speed of an object in a given direction. In many cases, to find velocity we will use the equation v = s / t, where v is the velocity, s is the total distance of the object's displacement from its original position, and t is the time it takes for the object to travel. go all the way. However, in theory this formula is only for velocity medium of things on the way. By calculating the velocity of the object at any point along the distance. That is Transportation time and is defined by the equation v = (ds) / (dt), or in other words, it is the derivative of the equation for the average velocity.

Steps

Part 1 of 3: Calculate instantaneous velocity

1. 

   
   
   Start with an equation for calculating velocity by displacement distance. To find the instantaneous velocity, we must first have an equation that indicates the position of the object (in terms of displacement) at any given moment. That means the equation must have only one variable S on one side and turn t On the other side (not necessarily only one variable), like this:
   

   s = -1.5t + 10t + 4

   • In this equation, the variables are:

     s = displacement. The distance the object moved from its original position. For example, if an object can walk 10 meters forward and 7 meters backward, its total travel distance is 10 - 7 = 3 meters (not 10 + 7 = 17m).

     t = time. This variable is simple without explanation, usually measured in seconds.

2. 

   
   
   Take the derivative of the equation. The derivative of the equation is another equation that shows the slope of the distance at a particular time. To find the derivative of the equation by displacement distance, take the differential of the function according to the following general rule to calculate the derivative: If y = a * x, Derivative = a * n * x. This applies to all terms on the "t" side of the equation.
   • In other words, begin to get the differential left to right on the "t" side of the equation. Whenever you encounter the variable "t", you subtract the exponent by 1 and multiply the term by the original exponent. Any constant terms (terms without "t") will disappear because they are multiplied by 0. The process isn't as hard as you might think - let's take the equation in the above step as an example:
     

     s = -1.5t + 10t + 4
     (2) -1.5t + (1) 10t + (0) 4t
     -3t + 10t
     -3t + 10

     
     

3. 

   Replace "s" with "ds / dt". To show that the new equation is the derivative of the original square, we replace "s" with the symbol "ds / dt". In theory, this notation is "the derivative of s in terms of t". A simpler way to understand this notation, ds / dt is the slope of any point in the initial equation. For example, to find the slope of the distance described by the equation s = -1.5t + 10t + 4 at time t = 5, we substitute "5" for t in the derivative of the equation.
   • In the above example, the derivative of the equation looks like this:
     

     ds / dt = -3t + 10

4. 

   Substitute a value for t into the new equation to find the instantaneous velocity. Now that we have the derivative equation, finding the instantaneous velocity at any given moment is very easy. All you need to do is choose a t-value and replace it with the derivative equation. For example, if we want to find the instantaneous velocity at t = 5, we just need to substitute "5" for t in the derivative equation ds / dt = -3t + 10. We will solve the equation like this:
   

   ds / dt = -3t + 10
   ds / dt = -3 (5) + 10
   ds / dt = -15 + 10 = -5 meters / second

   • Note that we use the unit "meters / second" above.Since we are solving the problem with displacement in meters and time in seconds, and speed is the displacement in time, this unit is suitable.
   advertisement

Part 2 of 3: Estimating instantaneous velocity graphically

1. 

   Graph the object's movement distance over time. In the above section, we said that the derivative is also a formula that allows us to find the slope at any point in the equation taken from the derivative. In fact, if you show the moving distance of the object on a graph, The slope of the graph at any point is the instantaneous velocity of the object at that point.
   • To graph motion distances, use the x-axis for time and the y-axis for displacement. You then determine a number of points by plugging the values ​​of t into the motion equation, the result is s values, and you dot the points t, s (x, y) on the graph.
   • Note that the graph may extend below the x-axis. If the line showing the movement of the object goes down the x-axis, this means that the object moves backwards from its original position. In general, the graph won't extend behind the y-axis - we usually don't measure the velocity of objects moving back in time!

2. 

   Select a point P and a point Q located near point P on the graph. To find the slope of the graph at point P, we use the technique of "limit finding". Finding a limit means taking two points (P and Q (a point near P)) on the curve and finding the slope of the line connecting those two points, repeating this process as the distance between P and Q shortens. gradually.
   • Suppose the displacement distance has points (1; 3) and (4; 7). In this case, if we want to find the slope at (1; 3) then we can set (1; 3) = P and (4; 7) = Q.

3. 

   Find the slope between P and Q. The slope between P and Q is the difference of the y values ​​for P and Q over the difference of the x values ​​for P and Q. In other words, H = (y_Q - y_P) / (x_Q - x_P), where H is the slope between two points. In this example, the slope between P and Q is:
   

   H = (y_Q - y_P) / (x_Q - x_P)
   H = (7 - 3) / (4 - 1)
   H = (4) / (3) = 1,33

4. 

   Repeat several times by moving Q closer to P. The goal is to narrow the distance between P and Q until they reach a single point. The smaller the distance between P and Q, the closer the slope of that infinitely small segment will be to the slope at point P. Repeat a few times for our example equation, using points (2; 4 , 8), (1.5; 3.95) and (1.25; 3.49) give Q and the initial coordinates of P are (1; 3):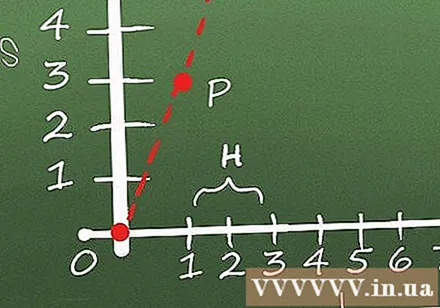
   

   Q = (2; 4.8): H = (4.8 - 3) / (2 - 1)
   H = (1.8) / (1) = 1,8
   
   Q = (1.5; 3.95): H = (3.95 - 3) / (1.5 - 1)
   H = (0.95) / (0.5) = 1,9
   
   Q = (1.25; 3.49): H = (3.49 - 3) / (1.25 - 1)
   H = (0.49) / (0.25) = 1,96

5. 

   Estimates the slope of the extremely small segment on the graph curve. As Q gets closer and closer to P, H will gradually get closer to the slope at P. Finally, at a very small line, H will be the slope at P. Because we cannot measure or calculate The length of a line is extremely small, so only estimate the slope at P when it is clearly visible from the points we compute.
   • In the above example, as we move H closer to P, we have the values ​​for H of 1,8; 1.9 and 1.96. Since these numbers are getting closer to 2 we can say 2 is the approximate value of the slope at P.
   • Remember that the slope at any point on the graph is the derivative of the graph equation at that point. Since the graph shows an object's displacement over time, as we saw in the previous section, its instantaneous velocity at any point is the derivative of the object's displacement distance at the problem point. Access, we can say 2 meters per second is an approximate estimate of the instantaneous velocity when t = 1.
   advertisement

Part 3 of 3: Sample problem

1. 

   Find the instantaneous velocity when t = 1 with the displacement equation s = 5t - 3t + 2t + 9. Like the example in the first section, but this is a cubic instead of quadratic, so we can solve the problem in the same way.
   • First, take the derivative of the equation:
     

     s = 5t - 3t + 2t + 9
     s = (3) 5t - (2) 3t + (1) 2t
     15t - 6t + 2t - 6t + 2

   • Then we replace the value of t (4) in:
     

     s = 15t - 6t + 2
     15(4) - 6(4) + 2
     15(16) - 6(4) + 2
     240 - 24 + 2 = 22 meters per second

2. 

   Use the graph estimation method to find the instantaneous velocity at (1; 3) for the displacement equation s = 4t - t. For this problem, we use coordinates (1; 3) as point P, but must find other Q points located near it. Then all we need to do is find the H values ​​and deduce the estimated value.
   • First, we find Q points when t = 2; 1.5; 1.1 and 1.01.
     

     s = 4t - t
     
     t = 2: s = 4 (2) - (2)
     4 (4) - 2 = 16 - 2 = 14, so Q = (2; 14)
     
     t = 1.5: s = 4 (1.5) - (1.5)
     4 (2.25) - 1.5 = 9 - 1.5 = 7.5, so Q = (1.5; 7.5)
     
     t = 1.1: s = 4 (1.1) - (1.1)
     4 (1.21) - 1.1 = 4.84 - 1.1 = 3.74, so Q = (1.1; 3.74)
     
     t = 1.01: s = 4 (1.01) - (1.01)
     4 (1,0201) - 1.01 = 4.0804 - 1.01 = 3.0704, so that's it Q = (1.01; 3.0704)

   • Next we will get H values:
     

     Q = (2; 14): H = (14 - 3) / (2 - 1)
     H = (11) / (1) = 11
     
     Q = (1.5; 7.5): H = (7.5 - 3) / (1.5 - 1)
     H = (4,5) / (0.5) = 9
     
     Q = (1.1; 3.74): H = (3.74 - 3) / (1.1 - 1)
     H = (0.74) / (0.1) = 7,3
     
     Q = (1.01; 3.0704): H = (3.0704 - 3) / (1.01 - 1)
     H = (0.0704) / (0.01) = 7,04

   • Since H values ​​seem to be closer to 7, we can say that 7 meters per second is the approximate estimate of the instantaneous velocity at the coordinate (1; 3).
   advertisement

Advice

• To find acceleration (change in velocity over time), use the method in part one to get the derivative of the displacement equation. Then take the derivative again for the derivative equation you just found. As a result, you have an equation for the acceleration at a given point in time - all you have to do is plug in the time.
• The equation showing the relationship between Y (displacement distance) and X (time) can be very simple, like Y = 6x + 3. In this case, the slope is constant and it is not necessary to take the derivative to calculate the slope, that is, it follows the basic equation form Y = mx + b for a linear graph, ie the slope equals 6.
• The displacement distance is the same as distance but has a direction, so it is a vector quantity, and speed is a scalar quantity. Travel distances may be negative, while distances may only be positive.