Content

• Steps

One of the most common problems in geometry is calculating the area of ​​a circle based on known information. The formula for the area of ​​a circle is:. The formula is quite simple, you just need to know the value of the radius to get the area of ​​the circle. However, you also need to practice converting some of the given data units into terms that are applicable to this formula.

Steps

Method 1 of 4: Use radius to find area

1. 

   Determine the radius of the circle. The radius is the length from the center to the edge of the circle. Either way, the radius is the same. The radius is also half the diameter of a circle. The diameter is the line that crosses the center and connects the opposite sides of the circle together.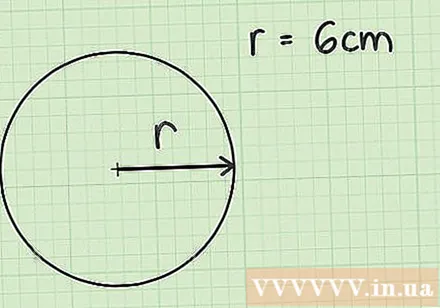
   • The subject is usually given a radius. It is quite difficult to determine the exact center of the circle unless it is already indicated on the drawing in the project.
   • In this example, suppose the problem gives you a radius of a circle of 6 cm.

2. 

   
   
   Square of radius. The formula for the area of ​​a circle is, where the variable represents the radius. This variable is squared up.
   • Don't confuse and square the entire expression.
   • Example: a circle has radius, we have.

3. 

   
   
   Multiply by pi. Pi is a mathematical constant that represents the ratio between the circumference and the diameter of a circle. It is symbolized by the Greek letter. After rounding to decimals, it is almost 3.14. True decimal values ​​are actually infinitely long. Normally, to represent the area of ​​a circle correctly, we would write the answer symbolically.
   • For the example of a circle with a radius of 6 cm, the area would be calculated as follows:
     • good

4. 

   
   
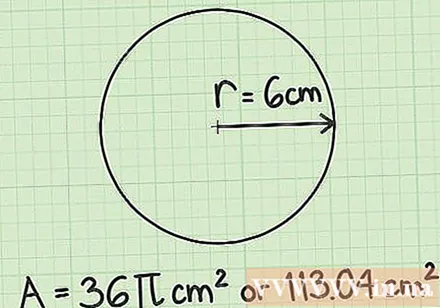
   Present your answer. Remember that when calculating area, the unit must always be displayed with the sign "squared" (pronounced square). If the radius was in centimeters, the area would be centimeters. If the radius was measured in meters, the area would be square meters. You also need to know how to ask us to represent the answer: notation or work out a rounded decimal? If you don't know, go through both ways.
   • For a circle with a radius of 6 cm, the area would be 36 cm or 113.04 cm.
   advertisement

Method 2 of 4: Calculate the area by diameter

1. 

   Measure or rewrite the diameter. In some problems or situations, you will not know the radius. Instead, you will only know the diameter length of the circle. If the diameter is plotted in the problem diagram, you can use a ruler to measure it. Or, the problem will be given the length of the diameter.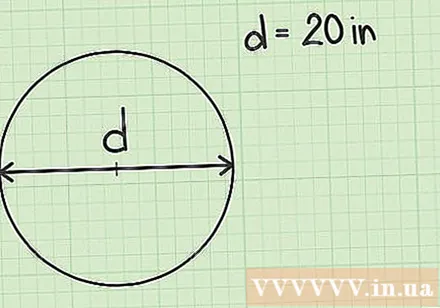
   • Suppose, you have a circle with a diameter of 20 cm.

2. 

   Split the diameter. Remember that the diameter is twice as long as the radius. So no matter what the diameter of the problem is, just divide it in half and you get the radius.
   • In the above example, a circle with a diameter of 20 cm will have a radius of 20/2 = 10 cm.

3. 

   Use the basic area stick formula. After converting the diameter to a radius, it's time to use the formula to calculate the area of ​​a circle. Assign the value of the radius and perform the remaining calculation as follows:

4. 

   Describe the value of the area. Again, the circle's area unit will go with the sign "squared". In this example, the diameter is in cm, so the radius is also in cm. So, the area will be calculated in square centimeters. The answer here will be cm.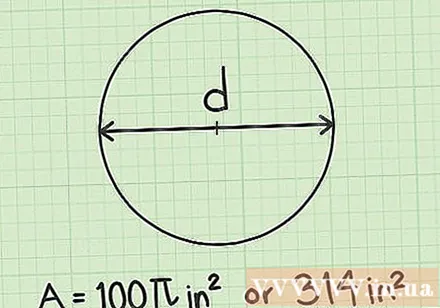
   • You can also supply a decimal by substituting 3.14 for. The result of the equation is (100) (3.14) = 314 cm.
   advertisement

Method 3 of 4: Use perimeter to calculate area

1. 

   Learn about transformation formulas. If you know the circumference of the circle, you can use the transform formula to find the area of ​​the circle. This transformation formula directly assigns the perimeter value to calculate the area, you don't need to find the radius. The new formula is: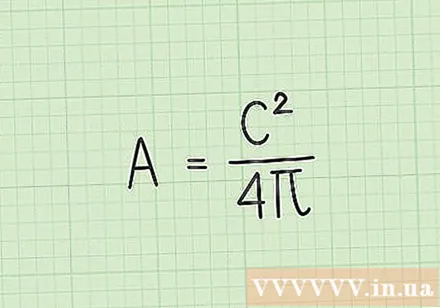

2. 

   Measure or write down the circumference. In some real world situations, you may not be able to measure the diameter or the radius accurately. It is difficult to estimate the center of the circle if the diameter or center of the circle is not specified. For some circular objects - such as a pizza pan or a frying pan - you can use a tape measure to measure the circumference, much more accurately than measuring the diameter.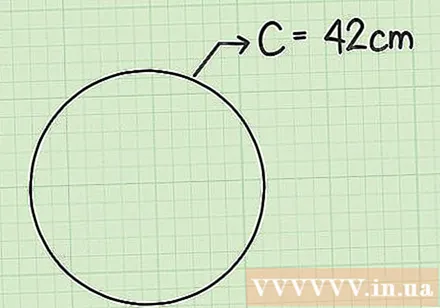
   • In this example, suppose you have a circle (or a circular object) with a circumference of 42 cm.

3. 

   Use the relationship between perimeter and radius to transform the formula. The circumference of a circle is equal to pi multiplied by the diameter or. Next, recall that the diameter is twice the radius, or. You can combine these two expressions to create the following relationship:. Rearranging the expression to isolate the variable r, we have:
   • ... .. (divided by 2 sides)

4. 

   Replace the formula for the area of ​​a circle. Using the relationship between perimeter and radius, you can create a modified version of the circle area formula. Putting the last expression in the formula for the original area, we have:
   • ... .. (formula to calculate the initial area)
   • ... .. (replace the expression of r in)
   • ... .. (square fraction)
   • ... .. (simple in the numerator and denominator)

5. 

   
   
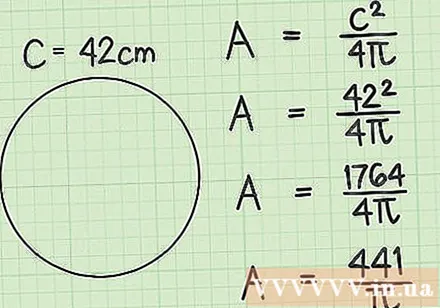
   Apply the transform formula to calculate the area. Apply the rewritten transformation formula with perimeter instead of radius along with the information you have to find the exact area. Assign the value of perimeter and perform the calculation as follows:
   • In this example, you have a perimeter of centimeters.
   • ... .. (insert value)
   • .…. (Count 42)
   • ... .. (divided by 4)

6. 

   
   
   Give the answer. Unless the perimeter you have is a multiple of, your result will be a fraction with the denominator. This answer is not wrong. You should either present your area answer this way, or you should work out your approximate answer by replacing pi with 3.14.
   • In this example, a circle with a circumference of 42 cm will have an area of ​​cm
   • If we want to calculate decimals, we have. The area is nearly 140 cm.
   advertisement

Method 4 of 4: Calculate the area with a fan

1. 

   
   
   
   
   Identify information known or given. Some problems will give you information about the fan shape of the circle and the problem will ask you to calculate the total area of ​​the circle. Read the text carefully and look for information similar to, “A fan of an O circle has an area of ​​15 cm. Calculate the area of ​​a circle O. ”

2. 

   
   
   Determine the fan shape given. The fan shape of the circle is part of the circle. A fan shape is defined by drawing two lines with radius from the center to the edge of the circle. The space between the two radii is the fan shape.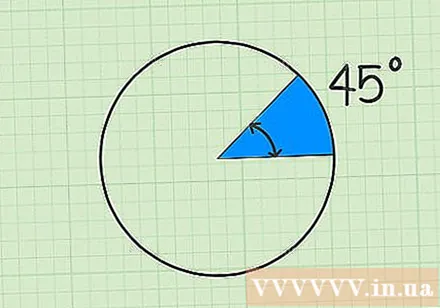

3. 

   
   
   Calculate the angle at the center of the fan shape. Use a protractor to measure the angle between the two radii. Place the bottom edge of the protractor along a radius, the center of the ruler coincident with the center of the circle. Then read the angle measurement located at the second radius forming a fan.
   • Make sure you measure the small angle between the two radii and not the larger outside angle. Usually, the problem you're solving will give you this figure. The sum of the small and big angles will be 360 ​​degrees.
   • In some problems, the problem will give you the measure of the angle. Example: “The angle at the center of the fan shape is 45 degrees”, if there are no data available, you will have to take a measurement.

4. 

   Apply the transformation formula to calculate the area. Once you know the area of ​​the fan shape and the measure of the angle at its center, you can apply the transform formula to find the area of ​​the circle: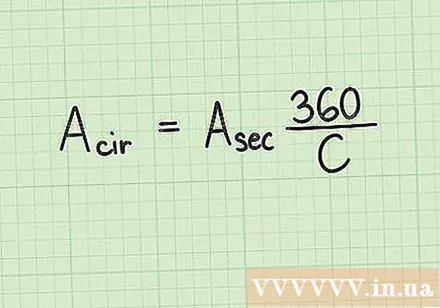
   • • is the total area of ​​the circle
     • is the area of ​​the fan shape
     • is the measure of the angle at the center

5. 

   Enter the values ​​you know and calculate the area. In this example, you should have a center angle of 45 degrees and a fan shape of 15. Replace these numbers in the formula and proceed as follows:

6. 

   Give the answer. In this example, the fan shape equals 1/8 of the total area of ​​the circle. So, the total area of ​​the circle is 120 cm. The original fan-shaped area is given, so you should present the area of ​​the entire circle in a similar way.
   • If you want to present your answers numerically, do the calculation 120 x 3.14 and the result is 376.8 cm.
   advertisement