Content

• Steps
• Advice

The arc is any segment on the circumference of the circle. The arc length is the distance from one end of the arc to the other. To find arc lengths, you need some knowledge of circle geometry. Since the arc is part of the perimeter, if you know how many degrees the angle at the center of the arc is, it is easy to find the length of that arc.

Steps

Method 1 of 2: Use a central angle measurement in degrees

1. 

   Set up the formula for the length of the arc. The formula is, where is the radius of the circle and is the measure of the angle at the center of the arc.

2. 

   
   
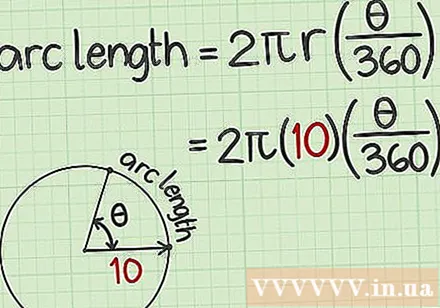
   Plug the radius length into the formula. This information must be given the subject, or you can measure it. Remember to put this value in the variable.
   • For example, if the circle's radius is 10cm, the formula will look like this:.

3. 

   Replace the angle measure at the center of the arc into the formula. This information must be given the subject, or you can measure it. You must use degrees, not radians, when using this formula. Replace the central angle measurement into the formula.
   • For example, if the angular measure at the center of the arc was 135 degrees, the formula would look like this:.

4. 

   
   
   Multiply the radius by. If you are not using a calculator, approximate values ​​can be used for calculations. Rewrite the formula with this new value to represent the circumference of the circle.
   • For example:
     
     
     

5. 

   Divide the center angle of the arc by 360. Since the circle has 360 degrees, this calculation will tell you how many parts the arc occupies on the whole circle. With this information, you can find out how many parts per circumference the arc length is.
   • For example:
     
     

6. 

   
   
   Multiply two numbers together. You will find the arc length value.
   • For example:
     
     
     So the arc length of a circle with a radius of 10cm, with an angle at the center of 135 degrees, is about 23.55 cm.
   advertisement

Method 2 of 2: Use the center angle measure in radians

1. 

   Set up the formula for the length of the arc. The formula is, where is the measure of the angle at the center of the arc in radians, and is the length of the radius of the circle.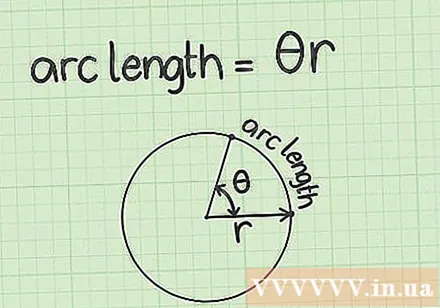

2. 

   Plug the radius length into the formula. You need to know the radius length to be able to use this method. Remember to add the radius length to the variable.
   • For example, if the circle's radius is 10cm, the formula would look like this:.

3. 

   Replace the angle measure at the center of the arc into the formula. You must be supplied with this value in radians. If you know the angle measurements in degrees it is not possible to use this method.
   • For example, if the angular measure at the center of the arc was 2.36 radians, the formula would look like this:.

4. 

   Multiply the radius by the radian measurement. You will find the arc length value.
   • For example:
     
     
     So, the arc length of a circle with a radius of 10cm, with a central angle of 23.6 radians, is about 23.6 cm.
   advertisement

Advice

• If you know the diameter of the circle, you can still find the arc length. In the arc length formula, there is a radius of the circle. Since the radius is half the diameter, to find the radius, you just need to divide the diameter by 2. For example, if the diameter of the circle is 14 cm, you would divide 14 by 2 to get the radius:
  .
  Therefore, the radius of the circle is 7 cm.