Content

• Steps
• Advice

If you are a mathematician or a graphic programmer, you will probably have to find the angle between two given vectors. In this article, wikiHow shows you how to do just that.

Steps

Part 1 of 2: Find the angle between two vectors

1. 

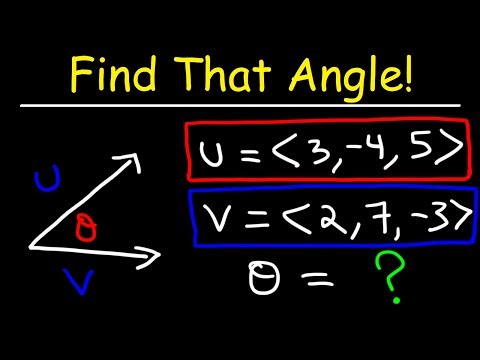
   Vector definition. Write down all the information about the two vectors you have. Suppose you only have the specified parameters of their dimensional coordinates (also called components). If you already know the length (magnitude) of a vector, you can skip some of the steps below.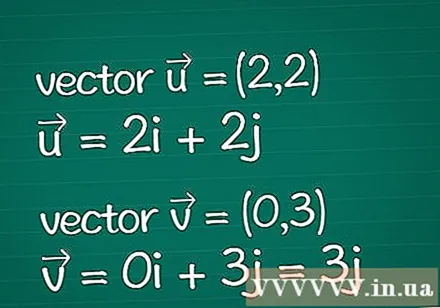
   • Example: Two-dimensional vector = (2,2) and two-dimensional vector = (0,3). They can also be written as = 2i + 2j and = 0i + 3j = 3j.
   • Although two-dimensional vectors are used in the example in this article, the following instructions can apply to vectors with any number of dimensions.

2. 

   
   
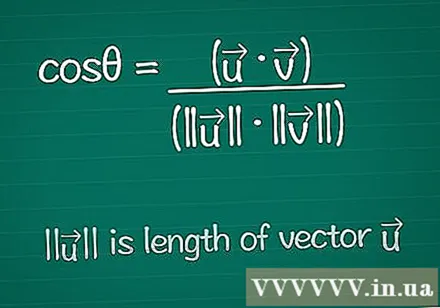
   Write down the cosine formula. To find the angle θ between two vectors, we start with the formula for finding the cosine for that angle. You can learn about this formula below, or just write it down like this:
   • cosθ = (•) / (|||| ||||)
   • |||| means "length of the vector".
   • • is the scalar product of the two vectors - this will be explained below.

3. 

   
   
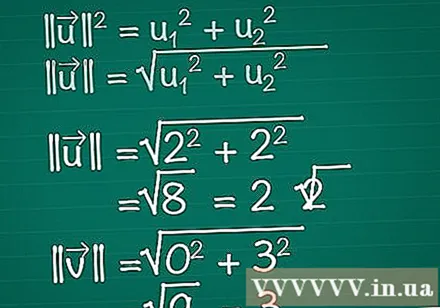
   Calculate the length of each vector. Imagine a right triangle is made up of the x, y components of the vector, and the vector itself. The vector forms the hypotenuse of the triangle, so to find its length we use the Pythagorean theorem. In fact, this formula can be easily extended to a vector of any number of dimensions.
   • || u || = u₁ + u₂. If a vector has more than two elements, you just need to keep adding + u₃ + u₄ +...
   • Hence, for a two-dimensional vector, || u || = √ (u₁ + u₂).
   • In this example, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
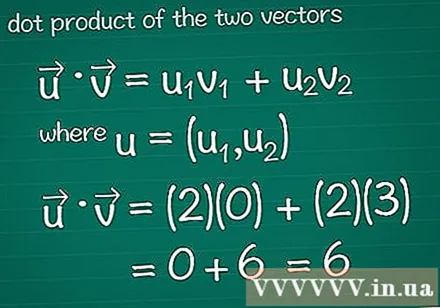
   Calculate the scalar product of two vectors. Perhaps you've learned the method of vector multiplication, also known as scalar this. To calculate the scalar product relative to their composition, multiply the ingredients in each direction together, then add up the entire result.
   • For the graphics program, please refer to Tips before reading further.
   • In math • = u₁v₁ + u₂v₂, where, u = (u₁, u₂). If the vector has more than two elements, simply add + u₃v₃ + u₄v₄...
   • In this example, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. This is the scalar product of the vector and the vector.

5. 

   Put the results in the formula. Remember that cosθ = (•) / (|||| || ||). Now we know both the scalar product and the length of each vector. Enter these into the formula to calculate the cosine of the angle.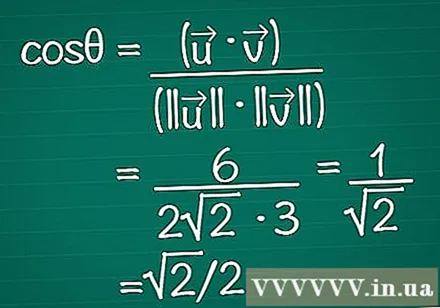
   • In our example, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Find the angle based on its cosine. You can use the arccos or cos function in a calculator to find θ from a known cos value. With some results, you may find the angle based on the unit circle.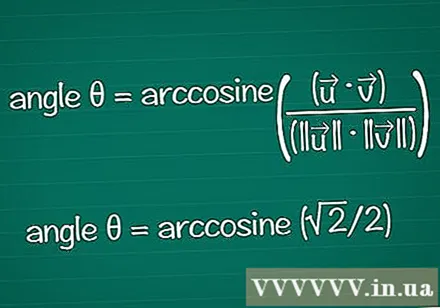
   • In the example, cosθ = √2 / 2. Enter "arccos (√2 ​​/ 2)" in your calculator to find the angle. Or, you can find angle θ on the unit circle, at position cosθ = √2 / 2. It is true for θ = /₄ or 45º.
   • Combining everything, the final formula is: angle θ = arccosine ((•) / (|||| || ||))
   advertisement

Part 2 of 2: Determination of angle formula

1. 

   Understand the purpose of the formula. This formula was not derived from existing rules. Instead, it is formed as the definition of the scalar product and the angle between the two vectors. Even so, it was not an arbitrary decision. Going back to basic geometry, we can understand why this formula provides intuitive and useful definitions.
   • The examples below use two-dimensional vectors because they are easiest to understand and simplest. Three-dimensional or more vectors have properties defined by almost similar general formulas.

2. 

   Review Cosine's theorem. Consider an ordinary triangle with angle θ between sides a and b, opposite side c. The Cosine Theorem states that c = a + b -2abcos(θ). This result is drawn quite simply from basic geometry.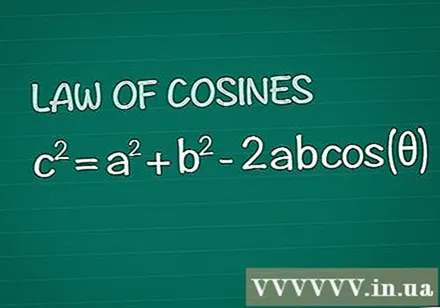

3. 

   Connect two vectors, forming a triangle. Draw a pair of two-dimensional vectors on paper, vectors and vectors, with θ being the angle between them. Draw a third vector between these two to create a triangle. In other words, draw a vector such that + =. Vector = -.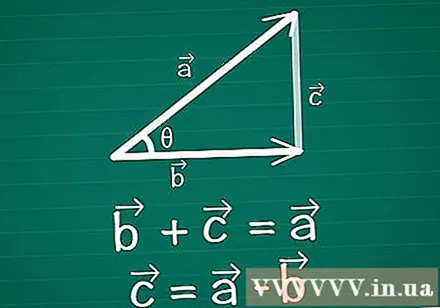

4. 

   Write the Cosine theorem for this triangle. Substitute the side length of our "vector triangle" into the Cosine theorem:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Rewrite with scalar product. Remember, a scalar product is the image of one vector on the other. The scalar product of a vector with itself requires no projection, because here, there is no difference in direction. That means • = || a ||. Using this, we rewrite the equation:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Successfully rewrote the same formula. Expand the left side of the formula, then simplify to get the formula used to find angles.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   advertisement

Advice

• To change values ​​and solve the problem quickly, use this formula for any pair of two-dimensional vectors: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• If you're working with computer graphics software, chances are you will only have to care about the vectors dimension without worrying about their length. Use the following steps to shorten an equation and speed up your program:
  • Normalize each vector so that they are equal to 1. To do this, divide each of the vector's components by its length.
  • Get the normalized product of the scalar instead of the original vector.
  • Since the length is 1, we can exclude the length elements from the equation. Finally, the angle equation obtained is arccos (•).
• Based on the cosine formula, we can quickly determine whether the angle is acute or obtuse. Start with cosθ = (•) / (|||| ||||):
  • The left and right sides of the equation must have the same sign (positive or negative).
  • Since length is always positive, cosθ must have the same sign as the scalar product.
  • Therefore, if the product is a positive, cosθ is also positive. We are in the first quadrant of the unit circle, with θ <π / 2 or 90º. The angle to find is the sharp angle.
  • If the scalar product is negative, cosθ is negative. We are in the second quadrant of the unit circle, with π / 2 <θ ≤ π or 90º <θ ≤ 180º. That is the prison corner.