Formulating mathematical proofs

Video: Four Basic Proof Techniques Used in Mathematics

Content

To step
Method 1 of 3: Understanding the problem
Method 2 of 3: Structuring a proof
Method 3 of 3: Formulating the evidence
Tips

Mathematical proofs can be difficult, but with the right background knowledge of both math and the structure of a proof, you can certainly formulate them successfully. Unfortunately, there is no quick and easy way to learn how to build evidence. You need a solid foundation in your subject knowledge to come up with the correct propositions and definitions for logically developing your evidence. By reading examples and practicing yourself, you will be able to master the skills of mathematical proofing.

To step

Method 1 of 3: Understanding the problem

Understand the question. You must first determine exactly what it is that you are trying to prove. This question will also serve as the final thesis of the evidence. In this step you will also define the assumptions you will be working with. Identifying the question and making the necessary assumptions gives you a starting point for understanding the problem and developing the evidence.
Draw diagrams. When trying to understand the inner workings of a math problem, it is sometimes easiest to draw a diagram of what is happening. Charts are particularly important in geometric proofs because they allow you to visualize what you actually want to prove.
- Use the information provided in the problem to draw a picture of the evidence. Name the acquaintances and strangers.
- When working out the evidence, use the necessary information to support the evidence.
Study evidence of related theorems. Evidence is difficult to learn to construct, but an excellent way to learn this is to study related statements and how they were proven.
- Realize that proof is just a good argument where every step is substantiated. You can find a lot of evidence to study, both online and in a textbook.
Ask questions. It is very normal to get stuck in a proof. Ask your teacher or classmates if you can't figure it out. The latter may have similar questions and you can work together on the issues. It is better to ask questions and then understand than to wade blindly through the evidence.
- Consult with your teacher after class for additional explanation.

Method 2 of 3: Structuring a proof

Define mathematical proofs. A mathematical proof is a set of logical statements supported by theorems and definitions that prove the correctness of another mathematical statement. Proofs are the only way to know if a statement is mathematically valid.
- Being able to formulate a mathematical proof indicates a fundamental understanding of the problem itself, and all of the concepts involved in the problem.
- Evidence also forces you to look at math in a new and exciting way. Just by trying to prove something will give you more knowledge and insight about it, even if your evidence doesn't seem to add up in the end.
Know your audience. Before writing a proof, you have to think about the audience you are writing it for and what they already know. If you write proof for a publication, you will do it differently than for a high school class.
- Knowing your audience allows you to formulate the evidence in a way that it will understand given the amount of background knowledge the audience has.
Understand the type of evidence you are putting forward. There are a few different types of proof, and the one you choose depends on your target audience and the assignment. If you are unsure which version to use, ask your teacher for advice. In high school, you may be expected to formulate the evidence in a specific format, such as a two-column formal proof.
- A two-column proof is a structure where data and assertions are placed in one column and the supporting evidence next to it in a second column. They are very often used in geometry.
- Informal paragraph proof uses grammatically correct statements and fewer symbols. At a higher level you should always use an informal proof.
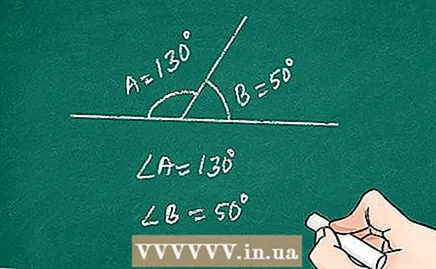
Write the proof in two columns as an overview. Structuring a proof in two columns is an easy way to organize your thoughts and consider the problem. Draw a line down the center of the page and write all the data and statements on the left. Write the corresponding definitions / statements to the right, next to the data they support.
- For instance:
- Angle A and angle B form a linear pair. Given.
- Corner ABC is straight. Definition of a right angle.
- Angle ABC is 180 °. Definition of a line.
- Angle A + angle B = angle ABC. Postulate for adding angles.
- Angle A + angle B = 180 °. Substitution.
- Angle A as a supplement to angle B. Definition of additional angles.
- Q.E.D.
Convert the proof in two columns to an informal proof. Based on the proof in two columns, write an informal proof as a paragraph without too many symbols and abbreviations.
- For example, let's say angle A and B are linear pairs. The hypothesis is that angle A and angle B complement each other (are supplementary). Angle A and angle B form a straight line because they are linear pairs. A straight line is defined as an angle of 180 °. Given the postulate for the addition of angles, angles A and B together form the line ABC. By way of substitution, A and B together are 180 °, therefore they are supplementary angles. Q.E.D.

Method 3 of 3: Formulating the evidence

Learn the vocabulary of mathematical proof. There are certain statements and sentences that you keep seeing in a mathematical proof. These are the phrases you should be familiar with and be able to use well when formulating your own evidence.
- "If A, then B" means that you must show that if A is true, B must also be true.
- "A if and only if B" means that you must prove that A and B are true and false at the same time. Prove both "If A, then B" and "if not A, then not B".
- "A only if B" means the same as "If A, then B", so it is not often used. It's good to be aware of this when you come across it.
- When making the evidence, you should avoid using "I" in favor of "we".
Write down all the information. When putting together a proof, the first step is to identify and record all data. This is the best place to start as it will help you think about what is known and what information you need to complete the evidence. Read the problem and write down each piece of information.
- For example: Prove that two angles that form a linear pair (angle A and angle B) are supplementary.
- Given: angle A and angle B form a linear pair
- Proof: angle A is supplementary to angle B.
Define all variables. In addition to writing the data, it is useful to define all variables. Write the definitions at the beginning of the evidence to avoid confusion for the reader. If variables are not defined, a reader can easily get lost trying to understand your evidence.
- Do not use variables in your proof that have not yet been defined.
- For example: Variables are the measures of angle A and angle B.
Work backwards through the evidence. It is often easiest to think backward about a problem. Start with the conclusion, what you are trying to prove, and think about the steps that can lead you back to the beginning.
- Edit the steps at the beginning and end to see if they are similar. Use the data, definitions you have learned and similar evidence.
- Ask yourself questions along the way. "Why is this so?" And "Is there any way this is false?" Are good questions for any statement or claim.
- Don't forget to write the steps in sequence for the final proof.
- For example: If angles A and B are supplementary, then together they must be 180 °. The two corners together form the line ABC. You know that they form a line because of the definition of linear pairs. Since a straight line is 180 °, you can use substitution to prove that angle A and angle B add up to 180 °.
Place your steps in logical order. Start the evidence at the beginning and work your way up to the conclusion. While it is helpful to think about the evidence, by starting with the conclusion and working backwards, when presenting the actual evidence, you will put the conclusion at the end. The statements in the evidence should flow from each other, with substantiation for each statement, so that there is no reason to doubt the validity of your evidence.
- Start by listing the assumptions you are working with.
- Divide them into simple and clear steps so that the reader does not have to wonder how one step logically flows from another.
- It is not uncommon to formulate multiple proofs of concept. Keep rearranging until all steps are in the most logical order.
- For example: start at the beginning.
  - Angle A and angle B form a linear pair.
  - Corner ABC is straight.
  - Angle ABC is 180 °.
  - Angle A + angle B = angle ABC.
  - Angle A + angle B = 180 °.
  - Angle A is supplementary to angle B.
Avoid using arrows and abbreviations in the written evidence. When outlining the plan for your proof, you can use shorthand and symbols, but when writing the final proof, symbols, such as arrows, can confuse the reader. Instead, use words like "then" or "so".
- Exceptions for using abbreviations are: e.g. (for example) and i.e. (i.e.), but make sure you use them correctly.
Support all statements with a theorem (theorem), law or definition. Evidence is only as good as the evidence used. You cannot make a statement without substantiating it with a definition. Refer to other similar evidence as an example.
- Try to apply your evidence to a case where the false must be, and verify that this is actually the case. If the result is not false, adjust the proof so that it is.
- Many geometric proofs are written as a two-column proof, with the statement and the proof. A formal mathematical proof intended for publication is written as a paragraph with correct grammar.
End it with a conclusion or Q.E.D. The final statement of evidence must be the hypothesis you were trying to prove. Once you've made this statement, close the proof with a final symbol, such as Q.E.D. or a solid square, to indicate that the proof is complete.
- Q.E.D. stands for "quod erat demonstrandum" (Latin for "that which had to be proved").
- If you are not sure if your evidence is correct, just write in a few sentences what your conclusion is and why it is significant.