Content

• To step
• Method 1 of 2: Test the algebraically function
• Tips
• Warning

One way to classify functions is either as "even", "odd", or as neither. These terms refer to the repetition or symmetry of the function. The best way to find this out is to manipulate the function algebraically. You can also study the graph of the function and look for symmetry. Once you know how to classify functions, you can also predict the appearance of certain combinations of functions.

To step

Method 1 of 2: Test the algebraically function

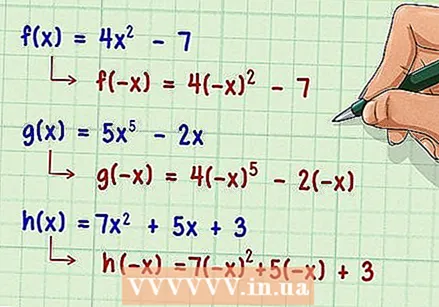1. View inverted variables. In algebra, the inverse of a variable is negative. This is true or the variable of the function now ${ displaystyle x}$Replace each variable of the function with its inverse. Do not change anything else on the original function, except the sign. For instance:
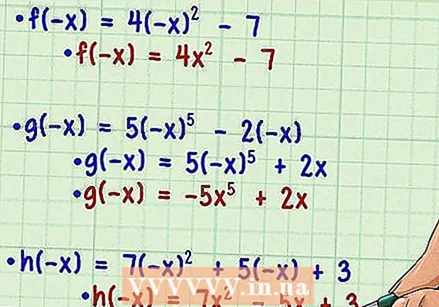   • ${ displaystyle f (x) = 4x ^ {2} -7}$Simplify the new function. At this point, you don't have to worry about solving the function for any given numeric value. You just simplify the variables to compare the new function, f (-x), with the original function, f (x). Recall the ground rules of exponents that say that a negative base to an even power will be positive, while a negative base will be negative to an odd power.
     • ${ displaystyle f (-x) = 4 (-x) ^ {2} -7}$Compare the two functions. For every example you try, compare the simplified version of f (-x) with the original f (x). Place the terms side by side for easy comparison, and compare the signs of all terms.
       • If the two results are the same, then f (x) = f (-x), and the original function is even. An example is:
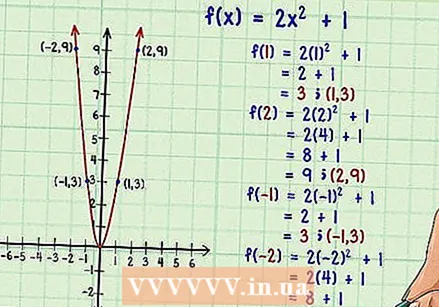         • ${ displaystyle f (x) = 4x ^ {2} -7}$Graph the function. Use graph paper or a graphing calculator to graph the function. Choose different numeric values ​​for it 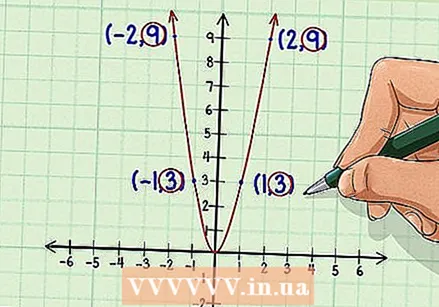${ displaystyle x}$Note symmetry along the y axis. When looking at a function, symmetry will suggest a mirror image. If you see that the part of the graph on the right (positive) side of the y axis matches the part of the graph on the left (negative) side of the y axis, then the graph is symmetrical about the y axis. ash. If a function is symmetrical about the y-axis, then the function is even.
           • You can test for symmetry by selecting individual points.If the y value of any x value is the same as the y value of -x, then the function is even. The points chosen above for plotting 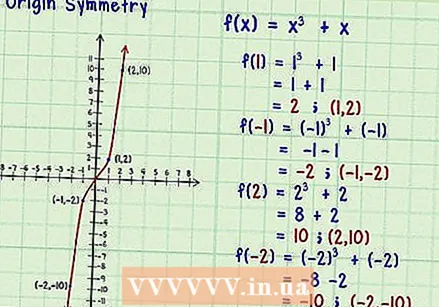${ displaystyle f (x) = 2x ^ {2} +1}$Test for symmetry from the origin. The origin is the central point (0,0). Origin symmetry means that a positive result for a chosen x value will correspond to a negative result for -x, and vice versa. Odd functions show origin symmetry.
             • If you choose a pair of test values ​​for x and their inverse corresponding values ​​for -x, you should get inverse results. Consider the function 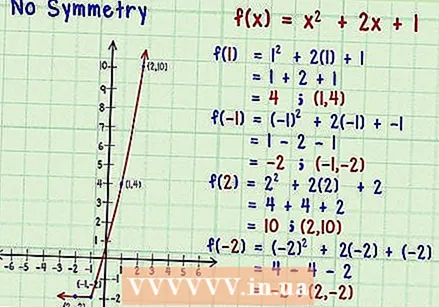${ displaystyle f (x) = x ^ {3} + x}$See if there is no symmetry. The last example is a function without symmetry on both sides. If you look at the graph you will see that it is not a mirror image on either the y axis or around the origin. Check out the feature ${ displaystyle f (x) = x ^ {2} + 2x + 1}$.
               • Choose a few values ​​for x and -x, as follows:
                 • ${ displaystyle f (1) = 1 ^ {2} +2 (1) + 1 = 1 + 2 + 1 = 4}$. The point to plot is (1,4).
                 • ${ displaystyle f (-1) = (- 1) ^ {2} +2 (-1) + (- 1) = 1-2-1 = -2}$. The point to plot is (-1, -2).
                 • ${ displaystyle f (2) = 2 ^ {2} +2 (2) + 2 = 4 + 4 + 2 = 10}$. The point to plot is (2,10).
                 • ${ displaystyle f (-2) = (- 2) ^ {2} +2 (-2) + (- 2) = 4-4-2 = -2}$. The point to plot is (2, -2).
               • This already gives you enough points to notice that there is no symmetry. The y values ​​for opposite pairs of x values ​​are not the same, nor are they the opposite of each other. This function is neither even nor odd.
               • You may see that this feature, ${ displaystyle f (x) = x ^ {2} + 2x + 1}$, can be rewritten as ${ displaystyle f (x) = (x + 1) ^ {2}}$. Written in this form, it looks like it is an even function because there is only one exponent, which is an even number. However, this example illustrates that you cannot determine whether a function is even or odd when it is enclosed in parentheses. You have to elaborate the function in separate terms and then examine the exponents.

Tips

• If all forms of a variable in the function have even exponents, then the function is even. If all exponents are odd, then the function is odd overall.

Warning

• This article applies only to functions with two variables, which can be graphed in a two-dimensional coordinate system.