Content

• To step
• Method 1 of 3: Using the substitution method
• Method 2 of 3: Using the elimination method
• Method 3 of 3: Graph the equations
• Tips
• Warnings

In a "system of equations" you are asked to solve two or more equations at the same time. When these two contain different variables, such as x and y, or a and b, it can be difficult at first glance to see how to solve them. Fortunately, once you know what to do, you only need some basic math skills (and sometimes some fraction knowledge) to solve the problem. If required, or if you are a visual student, learn how to graph the equations as well. Graphing (plotting) a graph can be useful to "see what's going on," or to check your work, but it can also be slower than the other methods and it doesn't work with all equation systems.

To step

Method 1 of 3: Using the substitution method

1. Move the variables to different sides of the equation. This "substitution" method begins with "solving for x" (or any other variable) in one of the equations. For example, we have the following equations: 4x + 2y = 8 and 5x + 3x = 9. First of all, we look at the first comparison. Rearrange by subtracting 2y from each side, and you get: 4x = 8-2y.
   • This method often uses fractions at a later stage. You can also use the elimination method below if you prefer not to work with fractions.
2. Divide both sides of the equation to solve for "x". Once you have the term x (or whatever variable you use) on one side of the equation, divide both sides of the equation to isolate the variable. For instance:
   • 4x = 8-2y
   • (4x) / 4 = (8/4) - (2y / 4)
   • x = 2 - ½y
3. Plug this back into the other equation. Make sure to return to the Others comparison, not the one you've already used. In that equation, you replace the variable you solved, leaving only one variable. For instance:
   • You now know that: x = 2 - ½y.
   • The second equation, which you haven't changed yet, is: 5x + 3x = 9.
   • In the second equation, replace x with "2 - ½y": 5 (2 - ½y) + 3y = 9.
4. Solve for the remaining variable. You now have an equation with only one variable. Use common algebra techniques to solve for that variable. If the variables cancel each other out, skip to the last step. Otherwise, you end up with an answer to one of your variables:
   • 5 (2 - ½y) + 3y = 9
   • 10 - (5/2) y + 3y = 9
   • 10 - (5/2) y + (6/2) y = 9 (If you don't understand this step, learn how to add fractions. This is often, but not always, necessary with this method).
   • 10 + ½y = 9
   • ½y = -1
   • y = -2
5. Use the answer to solve for the other variable. Don't make the mistake of finishing the problem halfway through. You will have to re-enter the answer you got into one of the original equations so that you can solve for the other variable:
   • You now know that: y = -2
   • One of the original equations is: 4x + 2y = 8. (Both equations can be used for this step).
   • Plug in -2 instead of y: 4x + 2 (-2) = 8.
   • 4x - 4 = 8
   • 4x = 12
   • x = 3
6. Know what to do if both variables cancel each other out. When you x = 3y + 2 or get a similar answer in the other equation, you're trying to get an equation with only one variable. Sometimes you end up with an equation instead without variables. Double check your work, and make sure to substitute the (rearranged) first equation in the second equation, and not the first equation. If you are sure you have not made any mistakes, you will get one of the following results:
   • If you end up with an equation with no variables and which is not true (e.g. 3 = 5), then you have the problem no solution. (If you have graphed the equations, you will see that they are parallel and never intersect).
   • If you end up with an equation without variables, but those well is true (for example 3 = 3), then it has the problem an infinite number of solutions. The two equations are exactly equal. (If you graph the two equations, you will see that they overlap exactly).

Method 2 of 3: Using the elimination method

1. Determines the variable to be eliminated. Sometimes the equations will "eliminate" each other in a variable as soon as you add them together. For example, when you do the equations 3x + 2y = 11 and 5x - 2y = 13 combines, the "+ 2y" and "-2y" will cancel each other out, with all of the "ys are eliminated from the equation. Look at the equations in your problem to find out if any of the variables will be eliminated in this way. If none of the variables are eliminated, read on to the next step for advice.
2. Multiply an equation to cancel out a variable. (Skip this step if the variables have already eliminated each other). If none of the variables in the equations cancel out by itself, then you have to change one of the equations so that it does. This is easiest to understand with an example:
   • Suppose you have the system of equations 3x - y = 3 and -x + 2y = 4.
   • Let's change the first equation so that the variable is y is eliminated. (You can also do this for X do and get the same answer).
   • The - y " of the first equation should be eliminated with the + 2y In the second equation. We can do this through - y multiply by 2.
   • We multiply both sides of the first equation by 2, as follows: 2 (3x - y) = 2 (3), and thus 6x - 2y = 6. Now will - 2y fall away against the + 2y in the second equation.
3. Combine the two equations. To be able to combine two equations, add the left and right sides together. If you have written the equation correctly, one of the variables should cancel out against the other. Here's an example using the same equations as the last step:
   • Your equations are: 6x - 2y = 6 and -x + 2y = 4.
   • Combine the left sides: 6x - 2y - x + 2y =?
   • Combine the right sides: 6x - 2y - x + 2y = 6 + 4.
4. Solve for the last variable. Simplify the combined equation and then use basic algebra to solve for the last variable. If there are no variables left after simplification, continue to the last step in this section. Otherwise, you should end with a simple answer to one of your variables. For instance:
   • You have: 6x - 2y - x + 2y = 6 + 4.
   • Group the variables X and y with each other: 6x - x - 2y + 2y = 6 + 4.
   • Simplify: 5x = 10
   • Solve for x: (5x) / 5 = 10/5, so that x = 2.
5. Solve for the other variables. You have found one variable, but you are not quite done yet. Substitute your answer in one of the original equations so that you can solve for the other variable. For instance:
   • You know that x = 2, and that one of your original equations 3x - y = 3 is.
   • Plug 2 in, instead of x: 3 (2) - y = 3.
   • Solve y in the equation: 6 - y = 3
   • 6 - y + y = 3 + y, so 6 = 3 + y
   • 3 = y
6. Know what to do when both variables cancel each other out. Sometimes combining two equations results in an equation that has no meaning or does not help you solve the problem. Double check your work from the beginning, but if you didn't make a mistake, write down one of the following answers:
   • If your combined equation has no variables and is not true (like 2 = 7) then there is no solution which holds for both equations. (If you graph both equations, you will see that they are parallel and never intersect).
   • If your combined equation has no variables and is true (such as 0 = 0), then there are an infinite number of solutions. The two equations are actually identical. (If you place these in a graph, you see that they completely overlap each other).

Method 3 of 3: Graph the equations

1. Only use this method when specified. Unless you are using a computer or a graphing calculator, many systems of equations can only be approximately solved using this method. Your teacher or math textbook may ask you to use this method, so you are probably familiar with graphical equations such as lines. You can also use this method to check if your answers from any of the other methods are correct.
   • The basic idea is that you graph both equations and determine the point where they intersect. The x and y values ​​at this point return the value of x and the value of y in the system of equations.
2. Solve both equations for y. Keep the two equations separate, and use algebra to convert each equation to the form "y = __x + __". For instance:
   • The first equation is: 2x + y = 5. Change this to: y = -2x + 5.
   • The second equation is: -3x + 6y = 0. Change this to 6y = 3x + 0, and simplify to y = ½x + 0.
   • Are both equations identical, then the entire line becomes an "intersection point". Write: infinite solutions.
3. Draw a coordinate system. Draw a vertical "y-axis" and a horizontal "x-axis" on a sheet of graph paper. Start at the point where the lines intersect, and label the numbers 1, 2, 3, 4, etc. up the y axis and right again along the x axis. Label the numbers -1, -2, etc. down the y axis and to the left along the x axis.
   • If you don't have graph paper, use a ruler to make sure the numbers are evenly spaced.
   • If you're using large numbers or decimal places, you may need to scale the chart. (For example 10, 20, 30 or 0.1, 0.2, 0.3 instead of 1, 2, 3).
4. Draw the y intersection for each line. Once you have an equation in the form y = __x + __ you can start graphing it by setting up a point where the line intercepts the y-axis. This is always at a y value, equal to the last number in this equation.
   • In the previously mentioned examples, one line (y = -2x + 5) into the y-axis 5. The other line (y = ½x + 0) passes through the zero point 0. (These are points (0.5) and (0.0) in the graph).
   • Indicate each of the lines with a different color, if possible.
5. Use the slope to continue drawing the lines. In the form y = __x + __, is the number for x th slope off the line. Each time x is increased by one, the y value will increase with the value of the slope. Use this information to find the point on the graph for each line when x = 1. (Alternatively, substitute x = 1 for each equation and solve for y).
   • In our example, the line has y = -2x + 5 a slope of -2. At x = 1 the line 2 descends down from the point x = 0. Draw the line segment between (0.5) and (1.3).
   • The rule y = ½x + 0has a slope of ½. At x = 1, the line goes ½ up from the point x = 0. Draw the line segment between (0,0) and (1, ½).
   • When the lines have the same slope the lines will never intersect, so there is no solution for the system of equations. Write: no solution.
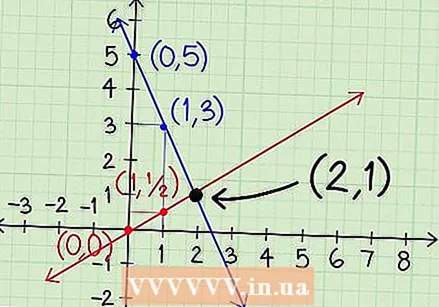6. Continue plotting the lines until they intersect. Stop and look at your chart. If the lines have already crossed each other, move on to the next step. Otherwise, you make a decision based on what the lines do:
   • As the lines move towards each other, you keep drawing points in that direction.
   • If the lines are moving away from each other, go back and draw points in the other direction, starting at x = -1.
   • If the lines are nowhere close to each other, jump ahead and plot more distant points, such as x = 10.
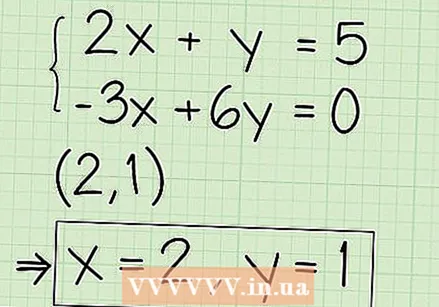7. Find the answer at the intersection of the lines. Once the two lines intersect, the x and y values ​​at that point are the solution to the problem. If you are lucky, the answer will be an integer. For example, in our examples, the two lines intersect (2,1) so is your answer x = 2 and y = 1. In some systems of equation, the lines will intersect at a value between two integers, and unless your graph is extremely accurate it will be difficult to tell where this is. If this is the case, you can give an answer like: "x is between 1 and 2". You can also use the substitution method or elimination method to find the exact answer.

Tips

• You can check your work by entering the answers back into the original equations. If the equations are true (for example, 3 = 3), then your answer is correct.
• In the elimination method, you sometimes have to multiply an equation by a negative number to eliminate a variable.

Warnings

• These methods cannot be used if you are dealing with a power number, such as x. To learn more about equations of this type, you'll need a guide to factor squaring with two variables.