Content

• To step
• Part 1 of 2: Understanding how it works
• Part 2 of 2: Dividing fractions by fractions - examples

Dividing a fraction by a fraction can seem a bit confusing at first, but it's really easy. All you have to do is reverse the bottom or second fraction and then multiply both fractions! This article will show you how to do this and will show you that dividing fractions by fractions shouldn't be a problem at all.

To step

Part 1 of 2: Understanding how it works

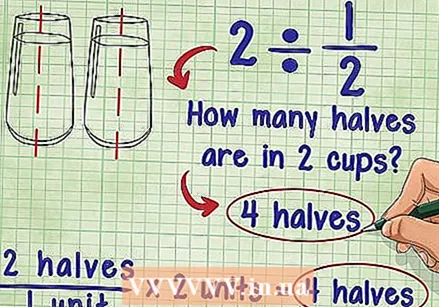1. Think about what dividing by a fraction is. The exercise 2 ÷ 1/2 says the same as: "How often does ½ go into 2?" The answer is 4, because you can divide 2 into 4 halves.
   • Also try to think about this problem in terms of glasses of water: How many half glasses of water are there in 2 glasses of water? You can solve this by pouring 2 half glasses of water into another glass, so that you eventually have 2 full glasses of water: 2 half / 1 glass * 2 glasses = 4 half glasses.
   • This means that if you divide a number by a number between 0 and 1, the answer will always be greater than that number! This is true whether you divide an integer or fraction by another fraction.
2. Sharing is the opposite of multiplication. So you can also think of dividing by a fraction as multiplying by the reciprocal of that fraction. The reverse of a fraction is what it says, simply swapping the numerator and denominator. In a moment we're going to divide fractions by fractions using multiplication by the inverse of the denominator, but now let's take a look at some inversions of fractions first:
   • The reverse of 3/4 is 4/3.
   • The reverse of 7/5 is 5/7.
   • The reciprocal of 1/2 is 2/1, so 2.
3. Remember the following steps for dividing a fraction by another fraction. In order these are the steps:
   • Leave the counter unchanged.
   • Make a multiplication of the division sign.
   • Make the reverse of the second fraction.
   • Multiply the numerators of the two fractions. The result will be the counter of your answer.
   • Multiply the denominators of the two fractions. The result becomes the denominator of your answer.
   • Simplify the fraction.
4. Follow these steps in the example 1/3 ÷ 2/5. We leave the numerator (the first fraction) unchanged and change the division sign to a go sign:
   • 1/3 ÷ 2/5 = is becoming:
   • 1/3 * __ =
   • Now we turn the second fraction (2/5). This then becomes 5/2:
   • 1/3 * 5/2 =
   • Now we're multiplying the numerators of the two fractions, 1 * 5 = 5.
   • 1/3 * 5/2 = 5/
   • Now we multiply the denominators of the two fractions, 3 * 2 = 6.
   • We now have: 1/3 * 5/2 = 5/6
   • This particular fraction cannot be simplified further, so we now have our answer.
5. Try to remember the following:"Dividing by a fraction is the same as multiplying by the reverse."

Part 2 of 2: Dividing fractions by fractions - examples

1. Start with an example problem. Suppose we have the problem 2/3 ÷ 3/7. The question here is how often 3/7 fits into 2/3. Do not panic; it's not as hard as it sounds!
2. Make the division sign a multiplication sign. The statement now becomes: 2/3 * __ (we'll fill in the empty field in a moment.)
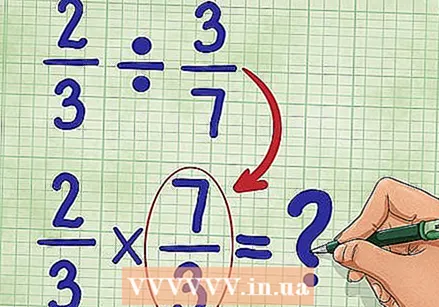3. Now we determine the inverse of the second fraction. This means we flip 3/7 so that the numerator becomes 3 and the denominator becomes 7. The inverse of 3/7 is 7/3. Now we note the new statement:
   • 2/3 * 7/3 = __
4. Multiply the fractions. First, we multiply the numerators of the two fractions: 2 * 7 = 14.14 is the counter of your answer. Then we multiply the denominators of the two fractions: 3 * 3 = 9.9 is the denominator of your answer. Now you know that 2/3 * 7/3 = 14/9.
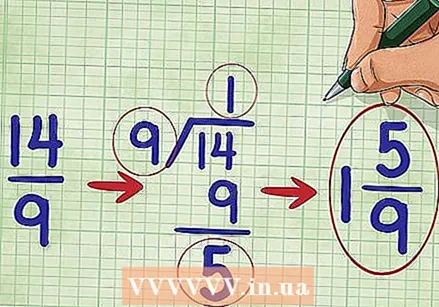5. Simplify the fraction. In this case, because the numerator of the fraction is greater than the denominator, we know that the fraction is greater than 1, and we should convert it to a mixed number. (A mixed number is an integer with a fraction, such as 1 2/3.)
   • First, divide the counter 14 through 9. 9 goes into 14 once, with a remainder of 5, so you can write this as: 1 5/9.
   • You can stop now because you have found the answer! You can see that this fraction cannot be simplified further, because 9 is not completely divisible by 5 and because the numerator is prime.
6. We try one more example! Suppose we have the following problem 4/5 ÷ 2/6 =. First, change the division sign to a multiplication sign (4/5 * __ = ), then you determine the inverse of 2/6, which is 6/2. Now the problem is as follows: 4/5 * 6/2 =__. Now we multiply the counters, 4 * 6 = 24, and denominators 5* 2 = 10. Now we have the following:4/5 * 6/2 = 24/10. Simplify the fraction. Since the numerator is greater than the denominator, we will have to convert this to a mixed fraction.
   • First divide the numerator by the denominator, (24/10 = 2 remainder 4).
   • Write the answer as 2 4/10. But we can simplify this fraction even more!
   • Note that 4 and 10 are both even numbers, so the first step is to simplify it by dividing them both by 2. The fraction is now 2/5.
   • Because the denominator (5) does not completely fit into the numerator (2), and is also a prime number, you know that you cannot simplify this fraction further. So the answer is: 2 2/5.
7. Find more information about simplifying fractions. You may have learned all of that before, but it never hurts to refresh all that faded knowledge. Various articles can be found on the internet to further improve those skills.