Content

• Steps
• Part 1 of 3: Average
• Part 2 of 3: Dispersion
• Part 3 of 3: Standard deviation

By calculating the standard deviation, you will find the spread in the sample data. But first, you have to compute some quantities: the mean and variance of the sample. Variance is a measure of the spread of data around the mean. The standard deviation is equal to the square root of the sample variance. This article will show you how to find the mean, variance, and standard deviation.

Steps

Part 1 of 3: Average

1. 1 Take a dataset. Average is an important quantity in statistical calculations.
   • Determine the number of numbers in the dataset.
   • Are the numbers in the set very different from each other or are they very close (differ by fractional parts)?
   • What do the numbers in the dataset represent? Test scores, heart rate, height, weight and so on.
   • For example, a set of test scores: 10, 8, 10, 8, 8, 4.
2. 2 To calculate the average, you need all the numbers in a given dataset.
   • The mean is the average of all numbers in the dataset.
   • To calculate the average, add all the numbers in your dataset and divide the resulting value by the total number of numbers in the dataset (n).
   • In our example (10, 8, 10, 8, 8, 4) n = 6.
3. 3 Add up all the numbers in your dataset.
   • In our example, the numbers are: 10, 8, 10, 8, 8, and 4.
   • 10 + 8 + 10 + 8 + 8 + 4 = 48. This is the sum of all the numbers in the dataset.
   • Add the numbers again to check your answer.
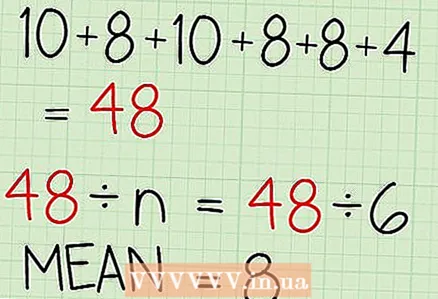4. 4 Divide the sum of the numbers by the number of numbers (n) in the sample. You will find the average.
   • In our example (10, 8, 10, 8, 8 and 4) n = 6.
   • In our example, the sum of the numbers is 48. So divide 48 by n.
   • 48/6 = 8
   • The average value of this sample is 8.

Part 2 of 3: Dispersion

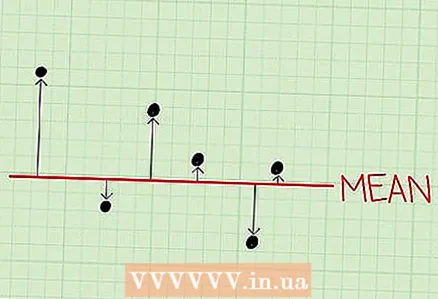1. 1 Calculate the variance. It is a measure of the dispersion of the data around the mean.
   • This value will give you an idea of ​​how the sample data is scattered.
   • The low variance sample includes data that is not much different from the mean.
   • A sample with high variance includes data that is very different from the mean.
   • Variance is often used to compare the distribution of two data sets.
2. 2 Subtract the average from each number in the dataset. You will find out how much each value in the dataset differs from the mean.
   • In our example (10, 8, 10, 8, 8, 4) the average is 8.
   • 10 - 8 = 2; 8 - 8 = 0, 10 - 2 = 8, 8 - 8 = 0, 8 - 8 = 0, and 4 - 8 = -4.
   • Do the subtraction again to check each answer. This is very important, as these values ​​will be needed when calculating other quantities.
3. 3 Square each value you got in the previous step.
   • Subtracting the mean (8) from each number in the sample (10, 8, 10, 8, 8, and 4) gives you the following values: 2, 0, 2, 0, 0, and -4.
   • Square these values: 2, 0, 2, 0, 0, and (-4) = 4, 0, 4, 0, 0, and 16.
   • Check the answers before proceeding to the next step.
4. 4 Add the squares of the values, that is, find the sum of squares.
   • In our example, the squares of the values ​​are 4, 0, 4, 0, 0, and 16.
   • Recall that the values ​​are obtained by subtracting the mean from each sample number: (10-8) ^ 2 + (8-8) ^ 2 + (10-2) ^ 2 + (8-8) ^ 2 + (8-8 ) ^ 2 + (4-8) ^ 2
   • 4 + 0 + 4 + 0 + 0 + 16 = 24.
   • The sum of the squares is 24.
5. 5 Divide the sum of squares by (n-1). Remember, n is the amount of data (numbers) in your sample. This way you get the variance.
   • In our example (10, 8, 10, 8, 8, 4) n = 6.
   • n-1 = 5.
   • In our example, the sum of squares is 24.
   • 24/5 = 4,8
   • The variance of this sample is 4.8.

Part 3 of 3: Standard deviation

1. 1 Find the variance to calculate the standard deviation.
   • Remember that variance is a measure of how much the data is spread out around the mean.
   • The standard deviation is a similar quantity that describes the distribution of data in a sample.
   • In our example, the variance is 4.8.
2. 2 Take the square root of the variance to find the standard deviation.
   • Typically, 68% of all data is within one standard deviation of the mean.
   • In our example, the variance is 4.8.
   • √4.8 = 2.19. The standard deviation of this sample is 2.19.
   • 5 out of 6 numbers (83%) of this sample (10, 8, 10, 8, 8, 4) are within one standard deviation (2.19) from the mean (8).
3. 3 Check that the mean, variance and standard deviation are calculated correctly. This will allow you to verify your answer.
   • Be sure to write down your calculations.
   • If you get a different value while checking the calculations, check all calculations from the beginning.
   • If you can't find where you made a mistake, do the calculations from the beginning.