Content

• Steps
• Method 1 of 3: How to find the unknown side
• Method 2 of 3: Finding an Unknown Angle
• Method 3 of 3: Sample Problems
• Tips

The cosine theorem is widely used in trigonometry. It is used when working with irregular triangles to find unknown quantities such as sides and angles. The theorem is similar to the Pythagorean theorem and is fairly easy to remember. The cosine theorem says that in any triangle ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$.

Steps

Method 1 of 3: How to find the unknown side

1. 1 Write down the known values. To find the unknown side of a triangle, you need to know the other two sides and the angle between them.
   • For example, given a triangle XYZ. The YX side is 5 cm, the YZ side is 9 cm, and the Y angle is 89 °. What is the XZ side?
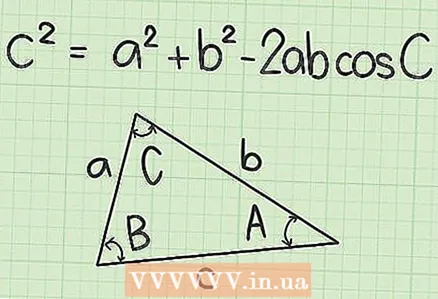2. 2 Write down the cosine theorem formula. Formula: ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$, where ${ displaystyle c}$ - unknown party, ${ displaystyle cos {C}}$ - cosine of the angle opposite to the unknown side, ${ displaystyle a}$ and ${ displaystyle b}$ - two well-known sides.
3. 3 Plug the known values ​​into the formula. Variables ${ displaystyle a}$ and ${ displaystyle b}$ denote two known sides. Variable ${ displaystyle C}$ is the known angle that lies between the sides ${ displaystyle a}$ and ${ displaystyle b}$.
   • In our example, the XZ side is unknown, so in the formula it is denoted as ${ displaystyle c}$... Since the sides YX and YZ are known, they are denoted by the variables ${ displaystyle a}$ and ${ displaystyle b}$... Variable ${ displaystyle C}$ is the angle Y. So, the formula will be written as follows: ${ displaystyle c ^ {2} = 5 ^ {2} + 9 ^ {2} -2 (5) (9) cos {89}}$.
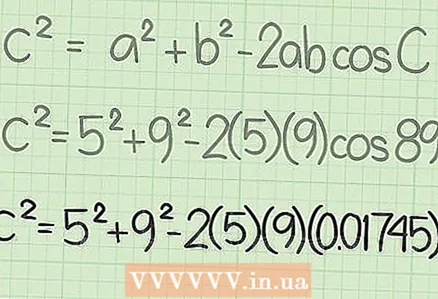4. 4 Find the cosine of a known angle. Do it with a calculator. Enter an angle value, and then click ${ displaystyle COS}$... If you don't have a scientific calculator, find an online cosine table, for example, here. Also in Yandex, you can enter "cosine of X degrees" (substitute the angle value for X), and the search engine will display the cosine of the angle.
   • For example, the cosine is 89 ° ≈ 0.01745. So: ${ displaystyle c ^ {2} = 5 ^ {2} + 9 ^ {2} -2 (5) (9) (0.01745)}$.
5. 5 Multiply the numbers. Multiply ${ displaystyle 2ab}$ by the cosine of a known angle.
   • For example:
     ${ displaystyle c ^ {2} = 5 ^ {2} + 9 ^ {2} -2 (5) (9) (0.01745)}$
     ${ displaystyle c ^ {2} = 5 ^ {2} + 9 ^ {2} -1.5707}$
6. 6 Fold the squares of the known sides. Remember, to square a number, it must be multiplied by itself. First, square the corresponding numbers, and then add the resulting values.
   • For example:
     ${ displaystyle c ^ {2} = 5 ^ {2} + 9 ^ {2} -1.5707}$
     ${ displaystyle c ^ {2} = 25 + 81-1.5707}$
     ${ displaystyle c ^ {2} = 106-1.5707}$
7. 7 Subtract two numbers. You will find ${ displaystyle c ^ {2}}$.
   • For example:
     ${ displaystyle c ^ {2} = 106-1.5707}$
     ${ displaystyle c ^ {2} = 104.4293}$
8. 8 Take the square root of this value. To do this, use a calculator. This is how you find the unknown side.
   • For example:
     ${ displaystyle c ^ {2} = 104.4293}$
     ${ displaystyle { sqrt {c ^ {2}}} = { sqrt {104.4293}}}$
     ${ displaystyle c = 10.2191}$
     So, the unknown side is 10.2191 cm.

Method 2 of 3: Finding an Unknown Angle

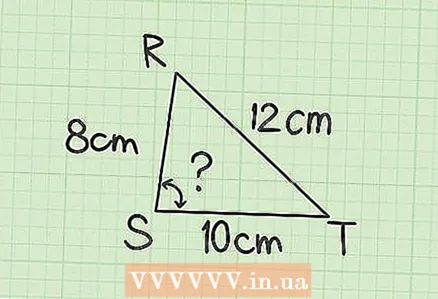1. 1 Write down the known values. To find the unknown angle of a triangle, you need to know all three sides of the triangle.
   • For example, given a triangle RST. Side CP = 8 cm, ST = 10 cm, PT = 12 cm.Find the value of the angle S.
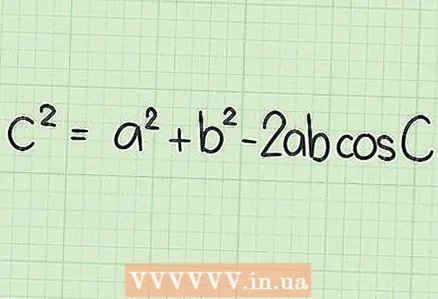2. 2 Write down the cosine theorem formula. Formula: ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$, where ${ displaystyle cos {C}}$ - cosine of an unknown angle, ${ displaystyle c}$ - a known side opposite an unknown corner, ${ displaystyle a}$ and ${ displaystyle b}$ - two other famous parties.
3. 3 Find the values a{ displaystyle a}, b{ displaystyle b} and c{ displaystyle c}. Then plug them into the formula.
   • For example, the RT side is opposite to the unknown angle S, so the RT side is ${ displaystyle c}$ in the formula. Other parties will ${ displaystyle a}$ and ${ displaystyle b}$... So, the formula will be written as follows: ${ displaystyle 12 ^ {2} = 8 ^ {2} + 10 ^ {2} -2 (8) (10) cos {C}}$.
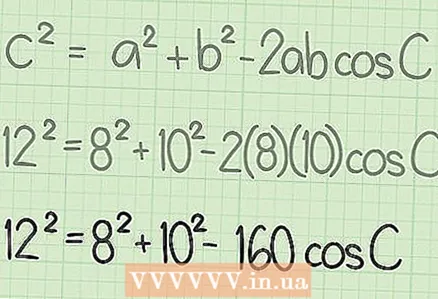4. 4 Multiply the numbers. Multiply ${ displaystyle 2ab}$ by the cosine of the unknown angle.
   • For example, ${ displaystyle 12 ^ {2} = 8 ^ {2} + 10 ^ {2} -160 cos {C}}$.
5. 5 Erect c{ displaystyle c} in a square. That is, multiply the number itself.
   • For example, ${ displaystyle 144 = 8 ^ {2} + 10 ^ {2} -160 cos {C}}$
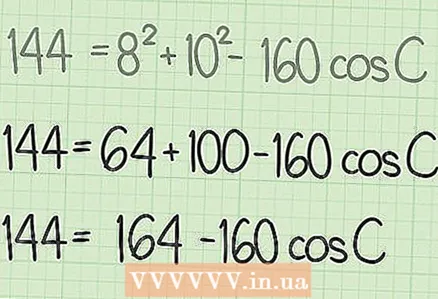6. 6 Fold the squares a{ displaystyle a} and b{ displaystyle b}. But first, square the corresponding numbers.
   • For example:
     ${ displaystyle 144 = 64 + 100-160 cos {C}}$
     ${ displaystyle 144 = 164-160 cos {C}}$
7. 7 Isolate the cosine of the unknown angle. To do this, subtract the amount ${ displaystyle a ^ {2}}$ and ${ displaystyle b ^ {2}}$ from both sides of the equation. Then divide each side of the equation by the factor at the cosine of the unknown angle.
   • For example, to isolate the cosine of an unknown angle, subtract 164 from both sides of the equation, and then divide each side by -160:
     ${ displaystyle 144-164 = 164-164-160 cos {C}}$
     ${ displaystyle -20 = -160 cos {C}}$
     ${ displaystyle { frac {-20} {- 160}} = { frac {-160 cos {C}} {- 160}}}$
     ${ displaystyle 0.125 = cos {C}}$
8. 8 Calculate the inverse cosine. This will find the value of the unknown angle. On the calculator, the arccosine function is denoted ${ displaystyle COS ^ {- 1}}$.
   • For example, the arccosine of 0.0125 is 82.8192. So the angle S is 82.8192 °.

Method 3 of 3: Sample Problems

1. 1 Find the unknown side of the triangle. The known sides are 20 cm and 17 cm, and the angle between them is 68 °.
   • Since you are given two sides and the angle between them, you can use the cosine theorem. Write down the formula: ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$.
   • The unknown side is ${ displaystyle c}$... Plug the known values ​​into the formula: ${ displaystyle c ^ {2} = 20 ^ {2} + 17 ^ {2} -2 (20) (17) cos {68}}$.
   • Calculate ${ displaystyle c ^ {2}}$, observing the order of mathematical operations:
     ${ displaystyle c ^ {2} = 20 ^ {2} + 17 ^ {2} -2 (20) (17) cos {68}}$
     ${ displaystyle c ^ {2} = 20 ^ {2} + 17 ^ {2} -2 (20) (17) (0.3746)}$
     ${ displaystyle c ^ {2} = 20 ^ {2} + 17 ^ {2} -254.7325}$
     ${ displaystyle c ^ {2} = 400 + 289-254.7325}$
     ${ displaystyle c ^ {2} = 689-254,7325}$
     ${ displaystyle c ^ {2} = 434.2675}$
   • Take the square root of both sides of the equation. This is how you find the unknown side:
     ${ displaystyle { sqrt {c ^ {2}}} = { sqrt {434.2675}}}$
     ${ displaystyle c = 20.8391}$
     So, the unknown side is 20.8391 cm.
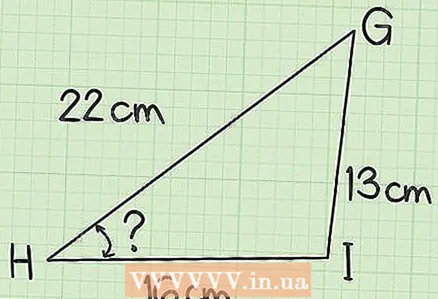2. 2 Find the angle H in triangle GHI. The two sides adjacent to the corner H are 22 and 16 cm. The side opposite to the corner H is 13 cm.
   • Since all three sides are given, the cosine theorem can be used. Write down the formula: ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$.
   • The side opposite to the unknown corner is ${ displaystyle c}$... Plug the known values ​​into the formula: ${ displaystyle 13 ^ {2} = 22 ^ {2} + 16 ^ {2} -2 (22) (16) cos {C}}$.
   • Simplify the resulting expression:
     ${ displaystyle 13 ^ {2} = 22 ^ {2} + 16 ^ {2} -704 cos {C}}$
     ${ displaystyle 13 ^ {2} = 484 + 256 - 704 cos {C}}$
     ${ displaystyle 169 = 484 + 256 - 704 cos {C}}$
     ${ displaystyle 169 = 740-704 cos {C}}$
   • Isolate the cosine:
     ${ displaystyle 169-740 = 740-740-704 cos {C}}$
     ${ displaystyle -571 = -704 cos {C}}$
     ${ displaystyle { frac {-571} {- 704}} = { frac {-704 cos {C}} {- 704}}}$
     ${ displaystyle 0.8111 = cos {C}}$
   • Find the inverse cosine. This is how you calculate the unknown angle:
     ${ displaystyle 0.8111 = cos {C}}$
     ${ displaystyle 35.7985 = COS ^ {- 1}}$.
     Thus, the angle H is 35.7985 °.
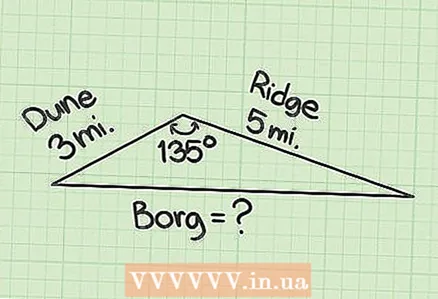3. 3 Find the length of the trail. The river, Hilly and Marsh paths form a triangle. The length of the River Trail is 3 km, the length of the Hilly Trail is 5 km; these trails intersect with each other at an angle of 135 °. The swamp trail connects the two ends of the other trails. Find the length of the Swamp Trail.
   • The trails form a triangle. You need to find the length of the unknown path, which is the side of the triangle. Since the lengths of the other two paths and the angle between them are given, the cosine theorem can be used.
   • Write down the formula: ${ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos {C}}$.
   • The unknown path (Swamp) will be denoted as ${ displaystyle c}$... Plug the known values ​​into the formula: ${ displaystyle c ^ {2} = 3 ^ {2} + 5 ^ {2} -2 (3) (5) cos {135}}$.
   • Calculate ${ displaystyle c ^ {2}}$:
     ${ displaystyle c ^ {2} = 3 ^ {2} + 5 ^ {2} -2 (3) (5) cos {135}}$
     ${ displaystyle c ^ {2} = 3 ^ {2} + 5 ^ {2} -2 (3) (5) (- 0.7071)}$
     ${ displaystyle c ^ {2} = 3 ^ {2} + 5 ^ {2} - (- 21.2132)}$
     ${ displaystyle c ^ {2} = 9 + 25 + 21.2132}$
     ${ displaystyle c ^ {2} = 55.2132}$
   • Take the square root of both sides of the equation. This is how you find the length of the unknown path:
     ${ displaystyle { sqrt {c ^ {2}}} = { sqrt {55.2132}}}$
     ${ displaystyle c = 7.4306}$
     So, the length of the Swamp Trail is 7.4306 km.

Tips

• It's easier to use the sine theorem. Therefore, first find out if it can be applied to the given problem.