Content

• Steps
• Method 1 of 4: Multiple multiples
• Method 2 of 4: Prime Factoring
• Method 3 of 4: Finding Common Divisors
• Method 4 of 4: Euclid's Algorithm
• Tips

A multiple is a number that is divisible by a given number without a remainder.The least common multiple (LCM) of a group of numbers is the smallest number that is evenly divisible by each number in the group. To find the least common multiple, you need to find the prime factors of the given numbers. The LCM can also be calculated using a number of other methods that are applicable to groups of two or more numbers.

Steps

Method 1 of 4: Multiple multiples

1. 1 Look at the given numbers. The method described here is best used when two numbers are given, each of which is less than 10. If the numbers are large, use a different method.
   • For example, find the least common multiple of 5 and 8. These are small numbers, so you can use this method.
2. 2 Write down a series of numbers that are multiples of the first number. A multiple is a number that is divisible by a given number without a remainder. Multiple numbers can be found in the multiplication table.
   • For example, numbers that are multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40.
3. 3 Write down a series of numbers that are multiples of the first number. Do this under the multiples of the first number to compare two rows of numbers.
   • For example, numbers that are multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, and 64.
4. 4 Find the smallest number that appears in both rows of multiples. You may have to write long series of multiples to find the total. The smallest number that appears in both rows of multiples is the smallest common multiple.
   • For example, the smallest number that appears in a series of multiples of 5 and 8 is 40. Therefore, 40 is the least common multiple of 5 and 8.

Method 2 of 4: Prime Factoring

1. 1 Look at the given numbers. The method described here is best used when two numbers are given, each of which is greater than 10. If the given numbers are smaller, use a different method.
   • For example, find the lowest common multiple of 20 and 84. Each of the numbers is greater than 10, so you can use this method.
2. 2 Factor out first number. That is, you need to find such prime numbers, when multiplying which you get the given number. Once you've found the prime factors, write them down as equalities.
   • For example, ${ displaystyle mathbf {2} times 10 = 20}$ and ${ displaystyle mathbf {2} times mathbf {5} = 10}$... Thus, the prime factors of 20 are 2, 2, and 5. Write them down as an expression: ${ displaystyle 20 = 2 times 2 times 5}$.
3. 3 Factor the second number. Do it in the same way as you factorized the first number, that is, find the prime numbers that, when multiplied, will give the given number.
   • For example, ${ displaystyle mathbf {2} times 42 = 84}$, ${ displaystyle mathbf {7} times 6 = 42}$ and ${ displaystyle mathbf {3} times mathbf {2} = 6}$... Thus, the prime factors of 84 are 2, 7, 3, and 2. Write them down as an expression: ${ displaystyle 84 = 2 times 7 times 3 times 2}$.
4. 4 Write down the factors common to both numbers. Write these factors down as a multiplication operation. As you write down each factor, cross it out in both expressions (expressions that describe prime factorizations).
   • For example, the common factor for both numbers is 2, so write ${ displaystyle 2 times}$ and cross out 2 in both expressions.
   • Common to both numbers is another factor of 2, so write ${ displaystyle 2 times 2}$ and cross out the second 2 in both expressions.
5. 5 Add the remaining factors to the multiplication operation. These are factors that are not crossed out in both expressions, that is, factors that are not common to both numbers.
   • For example, in the expression ${ displaystyle 20 = 2 times 2 times 5}$ both 2's (2) are crossed out because they are common factors. The factor 5 is not crossed out, so write the multiplication operation like this: ${ displaystyle 2 times 2 times 5}$
   • In the expression ${ displaystyle 84 = 2 times 7 times 3 times 2}$ also crossed out both twos (2). The factors 7 and 3 are not crossed out, so write the multiplication operation like this: ${ displaystyle 2 times 2 times 5 times 7 times 3}$.
6. 6 Calculate the least common multiple. To do this, multiply the numbers in the recorded multiplication operation.
   • For example, ${ displaystyle 2 times 2 times 5 times 7 times 3 = 420}$... So the least common multiple of 20 and 84 is 420.

Method 3 of 4: Finding Common Divisors

1. 1 Draw the grid as for a tic-tac-toe game. Such a grid consists of two parallel lines that intersect (at right angles) with the other two parallel lines. This creates three rows and three columns (the grid is very similar to the # sign). Write the first number in the first line and second column. Write the second number in the first line and third column.
   • For example, find the least common multiple of 18 and 30. Write 18 in the first row and second column, and write 30 in the first row and third column.
2. 2 Find the divisor common to both numbers. Write it down on the first row and first column. It is better to look for prime factors, but this is not a requirement.
   • For example, 18 and 30 are even numbers, so their common divisor is 2. So write 2 in the first row and first column.
3. 3 Divide each number by the first divisor. Write each quotient under the corresponding number. The quotient is the result of dividing two numbers.
   • For example, ${ displaystyle 18 div 2 = 9}$so write 9 under 18.
   • ${ displaystyle 30 div 2 = 15}$so write 15 under 30.
4. 4 Find the divisor common to both quotients. If there is no such divisor, skip the next two steps. Otherwise, write the divisor in the second row and first column.
   • For example, 9 and 15 are divisible by 3, so write 3 in the second row and first column.
5. 5 Divide each quotient by the second factor. Write each division result under the corresponding quotient.
   • For example, ${ displaystyle 9 div 3 = 3}$so write 3 under 9.
   • ${ displaystyle 15 div 3 = 5}$so write 5 under 15.
6. 6 If necessary, supplement the grid with additional cells. Repeat the described steps until the quotients have a common divisor.
7. 7 Circle the numbers in the first column and last row of the grid. Then write down the selected numbers as a multiplication operation.
   • For example, numbers 2 and 3 are in the first column, and numbers 3 and 5 are in the last row, so write the multiplication operation like this: ${ displaystyle 2 times 3 times 3 times 5}$.
8. 8 Find the result of the multiplication of numbers. This will calculate the least common multiple of the two given numbers.
   • For example, ${ displaystyle 2 times 3 times 3 times 5 = 90}$... So the least common multiple of 18 and 30 is 90.

Method 4 of 4: Euclid's Algorithm

1. 1 Remember the terminology associated with the division operation. The dividend is the number that is being divided. The divisor is the number divided by. The quotient is the result of dividing two numbers. Remainder is the number remaining when two numbers are divided.
   • For example, in the expression ${ displaystyle 15 div 6 = 2}$ ost. 3:
     15 is a dividend
     6 is the divisor
     2 is the quotient
     3 is the remainder.
2. 2 Write down an expression that describes remainder division. Expression: ${ displaystyle { text {dividend}} = { text {divisor}} times { text {quotient}} + { text {remainder}}}$... This expression will be used to write Euclid's algorithm and find the greatest common divisor of two numbers.
   • For example, ${ displaystyle 15 = 6 times 2 + 3}$.
   • The Greatest Common Divisor (GCD) is the largest number by which all given numbers are divided.
   • In this method, you first need to find the greatest common factor and then calculate the least common multiple.
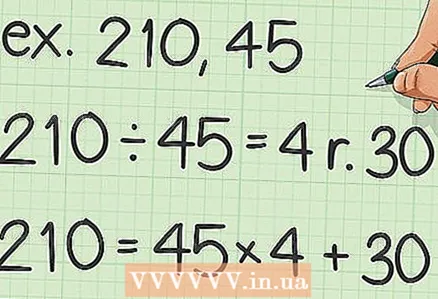3. 3 Treat the larger of the two numbers as the dividend. Consider the lesser of the two numbers as a divisor. For these numbers, write down an expression that describes remainder division.
   • For example, find the least common multiple of 210 and 45. Write this expression: ${ displaystyle 210 = 45 times 4 + 30}$.
4. 4 Turn the first divisor into a new dividend. Use the remainder as the new divisor. For these numbers, write down an expression that describes remainder division.
   • For example, ${ displaystyle 45 = 30 times 2 + 15}$.
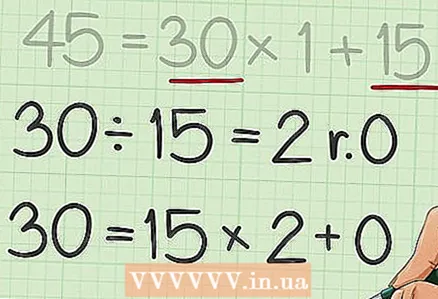5. 5 Repeat the described steps until the remainder is equal to 0. Use the previous divisor as the new dividend and the previous remainder as the new divisor; write down the appropriate expression for these numbers.
   • For example, ${ displaystyle 30 = 15 times 2 + 0}$... Since the remainder is 0, you cannot divide further.
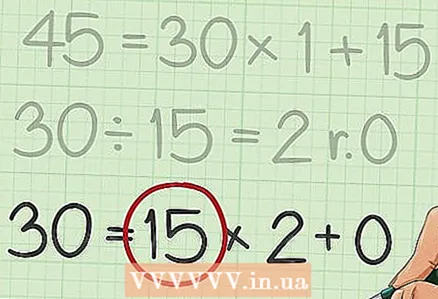6. 6 Look at the last divisor. This is the greatest common divisor of two numbers.
   • For example, the last expression was ${ displaystyle 30 = 15 times 2 + 0}$so the last divisor is 15. So 15 is the greatest common divisor of 210 and 45.
7. 7 Multiply two numbers. Then divide the product by the greatest common factor. This will calculate the least common multiple of two numbers. [[[Image: Find the Least Common Multiple of Two Numbers Step 25.webp | center]]
   • For example, ${ displaystyle 210 times 45 = 9450}$... Divide the result by GCD: ${ displaystyle { frac {9450} {15}} = 630}$... Thus, 630 is the least common multiple of 210 and 45.

Tips

• If you need to find the LCM of three or more numbers, make it easy for yourself. For example, to calculate the LCM of 16, 20, and 32, first find the least common multiple of 16 and 20 (which is 80), and then find the LCM of 80 and 32, which is 160.
• LCM has many uses. For example, to add or subtract fractions, they must have the same denominator. If fractions have different denominators, you need to transform the fractions to bring them to a common denominator. And this is easier to do if you find the smallest common denominator, which is equal to the smallest common multiple of the numbers that are in the denominators of the fractions.