Content

• Steps
• Method 1 of 3: Understand the problem statement
• Method 2 of 3: Formulate the proof
• Method 3 of 3: Write down the evidence
• Tips

Finding a mathematical proof can be a daunting task, but knowing the math and writing the proof will help you. Unfortunately, there are no quick and easy methods to learn how to solve math problems. It is necessary to study the subject properly and memorize the basic theorems and definitions that will be useful to you in proving a particular mathematical postulate. Study examples of mathematical proofs and practice yourself to help you improve your skills.

Steps

Method 1 of 3: Understand the problem statement

1. 1 Determine what you want to find. The first step is to figure out what exactly needs to be proven. Among other things, this will determine the last statement in your proof. At this stage, you should also make certain assumptions within which you will work. To better understand the problem and start solving it, find out what you need to prove and make the necessary assumptions.
2. 2 Draw a drawing. When solving mathematical problems, it is sometimes useful to depict them in the form of a picture or diagram. This is especially important in the case of geometric problems - drawing helps to visualize the condition and greatly facilitates the search for a solution.
   • When creating a picture or diagram, use the data provided in the condition. Mark the known and unknown quantities in the figure.
   • The drawing will make it easier for you to find the evidence.
3. 3 Study proofs of similar theorems. If you can't find a solution right away, find similar theorems and see how they are proved.
   • Note that you need to give reasons for each step of the proof. See how various theorems are proved on the Internet or in math textbooks.
4. 4 Ask questions. It's okay if you don't manage to find proof right away.If you are unclear about something, ask your teacher or classmates about it. Perhaps your comrades have the same questions and you can sort them out together. It is better to ask a few questions than to try and unsuccessfully find evidence over and over again.
   • Go to the teacher after lessons and find out any unclear questions.

Method 2 of 3: Formulate the proof

1. 1 Formulate a mathematical proof. A mathematical proof is a sequence of statements supported by theorems and definitions that proves a mathematical postulate. Proofs are the only way to determine if a statement is mathematically correct.
   • The ability to write down mathematical proofs testifies to a deep understanding of the problem and mastery of the necessary tools (lemmas, theorems and definitions).
   • Rigorous proof will help you take a fresh look at mathematics and get a sense of its appeal. Just try to prove a statement to get an idea of ​​mathematical methods.
2. 2 Consider your audience. Before you start recording evidence, you should think about who it is for and take into account the level of knowledge of these people. If you write down evidence for further publication in a scientific journal, it will be different from when you are doing a school assignment.
   • Knowing your target audience will allow you to write the evidence while training your readers to understand it.
3. 3 Determine the type of proof. There are several types of mathematical proofs, and the choice of a specific form depends on the target audience and the problem being solved. If you are unsure which species to choose, check with your teacher. In high school, a two-column proof is required.
   • When writing evidence in two columns, one records the original data and statements, and the second - the corresponding evidence of these statements. This form of notation is often used when solving geometric problems.
   • In a less formal way of writing evidence, grammatically correct constructions and fewer symbols are used. At higher levels, this is the notation that should be used.
4. 4 Sketch the proof in two columns. This form helps to organize thoughts and consistently solve the problem. Divide the page in half with a vertical line, and write your original data and the statements that follow from it on the left side. Write down the corresponding definitions and theorems on the right side of each statement.
   • For example:
   • corners A and B are adjacent - given;
   • angle ABC is flattened - defines a flattened corner;
   • the angle ABC is 180 ° - defining a straight line;
   • angle A + angle B = angle ABC - the rule for adding angles;
   • angle A + angle B = 180 ° - substitution;
   • angle A is complementary to angle B - defining additional angles;
   • Q.E.D.
5. 5 Write down the two-column proof as an informal proof. Use a two-column record as a basis and write the proof in a shorter form with fewer symbols and abbreviations.
   • For example: suppose corners A and B are adjacent. According to the hypothesis, these angles complement each other. When adjacent, angle A and angle B form a straight line. If the sides of the corner form a straight line, the angle is 180 °. Add angles A and B to create a straight line ABC. Thus, the sum of the angles A and B is 180 °, that is, these angles are complementary. Q.E.D.

Method 3 of 3: Write down the evidence

1. 1 Learn the language of evidence. Standard statements and phrases are used to write mathematical proofs. You need to learn these phrases and know how to use them.
   • The phrase “If A, then B” means that if statement A is true, then statement B must also be true.
   • “A if and only if B” means that statements A and B are either true or false at the same time. This construction is equivalent to two simultaneous statements: “If A, then B” and “If A fails, then B does not hold”.
   • “A only if B” is equivalent to “If B, then A”, so this construction is not common. Nevertheless, it is necessary to remember about it.
   • When recording evidence, try to use “we” instead of the personal pronoun “I”.
2. 2 Write down all the original data. When compiling a proof, the first thing to do is to define and write out everything that is given in the problem. In this case, you will have before your eyes all the initial data, on the basis of which it is necessary to obtain a decision. Read the problem statement carefully and write down everything that is given in it.
   • For example: prove that two adjacent angles (angle A and angle B) complement each other.
   • Given: adjacent corners A and B.
   • Prove: angle A is complementary to angle B.
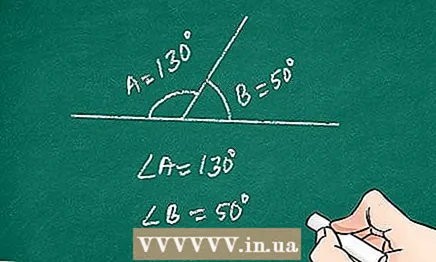3. 3 Define all the variables. In addition to recording the original data, it is also useful to write out the rest of the variables. To make it easier for the reader, write down the variables at the very beginning of the proof. If no variables are defined, the reader may get confused and not understand your proof.
   • Do not use previously undefined variables during the proof.
   • For example: in the problem considered above, the variables are the values ​​of the angles A and B.
4. 4 Try to find the proof in reverse order. Many problems are easier to solve in reverse order. Start with what you need to prove and think about how you can connect the conclusions to the initial condition.
   • Reread the starting and ending steps and see if they are similar to each other. When doing this, use the initial conditions, definitions, and similar proofs from other problems.
   • Ask yourself questions and move forward. To prove individual statements, ask yourself, "Why is this the case?" - and: "Could it be wrong?"
   • Remember to write down the individual steps sequentially until you get the final result.
   • For example: if angles A and B are complementary, their sum should be 180 °. According to the definition of adjacent angles, angles A and B form a straight line ABC. Since the line forms an angle of 180 °, angles A and B add up to 180 °.
5. 5 Arrange the individual steps of the proof so that it is consistent and logical. Start at the beginning and work your way up to a provable thesis. While it is sometimes helpful to start looking at the end of the evidence, it is important to follow the correct order when writing it. Separate theses should follow one after another so that the proof is logical and does not raise doubts.
   • First, consider the assumptions made.
   • Confirm the statements made with simple and straightforward steps so that the reader has no doubts about their correctness.
   • Sometimes you have to rewrite the proof more than once. Continue grouping statements and their evidence until you arrive at the most logical structure.
   • For example: let's start from the beginning.
     • Angles A and B are adjacent.
     • The sides of corner ABC form a straight line.
     • The ABC angle is 180 °.
     • Angle A + Angle B = Angle ABC.
     • Angle A + Angle B = Angle 180 °.
     • Angle A is complementary to angle B.
6. 6 Do not use arrows and abbreviations in the proof. Various abbreviations and symbols can be used in the draft, but do not include them in the final draft as this may confuse readers. Use words like “therefore” and “then” instead.
   • As exceptions, understandable abbreviations are allowed, for example, “ie. e. " (that is), however use them appropriately.
7. 7 Support each thesis with a theorem, law, or definition. The proof must be flawless. You cannot make unsubstantiated statements. See how proofs are built for problems similar to yours.
   • Try applying the evidence you found to cases where it shouldn't be true and see if it is. If the proof is valid in such cases, check where you went wrong.
   • Proofs of geometric problems are often written in two columns. Assertions are written on the right, and their proofs are given on the left. At the same time, in publications, mathematical proofs are drawn up in the form of paragraphs with the appropriate grammar.
8. 8 End the proofs with the phrase “as required to prove”. At the end of the proof, there must be a provable thesis. After it, you should write “what was required to prove” (abbreviated as “h. Etc.” or a symbol in the form of a filled square) - this means that the proof is complete.
   • In Latin, the phrase “what was required to prove” corresponds to the abbreviation Q.E.D. (quod erat demonstrandum, that is, “what was required to be shown”).
   • If you are in doubt about the correctness of the proof, just write a few phrases about what conclusion you came to and why it is important.

Tips

• All information provided in the evidence must serve the achievement of the stated goal. Don't include anything you can do without in your proof.