Content

• Steps
• Advice

Variance measures the dispersion of the data set. It is very useful in building statistical models: low variance can be an indication that you are describing random error or noise instead of the underlying relationship in the data. With this article, wikiHow teaches you how to calculate variance.

Steps

Method 1 of 2: Calculate the variance of a sample

1. 

   Write your sample data set. In most cases, statisticians only have information about a sample, or subset of the population they are studying. For example, instead of doing a general analysis of "the cost of all cars in Germany", a statistician might find the cost of a random sample of a few thousand cars. The statistician can use this sample to get a good estimate of the cost of cars in Germany. However, it is more likely that it will not exactly match the actual numbers.
   • For example: When analyzing the number of muffins sold per day at a coffee shop, you took a random six-day sample and got the following results: 38, 37, 36, 28, 18, 14, 12, 11, 10.7, 9.9. This is a sample, not a population, because you don't have data for every day the store is open.
   • If every Data points in the master, please go to the method below.

2. 

   
   
   Write down the sample variance formula. The variance of a data set indicates the degree of dispersion of the data points. The closer the variance is to zero, the closer the data points are grouped. When working with sample data sets, use the following formula to calculate variance:
   • = /_{(n - 1)}
   • is the variance. Variance is always calculated in squared units.
   • represents a value in your data set.
   • ∑, meaning "sum", tells you to calculate the following parameters for each value, and then add them together.
   • x̅ is the mean of the sample.
   • n is the number of data points.

3. 

   
   
   Calculate the mean of the sample. The symbol x̅ or "x-horizontal" is used to indicate the mean of the sample. Calculate as you would any average: add up all the data points and divide it by the number of points.
   • For example: First, add up your data points: 17 + 15 + 23 + 7 + 9 + 13 = 84
     Next, divide the result by the number of data points, in this case six: 84 ÷ 6 = 14.
     Sample mean = x̅ = 14.
   • You can think of the mean as the "center point" of the data. If the data is centered around the mean, variance is low. If they are dispersed far from the mean, variance is high.

4. 

   
   
   Subtract the mean from each data point. Now is the time to calculate - x̅, where each point in your data set is. Each result will indicate deviation from the mean of each corresponding point, or to put it simply, the distance from it to the mean.
   • For example:
     - x̅ = 17 - 14 = 3
     - x̅ = 15 - 14 = 1
     - x̅ = 23 - 14 = 9
     - x̅ = 7 - 14 = -7
     - x̅ = 9 - 14 = -5
     - x̅ = 13 - 14 = -1
   • It is very easy to check your calculations, because the results must sum to zero. This is because by the mean of the mean, the negative results (the distance from the mean to small numbers). positive results (distance from mean to larger numbers) are completely eliminated.

5. 

   Square all results. As noted above, the current deviation list (- x̅) has a sum of zero. That means the "mean deviation" will also always be zero and nothing can be said about the dispersion of the data. To solve this problem, we find the square of each deviation. Thanks to that, all are positive numbers, negative values ​​and positive values ​​no longer cancel each other and give the sum zero.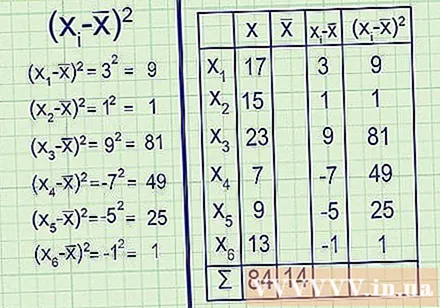
   • For example:
     (- x̅)
     - x̅)
     9 = 81
     (-7) = 49
     (-5) = 25
     (-1) = 1
   • You now have (- x̅) for each data point in the sample.

6. 

   Find the sum of the squared values. Now is the time to calculate the entire numerator of the formula: ∑. The large cyclo, ∑, requires that you add the following element value for each value. You have calculated (- x̅) for each value in the sample, so all you have to do is just add the results together.
   • For example: 9 + 1 + 81 + 49 + 25 + 1 = 166.

7. 

   Divide by n - 1, where n is the number of data points. Long ago, when calculating sample variance, statisticians only divided by n. That division will give you the mean of the squared deviation, which exactly matches the variance of that sample. However, keep in mind that the sample is only an estimate of a larger population. If you take another random sample and do the same calculation, you will get a different result. As it turns out, dividing by n -1 instead of n gives you a better estimate of the variance of a larger population - which you really care about. This correction is so common that it is now the accepted definition of sample variance.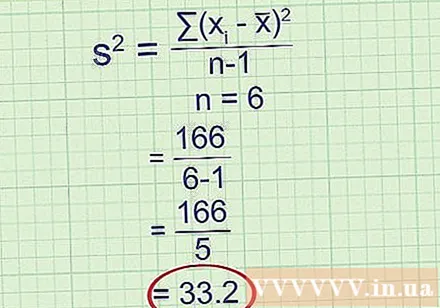
   • For example: There are six data points in the sample, so n = 6.
     Sample variance = 33,2

8. 

   Understand variance and standard deviation. Note that, since there are powers in the formula, variance is measured in the square of the units of the original data. This is visually confusing. Instead, often the standard deviation is quite useful. But there is no point in wasting any effort, as the standard deviation is determined by the square root of the variance. That's why the sample variance is written as, and the standard deviation of a sample is.
   • For example, the standard deviation of the above sample = s = √33.2 = 5.76.
   advertisement

Method 2 of 2: Calculate variance of a population

1. 

   Starting with the master data set. The term "population" is used to refer to all relevant observations. For example, if you are researching the age of Hanoi residents, your overall population will include the ages of all individuals living in Hanoi. Usually you would create a spreadsheet for a large data set like this, but here's a smaller example data set:
   • For example: In the room of an aquarium, there are exactly six aquariums. These six tanks contain the following numbers of fish:
     
     
     
     
     
     

2. 

   Write down the formula for overall variance. Since a population contains all the data we need, this formula gives us the exact variance of the population. To distinguish it from the sample variance (which is only an estimate), statisticians use other variables:
   • σ = /_n
   • σ = sample variance. This is the normally squared sausage. Variance is measured in squared units.
   • represents an element in your data set.
   • The element in ∑ is calculated for each value, and then added up.
   • μ is the overall mean.
   • n is the number of data points in the population.

3. 

   Find the mean of the population. When analyzing a population, the symbol μ ("mu") represents the arithmetic mean. To find the mean, add up all the data points, then divide by the number of points.
   • You can think of mean as "average", but be careful, because the word has many mathematical definitions.
   • For example: mean value = μ = = 10,5

4. 

   Subtract the mean from each data point. Data points closer to the mean have a difference closer to zero. Repeat the subtraction problem for all the data points, and you will probably begin to feel the dispersion of the data.
   • For example:
     - μ = 5 – 10,5 = -5,5
     - μ = 5 – 10,5 = -5,5
     - μ = 8 – 10,5 = -2,5
     - μ = 12 - 10., = 1,5
     - μ = 15 – 10,5 = 4,5
     - μ = 18 – 10,5 = 7,5

5. 

   Square each sign. At this point, some results obtained from the previous step will be negative and some will be positive.If you visualize the data on an isomorphic line, these two items represent the numbers to the left and right of the mean. This would be of no use in calculating variance, as these two groups would cancel each other out. Instead, square them all so they are all positive.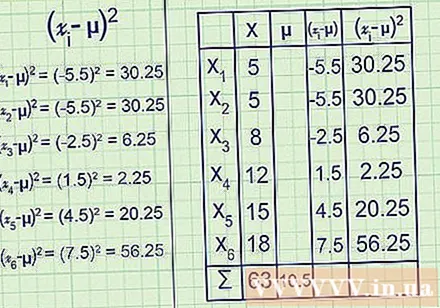
   • For example:
     (- μ) for each value of i runs from 1 to 6:
     (-5,5) = 30,25
     (-5,5) = 30,25
     (-2,5) = 6,25
     (1,5) = 2,25
     (4,5) = 20,25
     (7,5) = 56,25

6. 

   Find the average of your results. You now have a value for each data point, related (not directly) to how far away that data point is from the mean. Average by adding them together and dividing by the number of values ​​you have.
   • For example:
     Overall variance = 24,25

7. 

   Contact recipe. If you are not sure how this fits the formula outlined at the beginning of the method, write the whole problem down by hand, and don't abbreviate: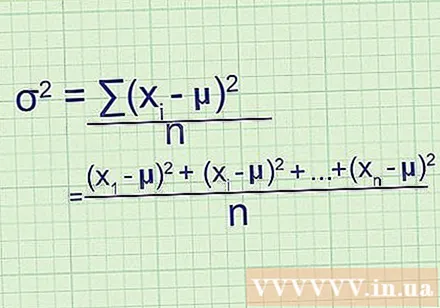
   • After finding the difference from the mean and squaring, you get (- μ), (- μ), and so on until (- μ), where is the last data point. in the data set.
   • To find the average of these values, add them together and divide by n: ((- μ) + (- μ) + ... + (- μ)) / n
   • After rewriting the numerator with sigmoid notation, you have /_n, formula variance.
   advertisement

Advice

• Because the variance is difficult to interpret, this value is often calculated as the starting point for finding the standard deviation.
• Using "n-1" instead of "n" in the denominator is a technique called Bessel correction. The sample is only an estimate of a complete population, and the mean of the sample has a certain bias to match that estimate. This correction eliminates the above bias. It concerns the fact that once n - 1 data points have been enumerated, the last th point n was a constant, because only certain values ​​were used to calculate the mean of the sample (x̅) in the variance formula.