Analyze quadratic equations into factors - tips

Video: How To Solve Quadratic Equations By Factoring - Quick & Simple!

Content

Steps
Advice
What you need

In math, factor analysis is to find numbers or expressions with the product of a given number or equation. Factor analysis is a useful skill to learn for solving basic algebraic problems: the ability to factorize well is almost critical when it comes to working. with algebraic equations or other polynomial forms. Factor analysis can be used to reduce algebraic expressions, making the problem simpler. Thanks to it, you can even eliminate certain possible answers much faster than solving by hand.

Steps

Method 1 of 3: Analyze numbers and basic algebraic expressions into factors

Understand the definition of factor analysis when applying to single numbers. Though conceptually simple, in practice, applying complex equations can be quite challenging. Therefore, the easiest factor-analysis conceptual approach is to start from single numbers and then move on to simple equations before proceeding with more advanced applications. Factor for a given number are numbers with the product of the same number. For example, 1, 12, 2, 6, 3 and 4 are factors of 12 because 1 × 12, 2 × 6, and 3 × 4 are all equal to 12.
- In other words, the factors of a given number are numbers is divided by that number.
- Can you find the full factor of 60? The number 60 is used for many different purposes (minutes in an hour, seconds in a minute, etc.) because it is divisible by many numbers.
  - The number 60 has the following factors: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
Understand that expressions containing variables can also be factorized. As well as independent numbers, variables with arithmetic coefficients can also be factorized. To do this, we just need to find the factors of the coefficient of the variable. Knowing how to factorize analysis is very useful in simply transforming algebraic equations that contain variables.
- For example 12x can be rewritten to be results of 12 and x. It is possible to write 12x as 3 (4x), 2 (6x), etc., and use whatever factor best suits the intended use of 12.
  - You can even go as far as 12x analysis many times. In other words, there is no need to stop at 3 (4x) or 2 (6x) - we can analyze 4x and 6x to get 3 (2 (2x) 2 (3 (2x)) respectively. This formula is equivalent.
Apply associative properties of multiplication to factorize algebraic equations. Using your knowledge of analyzing both independent numbers and coefficients into factors, you can simplify simple algebraic equations by finding common factors of the numbers and variables included in the equation. Often, for the equation to be as simple as possible, we will try to find the greatest common divisor. This simple transformation is possible thanks to the associative nature of multiplication - for every number a, b, and c, we have: a (b + c) = ab + ac.
- Let's consider the following example problem. To factor the algebraic equation 12x + 6 into a factor, first, we find the greatest common divisor of 12x and 6. 6 is the largest number that both 12x and 6 are divisible by, so we can simply transform reduce the equation to 6 (2x + 1).
- The same process applies to equations that bear negative signs and fractions. For example x / 2 + 4 can be simply converted to 1/2 (x + 8), and -7x + -21 can be decomposed to -7 (x + 3).
advertisement

Method 2 of 3: Analysis of quadratic equations into factors

Make sure that the equation is in quadratic form (ax + bx + c = 0). The quadratic equation has the form ax + bx + c = 0, where a, b, and c are constants and a is nonzero (note that a may equals 1 or -1). If the one-variable (x) equation contains one or more terms that contain the square of x, you can usually convert the basic algebraic operator on one side of the equal sign to 0 and let ax, and so on. on the other side.
- For example, the algebraic equation 5x + 7x - 9 = 4x + x - 18 can be reduced to x + 6x + 9 = 0, which is a quadratic form.
- Equations where x has a higher exponent, such as x, x, and so on. cannot be quadratic. They are quadratic, quadratic, ... unless the equation can be reduced by eliminating terms that contain the powers of 3 or more of x.
With quadratic equations, when a = 1, we decompose to (x + d) (x + e), where d × e = c and d + e = b. If the quadratic equation is in the form x + bx + c = 0 (in other words, if the coefficient of x = 1), there is a possibility (but not sure) that we can use a relatively fast calculation. it is simple to factor this equation. Find two numbers equal to c and the sum equals b. Once you have found d and e, replace them with the following expression: (x + d) (x + e). When multiplied together, these two elements give us the quadratic equation above - in other words, they are factors of the equation.
- Take for example the quadratic equation x + 5x + 6 = 0. 3 and 2 have a product of 6 and at the same time, have a total of 5. Therefore, we can simply convert the equation to (x + 3) ( x + 2).
- This basic quick fix will be a little bit different when the equation itself is a little different:
  - If the quadratic equation is in the form x-bx + c, your answer will be of the form: (x - _) (x - _).
  - If it's in the form x + bx + c, your answer will be: (x + _) (x + _).
  - If it's in x-bx-c, your response will be in the form (x + _) (x - _).
- Note: in spaces can be fractions or decimals. For example, the equation x + (21/2) x + 5 = 0 decomposes to (x + 10) (x + 1/2).
If possible, perform factor analysis by testing. Believe it or not, with the uncomplicated quadratic equation, one of the accepted methods of factorization is simply to look at the problem, and then weigh all the possible answers until a result is found. correct answer. It is also known as the test method.If the equation has the form ax + bx + c and a> 1, your factor analysis will have the form (dx +/- _) (ex +/- _), where d and e are constants the other is not equal to a. d or e (or both) may equals 1, although it won't necessarily be. If both equals 1, you would have basically used the quick work shown above.
- Consider the following example problem. At first glance, 3x - 8x + 4 looks quite intimidating. However, once you realize that 3 has only two factors (3 and 1), the problem becomes easier because we know the answer must be of the form (3x +/- _) (x +/- _). In this case, substituting -2 in both spaces gives the correct answer. -2 × 3x = -6x and -2 × x = -2x. -6x and -2x total equal to -8x. -2 × -2 = 4, therefore, it can be seen that the elements parsed in parentheses give us the initial equation.
Solve the problem by completing the square. In some cases, quadratic equations can be multiplied quickly and easily using a special algebraic identity. Any quadratic equation of the form x + 2xh + h = (x + h). Therefore, if in the equation, b is twice the square root of c, the equation can be decomposed into (x + (sqrt (c))).
- The equation x + 6x + 9 would work for this form, for example. 3 equals 9 and 3 × 2 equals 6. So we know that the factorization form of this equation is (x + 3) (x + 3), or (x + 3).
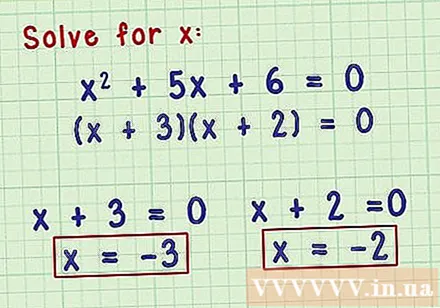
Solve quadratic equations with factors. Either way, once the quadratic expression has been factorized, you can find a possible answer to the value of x by giving each factor zero and solving it. Since you are looking for the value of x such that the equation is zero, any x that causes a factor to be zero will be a possible solution to that equation.
- Go back to the equation x + 5x + 6 = 0. This is decomposed to (x + 3) (x + 2) = 0. When one factor is zero, the whole equation becomes zero. Possible solutions of x are the numbers that make (x + 3) and (x + 2) equal to 0, -3 and -2, respectively.
Check your answers - some may be exotic! When you find possible solutions of x, replace them with the original equation to determine if they are correct or not. Sometimes, the answer finds it no problem causes the original equation to be zero when replaced. We call these solutions Exotic and eliminate them.
- Let's replace -2 and -3 for x + 5x + 6 = 0. First, -2:
  - (-2) + 5(-2) + 6 = 0
  - 4 + -10 + 6 = 0
  - 0 = 0. Yes, so -2 is a valid solution of the equation.
- Now let's try with -3:
  - (-3) + 5(-3) + 6 = 0
  - 9 + -15 + 6 = 0
  - 0 = 0. This is also true and therefore, -3 is also a valid solution of the equation.
advertisement

Method 3 of 3: Analyze other types of equations into factors

If the equation is in the a-b form, decompose it to (a + b) (a-b). The two-variable equation is analyzed differently than the fundamental quadratic equation. Any a-b equation in which a and b are nonzero will be decomposed into (a + b) (a-b).
- For example, the equation 9x - 4y = (3x + 2y) (3x - 2y).
If the equation is in the form a + 2ab + b, decompose it to (a + b). Note that if the trinomial is in the form a-2ab + b, the factorization form will differ slightly: (a-b).
- Equations 4x + 8xy + 4y can be rewritten as 4x + (2 × 2 × 2) xy + 4y. Now we see that it is in the correct form and can confidently say that the factorization form of this equation is (2x + 2y).
If the equation is in the a-b form, decompose it to (a-b) (a + ab + b). Finally, it should be said that ternary equations and even higher order equations can be factorized. However, the analysis process will quickly become incredibly complex.
- For example, 8x - 27y decomposes to (2x - 3y) (4x + ((2x) (3y)) + 9y)
advertisement

Advice

a-b can be factorized, and a + b cannot.
Remember how to factor constants - it might help.
Pay attention to fractions in the process of factorization, handle them correctly and appropriately.
With the x + bx + (b / 2) trident, its factorization would be (x + (b / 2)) (you might come across this situation while completing the square).
Remember that a0 = 0 (property multiplied by zero).