Author:
John Pratt
Date Of Creation:
9 April 2021
Update Date:
26 June 2024

Content
A square pyramid is a three-dimensional figure with a square base and triangular sloping sides that meet at one point above the base. In the event that  Measure the length of the side of the base. Because square pyramids by definition have a square base, all sides of the base should be equal in length. So with a square pyramid you only need to know the length of one of the sides.
Measure the length of the side of the base. Because square pyramids by definition have a square base, all sides of the base should be equal in length. So with a square pyramid you only need to know the length of one of the sides.
- Suppose you have a pyramid with a square base whose sides have a length of
 Calculate the area of the ground plane. To determine the volume, you first need the area of the base. You do this by multiplying the length and width of the base. Because the base of a square pyramid is a square, all sides have the same length, and the area of the base is equal to the square of the length of one of the sides (and is thus multiplied by itself).
Calculate the area of the ground plane. To determine the volume, you first need the area of the base. You do this by multiplying the length and width of the base. Because the base of a square pyramid is a square, all sides have the same length, and the area of the base is equal to the square of the length of one of the sides (and is thus multiplied by itself). - In the example, the sides of the base of the pyramid are all 5 cm, and you calculate the area of the base as follows:
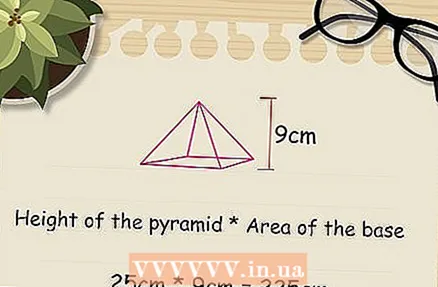 Multiply the area of the base by the height of the pyramid. Then multiply the base area by the height of the pyramid. As a reminder, height is the distance is the length of the line segment from the top of the pyramid to the base, at a right angle.
Multiply the area of the base by the height of the pyramid. Then multiply the base area by the height of the pyramid. As a reminder, height is the distance is the length of the line segment from the top of the pyramid to the base, at a right angle. - In the example we state that the pyramid has a height of 9 cm. In this case, multiply the area of the base by this value, as follows:
 Divide this answer by 3. Finally, you determine the volume of the pyramid by dividing the value you just found (by multiplying the area of the base by the height) by 3. This calculates the volume of the square pyramid.
Divide this answer by 3. Finally, you determine the volume of the pyramid by dividing the value you just found (by multiplying the area of the base by the height) by 3. This calculates the volume of the square pyramid. - In the example, divide 225 cm by 3 to answer 75 cm for the volume.
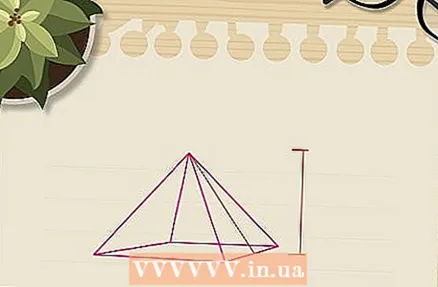 Measure the pyramid's apothem. Sometimes not the perpendicular height of the pyramid is given (or should you measure it), but the apothem. With the apothem you can use the Pythagorean Theorem to calculate the perpendicular height.
Measure the pyramid's apothem. Sometimes not the perpendicular height of the pyramid is given (or should you measure it), but the apothem. With the apothem you can use the Pythagorean Theorem to calculate the perpendicular height. - The apothem of a pyramid is the distance from the top to the center of one side of the base. Measure to the center of one side and not to one corner of the base. For this example we assume that the apothem is 13 cm and the length of one side of the base is 10 cm.
- Remember that the Pythagorean Theorem can be expressed as the equation
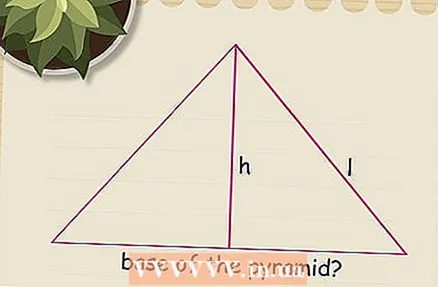
 Imagine a right triangle. To use the Pythagorean Theorem you need a right triangle. Imagine a triangle dividing the pyramid in half and perpendicular to the base of the pyramid. The pyramid's apothem, called
Imagine a right triangle. To use the Pythagorean Theorem you need a right triangle. Imagine a triangle dividing the pyramid in half and perpendicular to the base of the pyramid. The pyramid's apothem, called  Assign variables to the values. The Pythagorean Theorem uses variables a, b and c, but it is useful to replace them with variables that are meaningful to your assignment. The apothem
Assign variables to the values. The Pythagorean Theorem uses variables a, b and c, but it is useful to replace them with variables that are meaningful to your assignment. The apothem  Use the Pythagorean Theorem to calculate the perpendicular height. Use the measured values
Use the Pythagorean Theorem to calculate the perpendicular height. Use the measured values  Use the height and base to calculate the volume. After applying these calculations to the Pythagorean Theorem, you now have the information you need to calculate the volume of the pyramid. Use the formula
Use the height and base to calculate the volume. After applying these calculations to the Pythagorean Theorem, you now have the information you need to calculate the volume of the pyramid. Use the formula  Measure the height of the pyramid's legs. The height of the legs is the length of the edges of the pyramid, measured from the top to one corner of the base. As above, use the Pythagorean Theorem to calculate the perpendicular height of the pyramid.
Measure the height of the pyramid's legs. The height of the legs is the length of the edges of the pyramid, measured from the top to one corner of the base. As above, use the Pythagorean Theorem to calculate the perpendicular height of the pyramid. - In this example we assume that the height of the legs is 11 cm and the perpendicular height is 5 cm.
 Imagine a right triangle. Again, you need a right triangle to be able to use the Pythagorean Theorem. In this case, however, the unknown value is the base of the pyramid. The vertical height and the height of the legs are known. Now imagine that you cut the pyramid diagonally from one corner to the other, and then open the figure, and the resulting face looks like a triangle. The height of that triangle is the perpendicular height of the pyramid. This divides the exposed triangle into two symmetrical right triangles. The hypotenuse of each of the right triangles is the height of the legs of the pyramid. The base of each of the right triangles is half the diagonal of the base of the pyramid.
Imagine a right triangle. Again, you need a right triangle to be able to use the Pythagorean Theorem. In this case, however, the unknown value is the base of the pyramid. The vertical height and the height of the legs are known. Now imagine that you cut the pyramid diagonally from one corner to the other, and then open the figure, and the resulting face looks like a triangle. The height of that triangle is the perpendicular height of the pyramid. This divides the exposed triangle into two symmetrical right triangles. The hypotenuse of each of the right triangles is the height of the legs of the pyramid. The base of each of the right triangles is half the diagonal of the base of the pyramid.  Assign variables. Use the imaginary right triangle and assign values to the Pythagorean Theorem. You know the perpendicular height,
Assign variables. Use the imaginary right triangle and assign values to the Pythagorean Theorem. You know the perpendicular height,  Calculate the diagonal of the square base. You have to rearrange the equation around the variable
Calculate the diagonal of the square base. You have to rearrange the equation around the variable  Determine the side of the base of the diagonal. The base of the pyramid is a square. The diagonal of each square is equal to the length of one of its sides times square root 2. So you can find the side of a square by dividing the diagonal by square root 2.
Determine the side of the base of the diagonal. The base of the pyramid is a square. The diagonal of each square is equal to the length of one of its sides times square root 2. So you can find the side of a square by dividing the diagonal by square root 2. - In this pyramid example, the diagonal of the base is 7.5 inches. Therefore the side is equal to:
 Calculate the volume using the side and height. Return to the original formula to calculate the volume using the side and perpendicular height.
Calculate the volume using the side and height. Return to the original formula to calculate the volume using the side and perpendicular height.
- In this pyramid example, the diagonal of the base is 7.5 inches. Therefore the side is equal to:
- For a square pyramid, the perpendicular height, apothem and the length of the edge of the base can all be calculated with the Pythagorean Theorem.
Method 2 of 3: Determine the volume with the apothem
Tips
- In the example we state that the pyramid has a height of 9 cm. In this case, multiply the area of the base by this value, as follows:
- In the example, the sides of the base of the pyramid are all 5 cm, and you calculate the area of the base as follows: