Author:
Judy Howell
Date Of Creation:
2 July 2021
Update Date:
1 July 2024
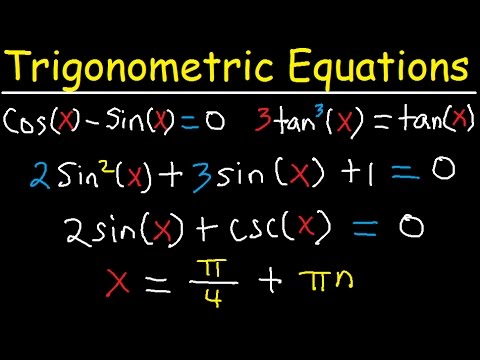
Content
A trigonometric equation is an equation with one or more trigonometric functions of the variable trigonometric curve x. Solving for x means finding the values of the trigonometric curves whose trigonometric functions cause the trigonometric equation to be true.
- Answers, or values, of the solution curves are expressed in degrees or radians. Examples:
x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 degrees; x = 37.12 degrees; x = 178.37 degrees
- Note: On the unit circle, the trigonometric functions of any curve are equal to the trigonometric functions of the corresponding angle. The unit circle defines all trigonometric functions of the variable curve x. It is also used as proof in solving basic trigonometric equations and inequalities.
- Examples of trigonometric equations:
- sin x + sin 2x = 1/2; tan x + cot x = 1.732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.
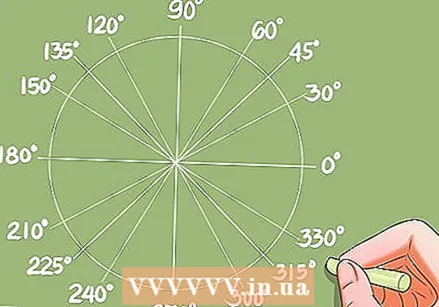
- The unit circle.
- This is a circle with Radius = 1, where O is the origin. The unit circle defines 4 main trigonometric functions of the variable curve x, which circles it counterclockwise.
- When the curve with value x varies on the unit circle, then holds:
- The horizontal axis OAx defines the trigonometric function f (x) = cos x.
- The vertical axis OBy defines the trigonometric function f (x) = sin x.
- The vertical axis AT defines the trigonometric function f (x) = tan x.
- The horizontal axis BU defines the trigonometric function f (x) = cot x.
- The unit circle is also used to solve basic trigonometric equations and standard trigonometric inequalities by considering the various positions of the curve x on the circle.
To step
 Understand the solution method.
Understand the solution method.- To solve a trigonometric equation you convert it into one or more basic trigonometric equations. Solving trigonometric equations ultimately results in solving 4 basic trigonometric equations.
 Know how to solve basic trigonometric equations.
Know how to solve basic trigonometric equations.- There are 4 basic trigonometric equations:
- sin x = a; cos x = a
- tan x = a; cot x = a
- You can solve the basic trigonometric equations by studying the various positions of the curve x on the trigonometric circle and by using a trigonometric conversion table (or calculator). To fully understand how to solve these and similar basic trigonometric equations, read the following book: "Trigonometry: Solving Trigonometric Equations and inequalities" (Amazon E-book 2010).
- Example 1. Solve for sin x = 0.866. The conversion table (or calculator) gives the answer: x = Pi / 3. The trigonometric circle gives another curve (2Pi / 3) with the same value for the sine (0.866). The trigonometric circle also provides an infinity of answers called extended answers.
- x1 = Pi / 3 + 2k.Pi, and x2 = 2Pi / 3. (Replies within a period (0, 2Pi))
- x1 = Pi / 3 + 2k Pi, and x2 = 2Pi / 3 + 2k Pi. (Detailed answers).
- Example 2. Solve: cos x = -1/2. Calculators give x = 2 Pi / 3. The trigonometric circle also gives x = -2Pi / 3.
- x1 = 2Pi / 3 + 2k.Pi, and x2 = - 2Pi / 3. (Answers for period (0, 2Pi))
- x1 = 2Pi / 3 + 2k Pi, and x2 = -2Pi / 3 + 2k.Pi. (Extended Answers)
- Example 3. Solve: tan (x - Pi / 4) = 0.
- x = Pi / 4; (Answer)
- x = Pi / 4 + k Pi; (Extended answer)
- Example 4. Solve: cot 2x = 1.732. Calculators and the trigonometric circle give:
- x = Pi / 12; (Answer)
- x = Pi / 12 + k Pi; (Extended Answers)
 Learn the transformations used in solving trigonometric equations.
Learn the transformations used in solving trigonometric equations.- To convert a given trigonometric equation to standard trigonometric equations, use standard algebraic conversions (factorization, common factor, polynomials ...), definitions and properties of trigonometric functions and trigonometric identities. There are about 31, 14 of which are trigonometric identities, from 19 to 31, also called transformation identities, because they are used in the conversion of trigonometric equations. See the above book.
- Example 5: The trigonometric equation: sin x + sin 2x + sin 3x = 0 can be converted into a product of basic trigonometric equations using trigonometric identities: 4cos x * sin (3x / 2) * cos (x / 2) = 0. The basic trigonometric equations to solve are: cos x = 0; sin (3x / 2) = 0; and cos (x / 2) = 0.
 Find the curves for which the trigonometric functions are known.
Find the curves for which the trigonometric functions are known.- Before you can learn how to solve trigonometric equations, you need to know how to quickly find the curves for which the trigonometric functions are known. Conversion values of curves (or angles) can be determined with trigonometric tables or the calculator.
- Example: Solve for cos x = 0.732. The calculator gives the solution x = 42.95 degrees. The unit circle gives other curves with the same value for the cosine.
 Draw the arc of the answer on the unit circle.
Draw the arc of the answer on the unit circle.- You can create a graph to illustrate the solution on the unit circle. The end points of these curves are regular polygons on the trigonometric circle. Some examples:
- The endpoints of the curve x = Pi / 3 + k. Pi / 2 is a square on the on the unit circle.
- The curves of x = Pi / 4 + k.Pi / 3 are represented by the coordinates of a hexagon on the unit circle.
 Learn how to solve trigonometric equations.
Learn how to solve trigonometric equations.- If the given trigonometric equation contains only one trigonometric function, solve it as a standard trigonometric equation. If the given equation contains two or more trigonometric functions, there are 2 solution methods, depending on the options for converting the equation.
- A. Method 1.
- Convert the trigonometric equation to a product of the form: f (x) .g (x) = 0 or f (x) .g (x) .h (x) = 0, where f (x), g (x ) and h (x) are basic trigonometric equations.
- Example 6. Solve: 2cos x + sin 2x = 0. (0 x 2Pi)
- Solution. Replace sin 2x in the equation using the identity: sin 2x = 2 * sin x * cos x.
- cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Then solve 2 standard trigonometric functions: cos x = 0, and (sin x + 1) = 0.
- Example 7. Solve: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
- Solution: Convert this into a product, using the trigonometric identities: cos 2x (2cos x + 1) = 0. Now solve the 2 basic trigonometric equations: cos 2x = 0, and (2cos x + 1) = 0.
- Example 8. Solve: sin x - sin 3x = cos 2x. (0 x 2Pi)
- Solution: Convert this into a product, using the trigonometric identities: -cos 2x * (2sin x + 1) = 0. Now solve the 2 basic trigonometric equations: cos 2x = 0, and (2sin x + 1) = 0.
- B. Approach 2.
- Converts the trig equation to a trig equation with only one unique trig function as a variable. There are some tips on how to choose a suitable variable. Common variables are: sin x = t; cos x = t; cos 2x = t, tan x = t and tan (x / 2) = t.
- Example 9. Solve: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
- Solution. In the equation, replace (cos ^ 2x) with (1 - sin ^ 2x), and simplify the equation:
- 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Now use sin x = t. The equation becomes: 5t ^ 2 - 4t - 9 = 0. This is a quadratic equation with 2 roots: t1 = -1 and t2 = 9/5. We can reject the second t2, because> 1. Now solve for: t = sin = -1 -> x = 3Pi / 2.
- Example 10. Solve: tan x + 2 tan ^ 2 x = cot x + 2.
- Solution. Use tan x = t. Convert the given equation into an equation with t as a variable: (2t + 1) (t ^ 2 - 1) = 0. Solve for t from this product, then solve for the standard trigonometric equation tan x = t for x .
- If the given trigonometric equation contains only one trigonometric function, solve it as a standard trigonometric equation. If the given equation contains two or more trigonometric functions, there are 2 solution methods, depending on the options for converting the equation.
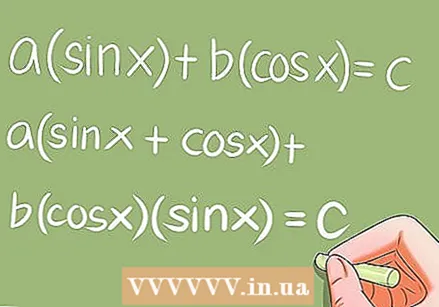 Solve special trigonometric equations.
Solve special trigonometric equations.- There are a few special trigonometric equations that require some specific conversions. Examples:
- a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
- a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
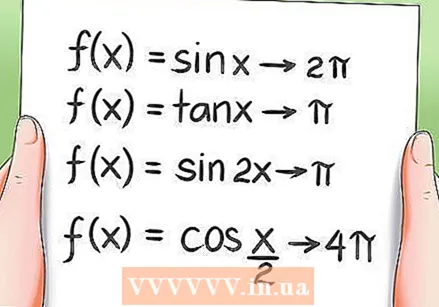 Learn the periodic properties of trigonometric functions.
Learn the periodic properties of trigonometric functions.- All trigonometric functions are periodic, which means that they return to the same value after a rotation over a period. Examples:
- The function f (x) = sin x has 2Pi as a period.
- The function f (x) = tan x has Pi as a period.
- The function f (x) = sin 2x has Pi as a period.
- The function f (x) = cos (x / 2) has 4Pi as period.
- If the period is specified in the exercises / test, then you just need to find the curve (s) x within this period.
- NOTE: Solving trigonometric equations is tricky and often leads to errors and mistakes. Therefore, answers should be carefully checked. After solving, you can check the answers using a graphing calculator, for a direct representation of the given trigonometric equation R (x) = 0. The answers (as square root) are given in decimal places. As an example, Pi has a value of 3.14
- All trigonometric functions are periodic, which means that they return to the same value after a rotation over a period. Examples: