Content

• To step
• Method 1 of 6: Subtract large integers by borrowing
• Method 2 of 6: Subtract small integers
• Method 3 of 6: Subtracting decimals
• Method 4 of 6: Subtracting fractions
• Method 5 of 6: Subtract a fraction from an integer
• Method 6 of 6: Subtracting variables
• Tips
• Warnings

Subtraction sums are those sums where you subtract two numbers from each other. It's quite simple if you want to subtract whole numbers, but it gets a bit more complicated when you're working with fractions or decimals. Once you've mastered subtraction you can move on to the more complicated math concepts and adding, multiplying and dividing numbers will be much easier.

To step

Method 1 of 6: Subtract large integers by borrowing

1. Write down the larger number. Suppose you are working with the sum 32 - 17. Write down 32 first.
2. Write the smaller number directly below it. Line up the tens and units neatly, so that the 3 in "32" is directly above the 1 in "17", and the 2 in "32" is directly above the "7" in 17.
3. Subtract the bottom number from the top one. This can get a bit tricky if the bottom number is greater than the top one. In this case, 7 is greater than 2. Here's what to do:
   • You will have to "borrow" the 3 in "32" to make the 2 a 12.
   • Cross the 3 of "32" and make it a 2, then make the unit 2 a 12.
   • Now you have 12 - 7 = 5. Write a 5 under the column with the units.
4. Subtract the tens in the bottom number from the tens in the top number. Remember that the 3 of 32 has become a 2. Now subtract the 1 in 17 from the 2 above, so 2-1 = 1. Write 1 under the tens column. You should now have the answer 15, so 32 - 17 = 15.
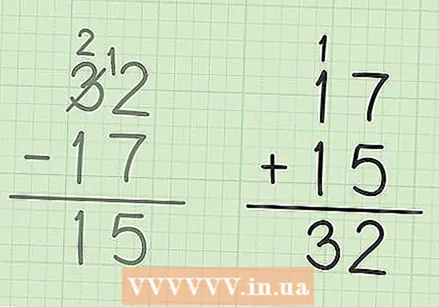5. Check your work. If you want to make sure you've done the calculation correctly, all you have to do is add the answer to the smallest number to get the largest number back. So just to check: 15 + 17 = 32, so you did a good job. Excellent!

Method 2 of 6: Subtract small integers

1. Determine which number is greater. An exercise such as 15 - 9 requires a different approach than 2 - 30.
   • In the sum 15 - 9, the first number, 15, is the largest.
   • In the sum 2 - 30, the second number, 30, is the largest.
2. Determine whether your answer should be positive or negative. If the first number is the largest, the answer becomes positive. If the second number is the largest, the answer will be negative.
   • So in the first sum, 15 - 9, the answer becomes positive, because 15 is greater than 9.
   • So in the second sum, 2 - 30, the answer becomes negative, because 2 is less than 30.
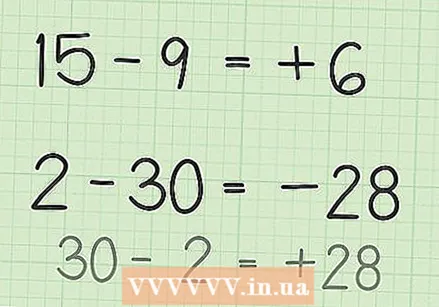3. Find the difference between the two numbers. To subtract two numbers, calculate the difference between them.
   • For problem 15 - 9, take 15 coins. Remove 9 and count how many are left (6). So, 15 - 9 = 6. Or use a number line and draw the numbers 1 through 15 along the line, after which you cross out 9 from 15 down to get to 6.
   • With the sum 2 - 30 it is easier to turn the numbers around and make the answer negative. So, 30 - 2 = 28, so 2 - 30 is -28.

Method 3 of 6: Subtracting decimals

1. Write the larger number above the smaller number so that the decimal places are aligned. Suppose you have the following problem: 10.5 - 8.3. Write the 10.5 above 8.3 so that the commas are one above the other.
   • If you have a problem where one number has more decimal places than the other number, fill the empty space with zeros. For example, if you have the problem 5.32 - 4.2, you can rewrite this as 5.32 = 4.20. This does not change the value of a number, but it does make it easier for both numbers to be subtracted from each other.
2. Subtract the tenths. Subtraction of these numbers is the same as with integers, except that you have to pay attention to the comma, aligned and included in the answer. In this case, you have to subtract 3 from 5.5 - 3 = 2, so you write a 2 under 3 in 8.3.
   • Do not forget to include the decimal point (the comma) in the answer. This now looks like this:, 2.
3. Now subtract the units from each other. Now you subtract 8 from 0. Borrow a dozen of the 1 (next to the 0) to make it 10, and now subtract 8 from 10. You can also immediately calculate the sum 10 - 8 = 2, without the intermediate step of the borrowing, because the bottom number does not have a decade. Write the answer below 8.
4. So the final answer becomes 2.2.
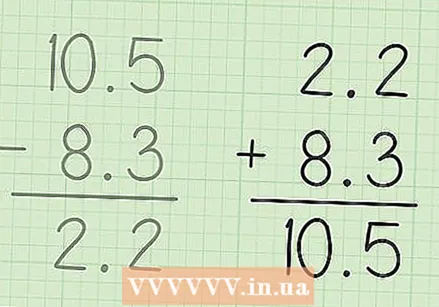5. Check your work. If you want to make sure you've done the calculation correctly, all you have to do is add the answer to the smallest number to get the largest number back. 2.2 + 8.3 = 10.5 so you're all set.

Method 4 of 6: Subtracting fractions

1. Put the numerators and denominators together. Suppose you are working with the problem 13/10 - 3/5. Write this problem so that both numerators, 13 and 3, and both denominators, 10 and 5, are next to each other, separated by a minus sign. This gives you a better overview of the problem and makes it easier to find a solution.
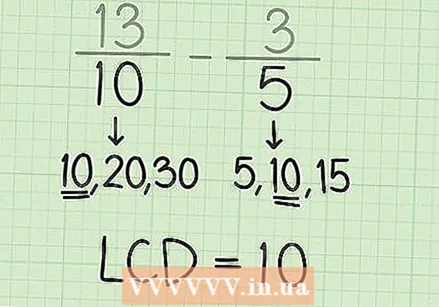2. Find the least common multiple. This is the smallest multiple of two numbers. The LCM of 10 and 5 in this example is 10.
   • Note that the LCM of two numbers is not always either number. For example, for 3 and 2, the LCM is 6, because there is no number smaller than 6 which is a multiple for each of the numbers.
3. Rewrite fractions with the same denominators. The fraction 13/10 stays unchanged because the denominator hasn't changed, but the fraction 3/5 becomes equal to 6/10 because the denominator goes into the common multiple of 10 twice. Now you have made both fractions the same name. 3/5 is equal to 6/10, except that it is no longer a problem to subtract both fractions from each other.
   • The new entry will therefore be: 13/10 - 6/10.
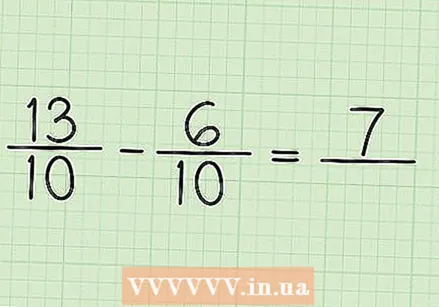4. Subtract both counters. So 13 - 6 = 7. You don't subtract the denominators.
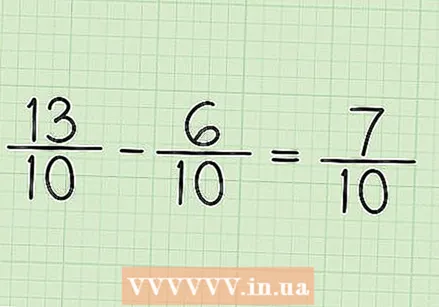5. Place the new numerator above the new denominator (the previously calculated LCM) for the final answer. The new numerator is 7 and the denominator of both fractions is 10. So the final answer is 7/10.
6. Check your work. If you want to make sure you've done the calculation correctly, all you have to do is add the answer to the smallest number to get the largest number back. So as a check: 7/10 + 6/10 = 13/10. You are now all set.

Method 5 of 6: Subtract a fraction from an integer

1. Write down the statement. Suppose we have the following problem: 5 - 3/4. Make a note of this.
2. Make the whole number into a fraction with the same denominator as the given fraction. Make a fraction of the 5 with denominator 4. First, consider that 5 is equal to the fraction 5/1. Then multiply both the numerator and denominator of the new fraction by 4 to get two fractions with the same denominator. This keeps the value of the fraction the same, but with different numbers. So, 5/1 x 4/4 = 20/4.
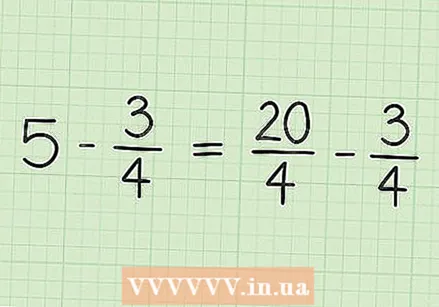3. Rewrite the problem. This can now be noted as: 20/4 - 3/4.
4. Subtract the numerators of the fractions and leave the fractions equal. So, 20 - 3 = 17. So the final numerator becomes 17 and the denominator is 4.
5. The answer to the statement is therefore 17/4. If you want to make a compound fraction of this improper fraction, divide 17 by 4 to get the number 4 with the remainder 1. The answer will look like this: 4 1/4.

Method 6 of 6: Subtracting variables

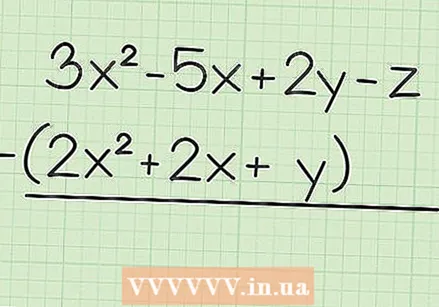1. Write down the statement. Suppose you are working on the following problem: 3x - 5x + 2y - z - (2x + 2x + y). Write the first equation above the second.
2. Subtract all like terms. When working with variables, you can only subtract terms with the same variable and with the same power. This means that you can do 4x -7x, but not 4x -7x. So you can divide this assignment like this:
   • 3x - 2x = x
   • -5x - 2x = -7x
   • 2y - y = y
   • -z - 0 = -z
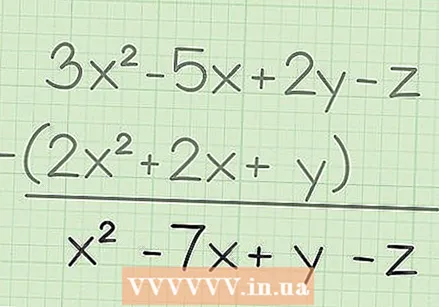3. Give your final answer. Now that you have subtracted all the same terms from each other, you can immediately give your final answer. This is the answer:
   • 3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Tips

• Divide larger numbers into smaller pieces. Take: 63 - 25. Nobody says you should subtract all 25 at once. You can subtract 3 first to get 60; then subtract 20 to get 40 and then the last 2. Result: 38. And now you don't have to borrow.

Warnings

• When you have a mixture of positive and negative numbers, things get a lot trickier. Search for articles that can help you with this.