Content

• To step

Unlike humans, computers do not use the decimal number system. They use a binary or binary number system with two possible digits, 0 and 1. So numbers are written very differently in IEEE 754 (a standard of the IEEE for representing binary numbers with a floating point) than in the traditional decimal system that we to be used to. In this article you will learn how to write a number in either single or double precision according to the IEEE 754. For this method you need to know how to convert numbers to binary form. If you don't know how to do this, you can learn this by studying the article Converting Binary to Decimal.

To step

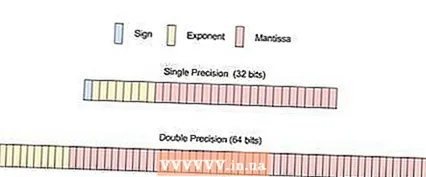1. Choose single or double precision. When writing a number in single or double precision, the steps to a successful conversion will be the same for both. The only change takes place in converting the exponent and the mantissa.
   • First we need to understand what single precision means. In the floating point representation, any number (0 or 1) is considered a "bit". Therefore, a single precision has a total of 32 bits divided into three different subjects. These subjects consist of a sign (1 bit), an exponent (8 bits) and a mantissa or fraction (23 bits).
   • Double precision, on the other hand, has the same setup and the same three parts as single precision - the only difference is that it will be a larger and more accurate number. In this case the sign will have 1 bit, the exponent 11 bits and the mantissa 52 bits.
   • In this example we are going to convert the number 85.125 to single precision according to the IEEE 754.
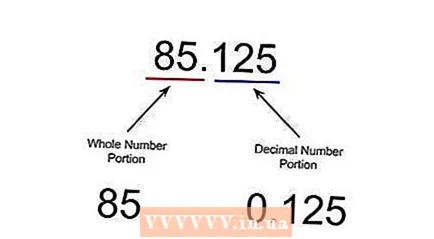2. Separate the number before and after the comma. Take the number you want to convert and separate it so that you are left with a whole number and a decimal number. In this example, we assume the number 85,125. You can separate this into the integer 85 and the decimal 0.125.
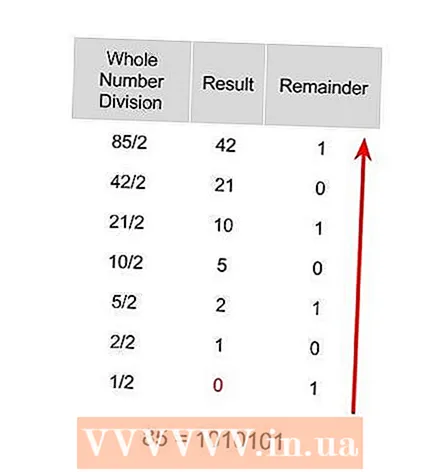3. Convert the whole number to a binary number. This becomes the 85 of 85.125, which will become 1010101 when converted to binary.
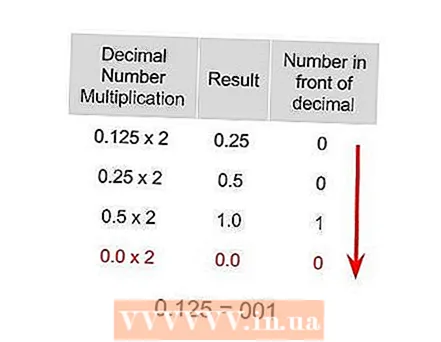4. Convert the decimal part to a binary number. This is 0.125 of 85.125, which becomes 0.001 in binary format.
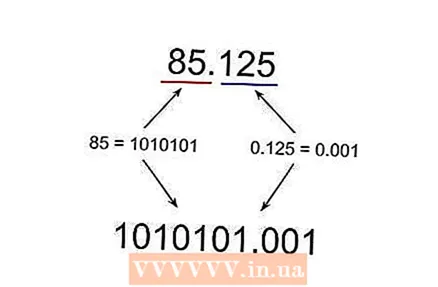5. Combine the two parts of the number that have been converted to binary numbers. The number 85 is binary, for example 1010101 and the decimal part 0.125 is binary 0.001. If you combine them with a decimal point, you get 1010101.001 as the final answer.
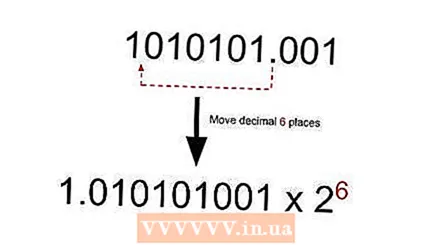6. Convert the binary number to binary scientific notation. You can convert the number to binary scientific notation by moving the decimal point to the left until it is to the right of the first bit. These numbers are normalized, which means that the leading bit will always be 1. As for the exponent, the number of times you move the decimal is the exponent in binary scientific notation.
   • Remember, moving the decimal to the left produces a positive exponent, while moving the decimal to the right produces a negative exponent.
   • In our example, you have to move the decimal six times to get it to the right of the first bit. The resulting format then becomes 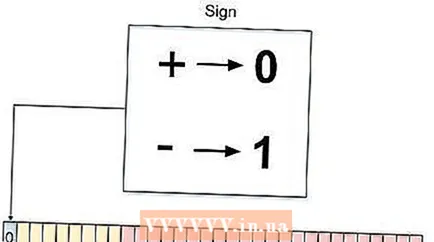${ displaystyle 01.010101001 * 2 ^ {6}}$Determine the sign of the number and display it in binary format. You will now determine whether the original number is positive or negative. If the number is positive, write that bit as 0 and if it is negative, as 1. Since the original number is 85.125 positive, write that bit as 0. This is now the first bit of the total of 32 bits in your single precision rendering according to IEEE 754.
   • Determine the exponent based on the precision. There is fixed bias for both single and double precision. The exponent bias for single precision is 127, which means we have to add the previously found binary exponent. So the exponent you are going to use is 127 + 6 = 133.
     • Double precision, as the name implies, is more accurate and can hold larger numbers. Hence, the bias of the exponent 1023. The same steps used for single precision apply here, so the exponent you can use to determine double precision is 1029.
   • Convert the exponent to binary. After you determine your final exponent, you need to convert it to binary so that it can be used in the IEEE 754 conversion. In the example, you can convert the 133 you found in the last step to 10000101.
   • Determine the mantissa. The mantissa aspect, or the third part of the IEEE 754 conversion, is the remainder of the number after the decimal of scientific binary notation. You just omit the 1 in front and copy the decimal part of the number that is multiplied by two. No binary conversion is required! In the example, the mantissa becomes 010101001 of ${ displaystyle 01.010101001 * 2 ^ {6}}$Finally, combine three parts into one number.
     • Finally, you combine everything we have calculated so far in your conversion. The number will first start with a 0 or 1 that you determined in step 7 based on the sign. In the example you start with a 0.
     • Then you have the exponent that you determined in step 9. In the example, the exponent is 10000101.
     • Then comes the mantissa, the third and last part of the conversion. You deduced this earlier when you took the decimal part of the binary conversion. In the example, the mantissa is 010101001.
     • Finally, you combine all these numbers with each other. The sequence is sign-exponent-mantissa. After connecting these three binary numbers, fill in the rest of the mantissa with zeros.
     • For example, converting 85.125 to the binary IEEE 754 format is the solution 0 10000101 01010100100000000000000.