Content

• To step
• Method 1 of 4: Try to divide
• Method 2 of 4: Using Fermat's little theorem
• Method 3 of 4: Using the Miller-Rabin Test
• Method 4 of 4: Using the Chinese remainder theorem
• Tips
• Necessities

Prime numbers are numbers that are only divisible by themselves and are called 1 - other numbers compound numbers. When it comes to testing whether a number is prime, there are several options. Some of these methods are relatively simple but not at all practical for larger numbers. Other tests that are often used are actually complete algorithms based on one probability who sometimes mistakenly regard a number as prime. Read on to step 1 to learn how to test yourself if you are dealing with a prime number.

To step

Method 1 of 4: Try to divide

Trying to divide is by far the easiest way to test a number. For small numbers it is usually also the fastest way. The test is based on the definition of a prime number: a number is prime if it is only divisible by itself and 1.

1. Suppose n is the number you want to test. Divide the number n by all possible divisible integers. For larger numbers such as n = 101, it is hugely impractical to divide by any possible integer less than n. Fortunately, there are several tricks to reduce the number of factors to be tested.
2. Determine if n even. All even numbers are completely divisible by 2. Therefore, if n is even, you can say that n is a composite number (and therefore not a prime number). To quickly determine whether a number is even, you only have to pay attention to the last digit. If the last digit is a 2, 4, 6, 8 or 0, then the number is even and not prime.
   • The only exception to this rule is the number 2 itself, which, because it is divisible by itself and 1, is also prime. 2 is the only even prime.
3. Part n by any number between 2 and n-1. Because a prime number has no factors other than itself and 1, and because integer factors are less than their product, checking the divisibility of an integer less than n and greater than 2 will determine whether n is prime. We start after 2 because even numbers (multiples of 2) cannot be prime numbers. This is far from an efficient way to test, as you will see below.
   • For example, if we wanted to use this method to test whether 11 is prime or not, we would divide 11 by 3, 4, 5, 6, 7, 8, 9, and 10, looking for a number each time. integer answer without remainder. Since none of these numbers fit completely into 11, we can say that 11 is one is prime.
4. To save time, only test up to sqrt (n), rounded up. Testing a number n by checking all numbers between 2 and n-1 can quickly take a lot of time. For example, if we wanted to check if 103 is prime with this method, we would have to divide by 3, 4, 5, 6, 7 ... etc, all the way to 102! Fortunately, it is not necessary to test like this. In practice, it is only necessary to test for the factors between 2 and the square root of n. If the square root of n is not a number, round it to the nearest integer and test to this number. See below for an explanation:
   • Let's examine the factors of 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2 and 100 × 1. Note that after 10 × 10, the factors are the same if that for 10 × 10, only then flipped. In general, we can ignore the factors of n greater than sqrt (n) as they are simply a continuation of factors less than sqrt (n).
   • Let's try an example. If n = 37, then we don't need to test all numbers from 3 to 36 to determine if n is prime. Instead, we just need to look at the numbers between 2 and sqrt (37) (rounded up).
     • sqrt (37) = 6.08 - we're going to round this up to 7.
     • 37 is not completely divisible by 3, 4, 5, 6, and 7 and so we can confidently state that it is one prime number is.
5. To save even more time, we only use prime factors. It is possible to make the process of testing by dividing even shorter by not including those factors that are not prime numbers. By definition, every composite number can be expressed as the product of two or more prime numbers. So dividing the number n by a composite number is unnecessary - this is equivalent to dividing by prime numbers several times. So, we can further narrow the list of possible factors to only prime numbers less than sqrt (n).
   • This means that all even factors, as well as the factors that are multiples of prime numbers, can be skipped.
   • For example, let's try to determine whether 103 is prime or not. The square root of 103 is 11 (rounded up). The prime numbers between 2 and 11 are 3, 5, 7 and 11. 4, 6, 8 and 10 are even and 9 is a multiple of 3, a prime number, so we can skip it. By doing this we've reduced our list of possible factors to just 4 numbers!
     • 103 is not completely divisible by either 3, 5, 7 or 11, so we now know that 103 is one prime number is.

Method 2 of 4: Using Fermat's little theorem

In 1640, the French mathematician Pierre de Fermat first proposed a theorem (now named after him) that can be very helpful in determining whether or not a number is prime. Technically, Fermat's test is intended to verify that a number is composite, rather than prime. This is because the test can show with "absolute certainty" that a number is composite, but only a "probability" that a number is prime. Fermat's little theorem is useful in situations where trying to divide is impractical and when there is a list of numbers available that are exceptions to the theorem.

1. Suppose n the number is for testing. You use this test to determine whether a given number n is prime. However, as noted above, this theorem may occasionally erroneously characterize some compound as prime. It is important to take this into account and check your answer, which is explained below.
2. Choose an integer a between 2 and n-1 (inclusive). The exact whole number you choose is not important. Since the parameters for a include 2 and n-1, you can also use them.
   • An example: Is 100 a prime number or not. Suppose we take 3 as a test value - this is between 2 and n-1, so that is sufficient.
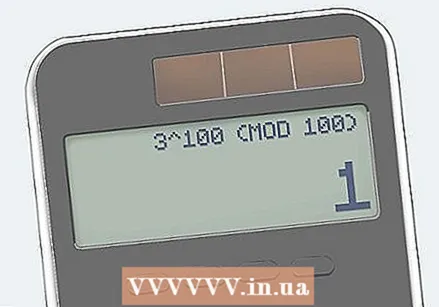3. calculate a (mod n). Working out this expression requires some knowledge of a mathematical system called modular math. In modular math, numbers return to zero upon reaching a certain value, also known as the modulus. You can think of this like a clock: eventually the hand of the clock will return to 1 o'clock after 12 o'clock, not to 13 o'clock. The modulus is noted as (mod n). So in this step you calculate a with a modulus of n.
   • Another method is to calculate a, then divide it by n, then use the remainder as your answer. Specialized calculators with a modulus function can be very useful when dividing large numbers, because they can immediately calculate the remainder of a division.
   • Using such a calculator in our example, we can see that 3/100 has a remainder of 1. So, 3 (mod 100) is 1.
4. If we calculate this by hand, we use the exponent as a short format. If you don't have a calculator with a modulus function, use the notation with an exponent to make the procedure for determining the remainder easier. See below:
   • In our example, we calculate 3 with a modulus of 100. 3 is a very, very large number - 515,377,520,732,011,331,036,461,129,765,621,272,702,107,522,001 - so large that it becomes very difficult to work with. Rather than using the 48-digit answer for 3, we better write it as an exponent, so (((((((3)*3))))*3)). Remember, taking the exponent of an exponent has the effect of multiplying the exponents ((x) = x).
     • Now we can determine the rest. Start by solving ((((((3) * 3)))) * 3)) at the inner set of parentheses and work your way out, dividing each step by 100. Once we've found the rest, we'll use that for the next step instead of the actual answer. See below:
       • ((((((9) * 3)))) * 3)) - 9/100 has no remainder, so we can continue.
       • (((((27)))) * 3)) - 27/100 has no remainder, so we can move on.
       • ((((729))) * 3)) - 729/100 = 7 R 29. Our remainder is 29. We continue with the next step, not 729.
       • ((((29=841)) * 3)) - 841/100 = 8 R 41. We use our remainder 41 again in the next step.
       • (((41 = 1681) * 3)) - 1681/100 = 16 R 81. We use our remainder 81 in the next step.
       • ((81*3 = 243)) - 243/100 = 2 R 43. We'll use our remainder 43 in the next step.
       • (43 = 1849) - 1849/100 = 18 R 49. We'll use our remainder 49 in the next step.
       • 49 = 2401 - 2401/100 = 24 R 1. our final remainder is 1. In other words, 3 (mod 100) = 1. Note that this is the same answer as we calculated in the previous step!
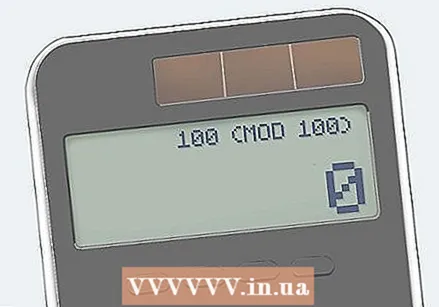5. Find out if a (mod n) = a (mod n). If not, n is compound. If true then n probably, (but not sure) a prime number. Repeating the test with different values ​​for a can make the outcome more certain, but there are rare composite numbers that satisfy Fermat's theorem for all values ​​of a. These are called the Carmichael numbers - the smallest of these numbers is 561.
   • In our example, 3 (mod 100) = 1 and 3 (mod 100) = 3.1 ≠ 3, so we can say that 100 is a composite number.
6. Use the Carmichael numbers to be sure of your outcome. Knowing which numbers meet the Carmichael series before proceeding can save you a lot of worry about whether or not a number is prime. In general, Carmichael numbers are the product of individual prime numbers, where for all prime numbers it holds that if p is a divisor of n, then also p-1 is a divisor of n-1. The online list of Carmichael numbers can be very useful for determining whether a number is prime, using Fermat's Small Theorem.
   
   

Method 3 of 4: Using the Miller-Rabin Test

The Miller-Rabin test works in the same way as Fermat's small theorem, but deals better with non-standard numbers such as Carmichael numbers.

1. Suppose n is an odd number which we want to test for primality. As in the methods indicated above, n is the variable of which we want to determine the primality.
2. Pressure n-1 in the form 2 × d at which d is odd. The number n is prime if it is odd. So n - 1 must be even. Since n - 1 is even, it can be written as a power of 2 times an odd number. So, 4 = 2 × 1; 80 = 2 × 5; and so on.
   • Suppose we want to determine whether n = 321 is prime. 321 - 1 = 320, which we can express as 2 × 5.
     • In this case n = 321 is a suitable number. Determining n - 1 for n = 371 may require a large value for d, making the whole process more difficult at a later stage. 371 - 1 = 370 = 2 × 185
3. Pick any number a between 2 and n-1. The exact number you choose doesn't matter - just that it must be less than n and greater than 1.
   • In our example with n = 321, we choose a = 100.
4. calculate a (mod n). If a = 1 or -1 (mod n), then passes n the Miller-Rabin test and is probably a prime number. As with Fermat's Small Theorem, this test cannot determine with absolute certainty the primality of a number, but requires additional tests.
   • In our example with n = 321, a (mod n) = 100 (mod 321). 100 = 10,000,000,000 (mod 321) = 313. We use a special calculator, or the shorthand method with an exponent as described earlier, to find the remainder of 100/321.
     • Since we have not obtained 1 or -1, we cannot say with certainty that n is prime. But there is still more we need to do - read on.
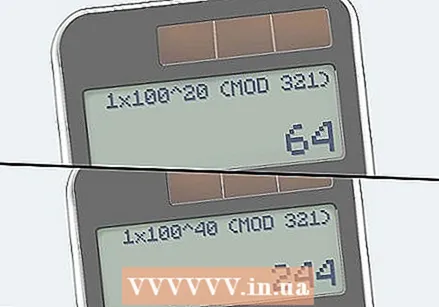5. Since the result is not equal to 1 or -1, calculate a, a, ... and so on, up to ad. Calculate a raised to the power of d times, up to 2. If either of these equals 1 or -1 (mod n), then passes n the Miller-Rabin tests and is probably prime. If you have determined that n passes the test, then check your answer (see the step below). If n fails any of these tests, it is one composed number.
   • As a reminder, in our example, the value of a is 100, the value of s is 6, and d is 5. We continue testing as shown below:
     • 100 = 1 × 10.
       • 1 × 10 (mod 321) = 64.64 ≠’ 1 or -1. Keep going calmly.
     • 100 = 1 × 10.
       • 1 × 10 (mod 321) = 244.244 ≠ 1 or -1.
     • At this point we can stop. s - 1 = 6 - 1 = 5. We have now reached 4d = 2, and there are no powers of 2 times d below 5d. Since none of our calculations answered a 1 or -1, we can say that n = 321 one composed number is.
6. If n passes the Miller-Rabin test, repeat for the other values ​​of a. If you have found that the value of n could be prime, try again with a different, random value for a to confirm the result of the test. If n is actually prime, it will be true for any value of a. If n is a composite number, it will fail for three-quarters of the values ​​of a. This gives you more certainty than Fermat's Small Theorem, where certain composite numbers (the Carmichael numbers) pass the test for any value of a.

Method 4 of 4: Using the Chinese remainder theorem

1. Pick two numbers. One of the numbers is not prime and the second is the number being tested for primality.
   • "Test Number1" = 35
   • Test number2 = 97
2. Choose two data points greater than zero and less than TestNumber1 and TestNumber2, respectively. They cannot be equal to each other.
   • Data1 = 1
   • Data2 = 2
3. Calculate the MMI (Mathematical Multiplicative Inverse) for TestNumber1 and TestNumber2
   • Calculate the MMI
     • MMI1 = Test Number2 ^ -1 Mod Test Number1
     • MMI2 = Test Number1 ^ -1 Mod Test Number2
   • For prime numbers only (there will be an outcome for non-prime numbers, but that's not the MMI):
     • MMI1 = (TestNumber2 ^ (TestNumber1-2))% TestNumber1
     • MMI2 = (TestNumber1 ^ (TestNumber-2))% TestNumber2
   • So:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. Create a binary table for each MMI up to Log2 of the Modulus
   • For the MMI1
     • F (1) = Test Number2% Test Number1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Test Number1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Test Number1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Test Number1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Test Number1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Test Number1 = 1 * 1% 35 = 1
   • Calculate the binary logarithm of TestNumber1 - 2
     • 35 -2 = 33 (10001) base 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 Mod 35
     • MMI1 = 27
   • For MMI2
     • F (1) = Test Number1% Test Number2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Test Number2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Test Number2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Test Number2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Test Number2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Test Number2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Test Number2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Test Number2 = 35 * 35 mod 97 = 61
   • Calculate the binary logarithm of TestNumber2 - 2
     • 97 - 2 = 95 = (1011111) base 2
     • MMI2 = ((((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. Calculate (Data1 * TestNumber2 * MMI1 + Data2 * TestNumber1 * MMI2)% (TestNumber1 * TestNumber)
   • Answer = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Answer = (2619 + 4270)% 3395
   • Answer = 99
6. Check that "TestNumber1" is not prime1
   • Calculate (Answer - Data1)% Test Number1
   • 99 -1 % 35 = 28
   • Since 28 is greater than 0, 35 is not prime
7. Check if TestNumber2 is prime
   • Calculate (Answer - Data2)% Test Number2
   • 99 - 2 % 97 = 0
   • Since 0 equals 0, 97 is a potential prime number
8. Repeat steps 1 to 7 at least two more times.
   • If step 7 equals 0:
     • Use a different "TestNumber1" if TestNumber1 is not prime.
     • Use another TestNumber1 where a TestNumber1 is actually prime. In this case, steps 6 and 7 are equal to 0.
     • Use different data points for data1 and data2.
   • If step 7 is always equal to 0, then the probability that number 2 is a prime number is very high.
   • Steps 1 through 7 are known to be incorrect in certain cases when the first number is not prime and the second is a prime factor of the non-prime number "Test Number1". It works in all scenarios where both numbers are prime.
   • The reason steps 1 through 7 are repeated is because there are a few scenarios where, even if TestNumber1 is not prime and TestNumber2 is not prime, either number from Step 7 is still zero. These conditions are rare. By changing TestNumber1 to another non-prime number, if TestNumber2 is not prime, TestNumber2 will no longer equal zero, in step 7. Except for the case where "TestNumber1" is a factor of TestNumber2, prime numbers will always be zero. are in step 7.

Tips

• The 168 prime numbers under 1000 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
• When trying to divide is slower than the more sophisticated methods, it is still efficient for smaller numbers. Even when testing larger numbers, it is not uncommon to check the small numbers first before switching to the more advanced methods.

Necessities

• Paper, pen, pencil and / or calculator for working out