Content

• Steps
• Method 1 of 4: Calculating the Correlation Coefficient Manually
• Method 2 of 4: Using Online Calculators to Calculate the Correlation Coefficient
• Method 3 of 4: Using a Graphing Calculator
• Method 4 of 4: Explaining Basic Concepts
• Tips
• Warnings

The correlation coefficient (or linear correlation coefficient) is denoted as "r" (in rare cases as "ρ") and characterizes the linear correlation (that is, the relationship that is given by some value and direction) of two or more variables. The value of the coefficient lies between -1 and +1, that is, the correlation can be both positive and negative. If the correlation coefficient is -1, there is a perfect negative correlation; if the correlation coefficient is +1, there is a perfect positive correlation. Otherwise, there is a positive correlation between the two variables, a negative correlation, or no correlation. The correlation coefficient can be calculated manually using free online calculators or with a good graphing calculator.

Steps

Method 1 of 4: Calculating the Correlation Coefficient Manually

1. 1 Collect data. Before you start calculating the correlation coefficient, study these pairs of numbers. Better to write them down in a table that can be arranged vertically or horizontally. Label each row or column with "x" and "y".
   • For example, given four pairs of values ​​(numbers) of the variables "x" and "y". You can create the following table:
     • x || y
     • 1 || 1
     • 2 || 3
     • 4 || 5
     • 5 || 7
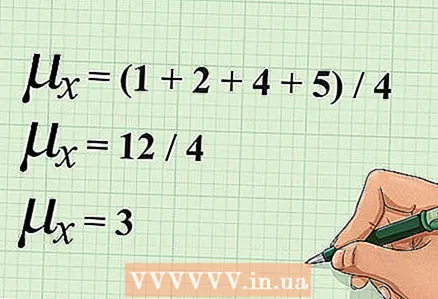2. 2 Calculate the arithmetic mean "x". To do this, add up all the x values, and then divide the result by the number of values.
   • In our example, there are four values ​​for the variable "x". To calculate the arithmetic mean "x", add these values, and then divide the sum by 4. The calculations are written as follows:
   • ${ displaystyle mu _ {x} = (1 + 2 + 4 + 5) / 4}$
   • ${ displaystyle mu _ {x} = 12/4}$
   • ${ displaystyle mu _ {x} = 3}$
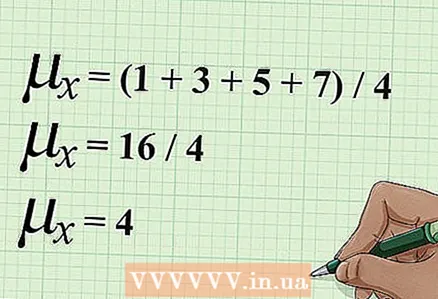3. 3 Find the arithmetic mean "y". To do this, follow the same steps, that is, add up all the y values, and then divide the sum by the number of values.
   • In our example, four values ​​of the variable "y" are given. Add these values, and then divide the sum by 4. The calculations will be written as follows:
   • ${ displaystyle mu _ {y} = (1 + 3 + 5 + 7) / 4}$
   • ${ displaystyle mu _ {y} = 16/4}$
   • ${ displaystyle mu _ {y} = 4}$
4. 4 Calculate the standard deviation "x". After calculating the means of "x" and "y", find the standard deviations of these variables. The standard deviation is calculated using the following formula:
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {n-1}} Sigma (x- mu _ {x}) ^ {2}}}}$
   • In our example, the calculations will be written like this:
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {4-1}} * ((1-3) ^ {2} + (2-3) ^ {2} + ( 4-3) ^ {2} + (5-3) ^ {2})}}}$
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {3}} * (4 + 1 + 1 + 4)}}}$
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {3}} * (10)}}}$
   • ${ displaystyle sigma _ {x} = { sqrt { frac {10} {3}}}}$
   • ${ displaystyle sigma _ {x} = 1.83}$
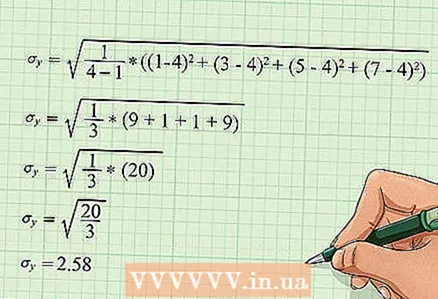5. 5 Calculate the standard deviation "y". Follow the steps outlined in the previous step. Use the same formula, but plug in the y values.
   • In our example, the calculations will be written like this:
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {4-1}} * ((1-4) ^ {2} + (3-4) ^ {2} + ( 5-4) ^ {2} + (7-4) ^ {2})}}}$
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {3}} * (9 + 1 + 1 + 9)}}}$
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {3}} * (20)}}}$
   • ${ displaystyle sigma _ {y} = { sqrt { frac {20} {3}}}}$
   • ${ displaystyle sigma _ {y} = 2.58}$
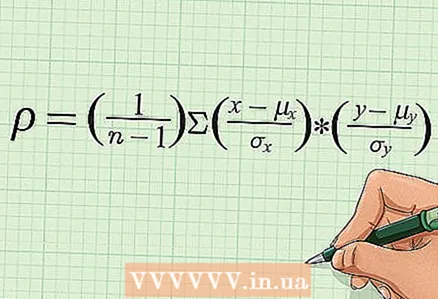6. 6 Write down the basic formula for calculating the correlation coefficient. This formula includes the means, standard deviations, and the number (n) of pairs of numbers of both variables. The correlation coefficient is denoted as "r" (in rare cases as "ρ"). This article uses a formula to calculate the Pearson correlation coefficient.
   • ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } right) * left ({ frac {y- mu _ {y}} { sigma _ {y}}} right)}$
   • Here and in other sources, quantities can be denoted in different ways. For example, some formulas contain “ρ” and “σ”, while others contain “r” and “s”. Some textbooks give different formulas, but they are mathematical counterparts to the above formula.
7. 7 Calculate the correlation coefficient. You have calculated the means and standard deviations of both variables, so you can use the formula to calculate the correlation coefficient. Recall that "n" is the number of pairs of values ​​for both variables. Other values ​​have been calculated earlier.
   • In our example, the calculations will be written like this:
   • ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } right) * left ({ frac {y- mu _ {y}} { sigma _ {y}}} right)}$
   • ${ displaystyle rho = left ({ frac {1} {3}} right) *}$[${ displaystyle left ({ frac {1-3} {1.83}} right) * left ({ frac {1-4} {2.58}} right) + left ({ frac {2-3} {1.83}} right) * left ({ frac {3-4} {2.58}} right)}$
        ${ displaystyle + left ({ frac {4-3} {1.83}} right) * left ({ frac {5-4} {2.58}} right) + left ( { frac {5-3} {1.83}} right) * left ({ frac {7-4} {2.58}} right)}$]
   • ${ displaystyle rho = left ({ frac {1} {3}} right) * left ({ frac {6 + 1 + 1 + 6} {4.721}} right)}$
   • ${ displaystyle rho = left ({ frac {1} {3}} right) * 2.965}$
   • ${ displaystyle rho = left ({ frac {2,965} {3}} right)}$
   • ${ displaystyle rho = 0.988}$
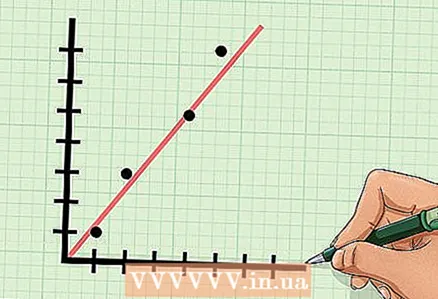8. 8 Analyze the result. In our example, the correlation coefficient is 0.988. This value in some way characterizes a given set of pairs of numbers. Pay attention to the sign and magnitude of the value.
   • Since the value of the correlation coefficient is positive, there is a positive correlation between the variables "x" and "y". That is, as the value of "x" increases, the value of "y" also increases.
   • Since the value of the correlation coefficient is very close to +1, the values ​​of the variables "x" and "y" are highly correlated. If you put points on the coordinate plane, they will be located close to some straight line.

Method 2 of 4: Using Online Calculators to Calculate the Correlation Coefficient

1. 1 Find a calculator on the Internet to calculate the correlation coefficient. This coefficient is often calculated in statistics. If there are many pairs of numbers, it is almost impossible to calculate the correlation coefficient manually. Therefore, there are online calculators to calculate the correlation coefficient. In a search engine, enter "correlation coefficient calculator" (without quotes).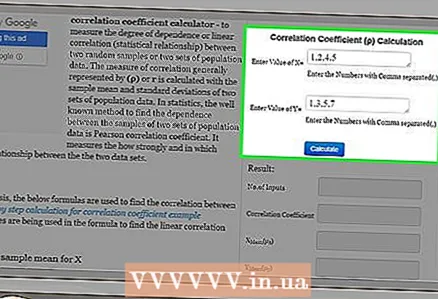
2. 2 Enter data. Check the instructions on the website to enter the correct data (pairs of numbers). It is imperative to enter the appropriate pairs of numbers; otherwise, you will get the wrong result. Remember that different websites have different input formats.
   • For example, at http://ncalculators.com/statistics/correlation-coefficient-calculator.htm, the values ​​of the variables x and y are entered in two horizontal lines. The values ​​are separated by commas. That is, in our example, the values ​​"x" are entered like this: 1,2,4,5, and the values ​​"y" like this: 1,3,5,7.
   • On another site, http://www.alcula.com/calculators/statistics/correlation-coefficient/, data is entered vertically; in this case, do not confuse the corresponding pairs of numbers.
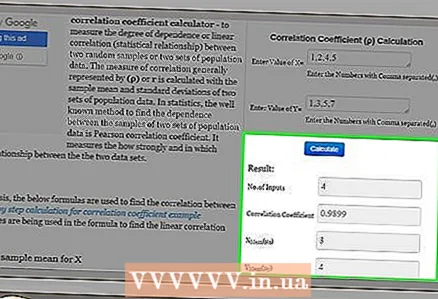3. 3 Calculate the correlation coefficient. After entering the data, simply click on the "Calculate", "Calculate" or similar button to get the result.

Method 3 of 4: Using a Graphing Calculator

1. 1 Enter data. Take a graphing calculator, go into statistical calculation mode and select the "Edit" command.
   • Different calculators require different keys to be pressed. This article discusses the Texas Instruments TI-86 calculator.
   • Press [2nd] - Stat (above the + key) to enter the statistical calculation mode. Then press F2 - Edit.
2. 2 Delete the previously saved data. Most calculators keep the statistics you enter until you erase them. To avoid confusing old data with new ones, first delete any stored information.
   • Use the arrow keys to move the cursor and highlight the 'xStat' heading. Then press Clear and Enter to clear all values ​​entered in the xStat column.
   • Use the arrow keys to highlight the 'yStat' heading. Then press Clear and Enter to clear all values ​​entered in the yStat column.
3. 3 Enter the initial data. Use the arrow keys to move the cursor to the first cell under the heading "xStat". Enter the first value and press Enter. At the bottom of the screen, “xStat (1) = __” is displayed, with the entered value replacing a space. After you press Enter, the entered value will appear in the table, and the cursor will move to the next line; this will display "xStat (2) = __" at the bottom of the screen.
   • Enter all the values ​​for the variable "x".
   • After entering all the values ​​for x, use the arrow keys to navigate to the yStat column and enter the values ​​for y.
   • After entering all pairs of numbers, press Exit to clear the screen and exit the aggregation mode.
4. 4 Calculate the correlation coefficient. It characterizes how close the data is to a certain straight line. The graphing calculator can quickly determine the suitable straight line and calculate the correlation coefficient.
   • Click Stat - Calc. On the TI-86, press [2nd] - [Stat] - [F1].
   • Select the Linear Regression function. On the TI-86, press [F3] which is labeled "LinR". The screen will display the line "LinR _" with a blinking cursor.
   • Now enter the names of two variables: xStat and yStat.
     • On TI-86, open the list of names; to do this, press [2nd] - [List] - [F3].
     • The available variables are displayed on the bottom line of the screen. Select [xStat] (you probably need to press F1 or F2 to do this), enter a comma, and then select [yStat].
     • Press Enter to process the entered data.
5. 5 Analyze your results. By pressing Enter, the screen will display the following information:
   • ${ displaystyle y = a + bx}$: this is the function that describes the line. Please note that the function is not written in standard form (y = kx + b).
   • ${ displaystyle a =}$... This is the y-coordinate of the intersection of the straight line with the y-axis.
   • ${ displaystyle b =}$... This is the slope of the line.
   • ${ displaystyle { text {corr}} =}$... This is the correlation coefficient.
   • ${ displaystyle n =}$... This is the number of pairs of numbers that were used in the calculations.

Method 4 of 4: Explaining Basic Concepts

1. 1 Understand the concept of correlation. Correlation is the statistical relationship between two quantities. The correlation coefficient is a numeric value that can be calculated for any two datasets. The value of the correlation coefficient always lies in the range from -1 to +1 and characterizes the degree of relationship between two variables.
   • For example, given the height and age of children (about 12 years old). Most likely, there will be a strong positive correlation, because children get taller with age.
   • An example of a negative correlation: penalty seconds and time spent in biathlon training, that is, the more an athlete trains, the fewer penalty seconds will be awarded.
   • Finally, there is sometimes very little correlation (positive or negative), such as between shoe size and math scores.
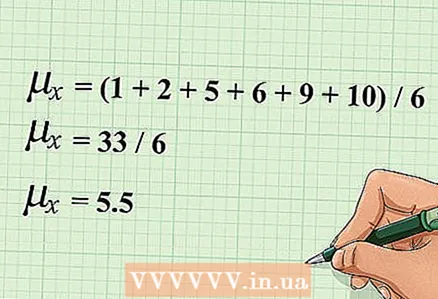2. 2 Remember how to calculate the arithmetic mean. To calculate the arithmetic mean (or mean), you need to find the sum of all these values, and then divide it by the number of values. Remember that the arithmetic mean is needed to calculate the correlation coefficient.
   • The average value of a variable is indicated by a letter with a horizontal bar above it. For example, in the case of variables "x" and "y", their average values ​​are denoted as follows: x̅ and y̅. The mean is sometimes denoted by the Greek letter "μ" (mu). To write the arithmetic mean of the values ​​of the variable "x", use the notation μ_x or μ (x).
   • For example, given the following values ​​for the variable "x": 1,2,5,6,9,10. The arithmetic mean of these values ​​is calculated as follows:
     • ${ displaystyle mu _ {x} = (1 + 2 + 5 + 6 + 9 + 10) / 6}$
     • ${ displaystyle mu _ {x} = 33/6}$
     • ${ displaystyle mu _ {x} = 5.5}$
3. 3 Note the importance of the standard deviation. In statistics, the standard deviation characterizes the degree to which numbers are scattered in relation to their mean. If the standard deviation is small, the numbers are close to the mean; if the standard deviation is large, the numbers are far from the mean.
   • Standard deviation is indicated by the letter "s" or the Greek letter "σ" (sigma). Thus, the standard deviation of the values ​​of the variable "x" is denoted as follows: s_x or σ_x.
4. 4 Remember the symbol for the summation operation. The summation symbol is one of the most common symbols in mathematics and indicates the sum of values. This symbol is the Greek letter "Σ" (uppercase sigma).
   • For example, if given the following values ​​of the variable "x": 1,2,5,6,9,10, then Σx means:
     • 1 + 2 + 5 + 6 + 9 + 10 = 33.

Tips

• The correlation coefficient is sometimes called the "Pearson correlation coefficient" after its developer Carl Pearson.
• In most cases, when the correlation coefficient is greater than 0.8 (positive or negative), there is a strong correlation; if the correlation coefficient is less than 0.5 (positive or negative), a weak correlation is observed.

Warnings

• Correlation characterizes the relationship between the values ​​of two variables. But remember that correlation has nothing to do with causation. For example, if you compare the height and shoe size of people, you are likely to find a strong positive correlation. Generally, the taller the person, the larger the shoe size. But this does not mean that an increase in height leads to an automatic increase in shoe size, or that larger feet will lead to faster growth. These quantities are simply interrelated.