Content

• Steps
• Tips

The rational function has the form y = N (x) / D (x), where N and D are polynomials. To plot such a function accurately, you need a good knowledge of algebra, including differential calculations. Consider the following example: y = (2x - 6x + 5)/(4x + 2).

Steps

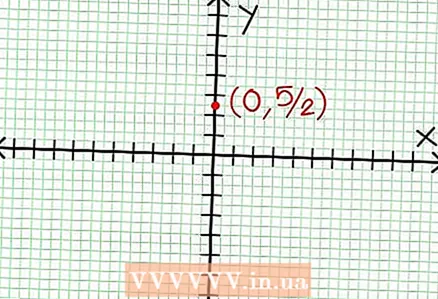1. 1 Find the y-intercept of the graph. To do this, substitute x = 0 into the function and get y = 5/2. Thus, the point of intersection of the graph with the Y axis has coordinates (0, 5/2).Place this point on the coordinate plane.
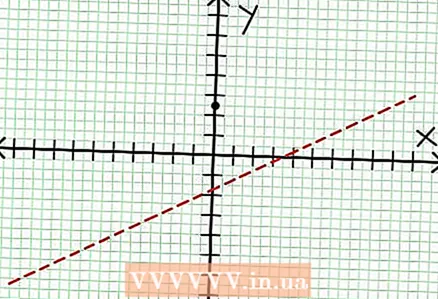2. 2 Find the horizontal asymptotes. Divide the numerator by the denominator (in a column) to determine the behavior of "y" with values ​​of "x" tending to infinity. In our example, the division will be y = (1/2)x - (7/4) + 17/(8x + 4). For large positive or negative values ​​of "x" 17 / (8x + 4) tends to zero, and the graph approaches the straight line given by the function y = (1/2)x - (7/4). Using the dotted line, plot this function.
   • If the degree of the numerator is less than the degree of the denominator, then you cannot divide the numerator by the denominator and the asymptote will be described by the function at = 0.
   • If the degree of the numerator is equal to the degree of the denominator, then the asymptote is a horizontal line equal to the ratio of the coefficients at "x" in the highest degree.
   • If the degree of the numerator is 1 greater than the degree of the denominator, then the asymptote is an inclined straight line, the slope of which is equal to the ratio of the coefficients at "x" to the highest degree.
   • If the degree of the numerator is greater than the degree of the denominator by 2, 3, etc., then for large values ​​|NS| meaning at tend to infinity (positive or negative) in the form of a square, cubic or other degree of a polynomial. In this case, most likely, you do not need to build an exact graph of the function obtained by dividing the numerator by the denominator.
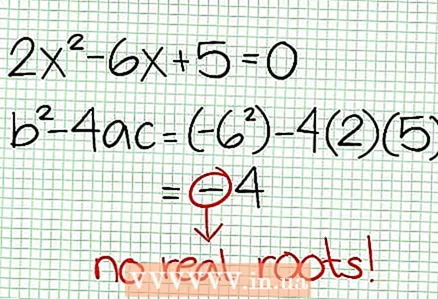3. 3 Find the zeros of the function. A rational function has zeros when its numerator is zero, that is, N (NS) = 0. In our example, 2x - 6x + 5 = 0. The discriminant of this quadratic equation: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Since the discriminant is negative, then N (NS), and hence F (NS) has no real roots. The graph of a rational function does not intersect the X-axis. If the function has zeros (roots), then put them on the coordinate plane.
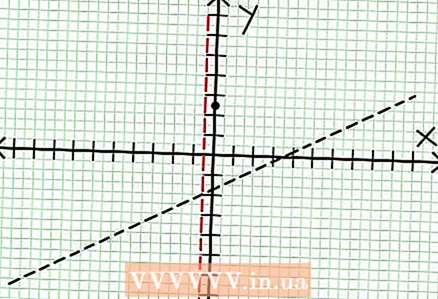4. 4 Find the vertical asymptotes. To do this, set the denominator to zero. In our example, 4x + 2 = 0 and NS = -1/2. Plot the vertical asymptote using the dotted line. If for some value NS N (NS) = 0 and D (NS) = 0, then the vertical asymptote either exists or does not exist (this is a rare case, but it is better to remember it).
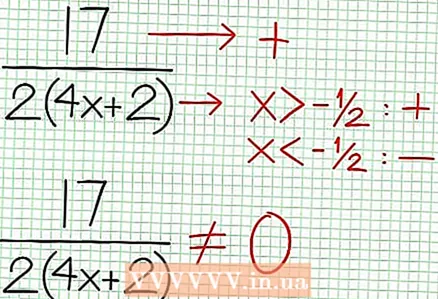5. 5 Look at the remainder of the numerator divided by the denominator. Is it positive, negative, or zero? In our example, the remainder is 17, which is positive. Denominator 4x + 2 positive to the right of the vertical asymptote and negative to the left of it. This means that the graph of the rational function for large positive values NS approaches the asymptote from above, and for large negative values NS - from below. Since 17 / (8x + 4) is never equal to zero, then the graph of this function will never intersect the straight line specified by the function at = (1/2)NS - (7/4).
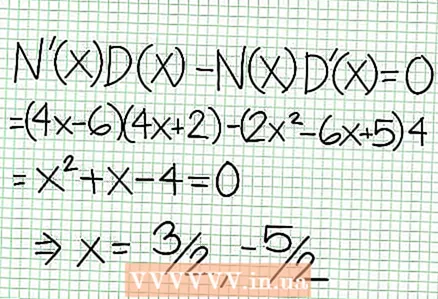6. 6 Find local extrema. A local extremum exists for N '(x) D (x) - N (x) D ’(x) = 0. In our example, N ’(x) = 4x - 6 and D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Solving this equation, you find that x = 3/2 and x = -5/2. (These are not entirely accurate values, but they are suitable for our case, when superprecision is not needed.)
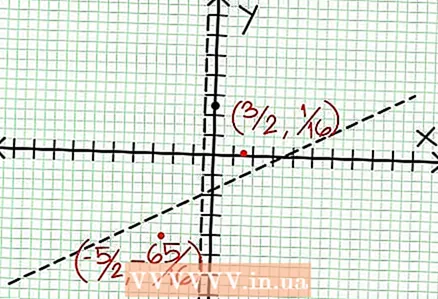7. 7 Find the value at for each local extremum. To do this, substitute the values NS into the original rational function. In our example, f (3/2) = 1/16 and f (-5/2) = -65/16. Set aside points (3/2, 1/16) and (-5/2, -65/16) on the coordinate plane. Since the calculations are based on approximate values ​​(from the previous step), the minimum and maximum found are also not entirely accurate (but probably very close to the exact values). (The point (3/2, 1/16) is very close to the local minimum. Starting from step 3, we know that at always positive for NS> -1/2, and we found a small value (1/16); thus, the error value is extremely small in this case.)
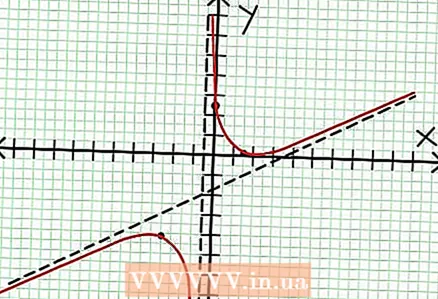8. 8 Connect the pending points and smoothly extend the graph to the asymptotes (do not forget about the correct direction of the graph approaching the asymptotes). Remember that the graph must not cross the X-axis (see step 3). The graph also does not intersect with the horizontal and vertical asymptotes (see step 5). Do not change the direction of the chart except at the extreme points found in the previous step.

Tips

• If you followed the above steps strictly in order, then there is no need to calculate the second derivatives (or similar complex quantities) to test your solution.
• If you do not need to calculate the values ​​of quantities, you can replace finding local extrema by calculating some additional pairs of coordinates (NS, at) between each pair of asymptotes. Moreover, if you do not care how the described method works, then do not be surprised why you cannot find the derivative and solve the equation N '(x) D (x) - N (x) D ’(x) = 0.
• In some cases, you will have to work with higher order polynomials. If you cannot find the exact solution using factorization, formulas, etc., then estimate possible solutions using numerical methods such as Newton's method.
• In rare cases, the numerator and denominator share a common variable factor. According to the steps described, this will lead to zero and a vertical asymptote at the same place. However, this is not possible, and the explanation is one of the following:
  • Zero in N (NS) has a higher multiplicity than zero in D (NS). Graph F (NS) tends to zero at this point, but is not defined there. Indicate this by drawing a circle around the point.
  • Zero in N (NS) and zero in D (NS) have the same multiplicity. The graph approaches some non-zero point at this value NSbut not defined therein. Indicate this by drawing a circle around the point.
  • Zero in N (NS) has a lower multiplicity than zero in D (NS). There is a vertical asymptote here.