Content

• Steps
• Method 1 of 3: Calculating the Slope of the Equation of a Line
• Method 2 of 3: Calculate the Slope Using Two Points
• Method 3 of 3: Using Differential Calculus to Calculate the Slope

The slope characterizes the angle of inclination of the straight line to the abscissa axis (the slope is numerically equal to the tangent of this angle). The slope is present in the equation of a straight line and is used in the mathematical analysis of curves, where it is always equal to the derivative of a function. To make it easier to understand the slope, imagine that it affects the rate of change of the function, that is, the larger the value of the slope, the larger the value of the function (for the same value of the independent variable).

Steps

Method 1 of 3: Calculating the Slope of the Equation of a Line

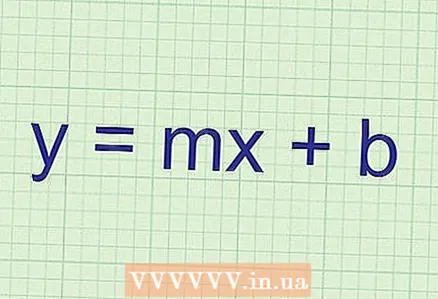1. 1 Use the slope to find the angle of the line to the abscissa and the direction of that line. Calculating the slope is fairly easy if you are given the equation of a straight line. Remember that in any straight line equation:
   • No exponents
   • There are only two variables, none of which is a fraction (for example, such ${ displaystyle { frac {1} {x}}}$)
   • The straight line equation has the form ${ displaystyle y = kx + b}$, where k and b are numerical coefficients (for example, 3, 10, -12, ${ displaystyle { frac {4} {3}}}$).
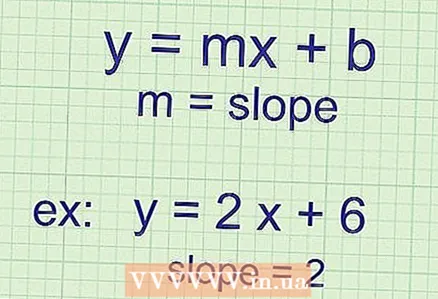2. 2 To find the slope, you need to find the value of k (coefficient at "x"). If the equation given to you has the form ${ displaystyle y = kx + b}$, then to find the slope you just need to look at the number in front of the "x". Note that k (slope) is always at the independent variable (in this case, "x"). If you are confused, check out the following examples:
   • ${ displaystyle y = 2x + 6}$
     • Slope = 2
   • ${ displaystyle y = 2-x}$
     • Slope = -1
   • ${ displaystyle y = { frac {3} {8}} x-10}$
     • Slope = ${ displaystyle { frac {3} {8}}}$
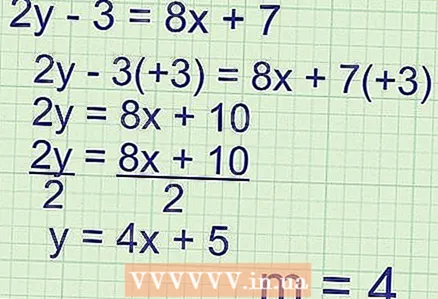3. 3 If the equation given to you has a form other than y=kx+b{ displaystyle y = kx + b}, isolate the dependent variable. In most cases, the dependent variable is denoted as "y", and to isolate it, you can perform operations of addition, subtraction, multiplication, and others. Remember that any mathematical operation must be performed on both sides of the equation (so as not to change its original value). You need to bring any equation given to you to the form ${ displaystyle y = kx + b}$... Let's consider an example:
   • Find the slope of the equation ${ displaystyle 2y-3 = 8x + 7}$
   • It is necessary to bring this equation to the form ${ displaystyle y = kx + b}$:
     • ${ displaystyle 2y-3 (+3) = 8x + 7 (+3)}$
     • ${ displaystyle 2y = 8x + 10}$
     • ${ displaystyle { frac {2y} {2}} = { frac {8x + 10} {2}}}$
     • ${ displaystyle y = 4x + 5}$
   • Finding the slope:
     • Slope = k = 4

Method 2 of 3: Calculate the Slope Using Two Points

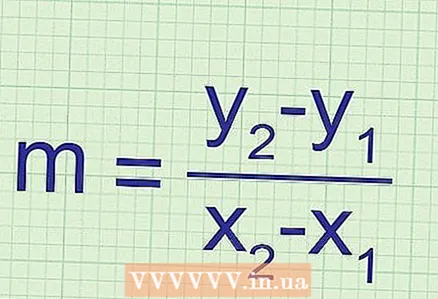1. 1 Use the graph and two dots to calculate the slope. If you are just given a graph of a function (no equation), you can still find the slope. To do this, you need the coordinates of any two points on this graph; coordinates are substituted into the formula: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... To avoid mistakes when calculating the slope, remember the following:
   • If the graph is increasing, then the slope is positive.
   • If the graph is decreasing, then the slope is negative.
   • The higher the slope value, the steeper the graph (and vice versa).
   • The slope of a straight line parallel to the abscissa axis is 0.
   • The slope of a straight line parallel to the ordinate does not exist (it is infinite).
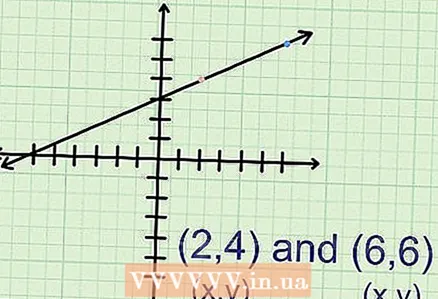2. 2 Find the coordinates of two points. On the graph, mark any two points and find their coordinates (x, y). For example, points A (2.4) and B (6.6) are on the graph.
   • In a pair of coordinates, the first number corresponds to "x" and the second to "y".
   • Each value "x" corresponds to a certain value "y".
3. 3 Equate x₁, y₁, x₂, y₂ to the corresponding values. In our example with points A (2,4) and B (6,6):
   • x₁: 2
   • y₁: 4
   • x₂: 6
   • y₂: 6
4. 4 Plug the found values ​​into the slope formula. To find the slope, the coordinates of two points are used and the following formula is used: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Plug in the coordinates of two points.
   • Two points: A (2.4) and B (6.6).
   • Substitute the coordinates of the points into the formula:
     • ${ displaystyle { frac {6-4} {6-2}}}$
   • Simplify for a definitive answer:
     • ${ displaystyle { frac {2} {4}} = { frac {1} {2}}}$ = Slope
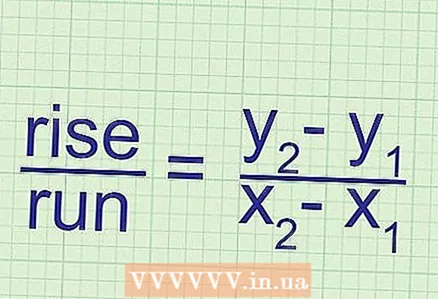5. 5 Explanation of the essence of the formula. The slope is equal to the ratio of the change in the "y" coordinate (two points) to the change in the "x" coordinate (two points). Coordinate change is the difference between the values ​​of the corresponding coordinate of the first and second points.
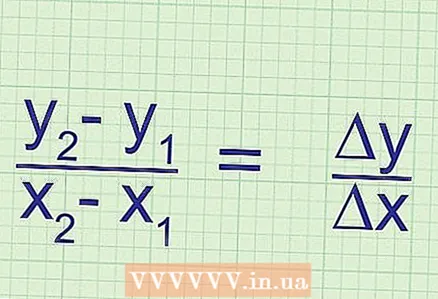6. 6 Another kind of formula for calculating the slope. The standard formula for calculating the slope is: k = ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... But it can be of the following form: k = Δy / Δx, where Δ is the Greek letter "delta", which means difference in mathematics. That is, Δx = x_2 - x_1, and Δy = y_2 - y_1.

Method 3 of 3: Using Differential Calculus to Calculate the Slope

1. 1 Learn to take derivatives from functions. The derivative characterizes the rate of change of a function at a certain point lying on the graph of this function. In this case, the graph can be either a straight or a curved line. That is, the derivative characterizes the rate of change of the function at a particular moment in time. Remember the general rules by which derivatives are taken, and only then proceed to the next step.
   • Read the article How to take a derivative.
   • How to take the simplest derivatives, for example, the derivative of the exponential equation, is described in this article. The calculations presented in the following steps will be based on the methods described in it.
2. 2 Learn to distinguish between problems in which the slope needs to be calculated in terms of the derivative of a function. In problems it is not always proposed to find the slope or the derivative of a function. For example, you may be asked to find the rate of change of a function at point A (x, y). You may also be asked to find the slope of the tangent at point A (x, y). In both cases, it is necessary to take the derivative of the function.
   • For example, find the slope of a function ${ displaystyle f (x) = 2x ^ {2} + 6x}$ at point A (4.2).
   • The derivative is often denoted as ${ displaystyle f ’(x), y’,}$ or ${ displaystyle { frac {dy} {dx}}}$
3. 3 Take the derivative of the function you are given. You don't need to plot a graph here - you only need the equation of the function. In our example, take the derivative of the function ${ displaystyle f (x) = 2x ^ {2} + 6x}$... Take the derivative according to the methods outlined in the article mentioned above:
   • Derivative: ${ displaystyle f ’(x) = 4x + 6}$
4. 4 Substitute the coordinates of the given point into the derived derivative to calculate the slope. The derivative of the function is equal to the slope at a certain point. In other words, f '(x) is the slope of the function at any point (x, f (x)). In our example:
   • Find the slope of the function ${ displaystyle f (x) = 2x ^ {2} + 6x}$ at point A (4.2).
   • Derivative of the function:
     • ${ displaystyle f ’(x) = 4x + 6}$
   • Substitute the value for the x-coordinate of this point:
     • ${ displaystyle f ’(x) = 4 (4) +6}$
   • Find the slope:
   • Slope of function ${ displaystyle f (x) = 2x ^ {2} + 6x}$ at point A (4.2) is 22.
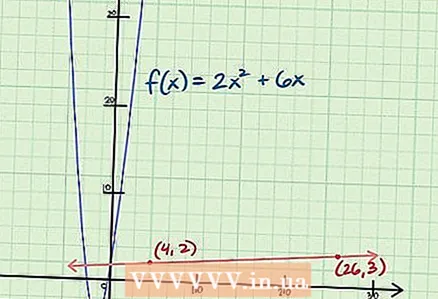5. 5 If possible, check your answer on the graph. Remember that the slope may not be calculated at every point. Differential calculus considers complex functions and complex graphs, where the slope cannot be calculated at every point, and in some cases the points do not lie on the graphs at all. If possible, use a graphing calculator to check that the slope is being calculated correctly for the function given to you.Otherwise, draw a tangent to the graph at the point given to you and consider whether the value of the slope you found matches what you see on the graph.
   • The tangent will have the same slope as the function graph at a particular point. In order to draw a tangent at a given point, move to the right / left along the X-axis (in our example, 22 values ​​to the right), and then up one unit along the Y-axis. Mark the point, and then connect it to the point given to you. In our example, connect the points at coordinates (4,2) and (26,3).