Author:
John Stephens
Date Of Creation:
24 January 2021
Update Date:
1 July 2024

Content
Distance, usually symbolized as d, is the measured length of the line connecting the two points. Distance refers to the space between two fixed points (for example, the height of a person is the distance from the soles of the feet to the top of the head), or refers to the space between the current position of a moving object. with its starting point. Most distance problems can be solved with equations d = savg × t where d is the distance, savg is the average speed, and t is time, or use the equation d = √ ((x2 - x1) + (y2 - y1)), in which (x1, y1) and (x2, y2) is the x and y coordinates of the two points.
Steps
Method 1 of 2: Find your distance with average speed and time

Find the average speed and time. When you want to find the distance an object has moved, there are two values you need to know speed and time its movement. You can then find the distance with the formula d = savg × t.- To better understand the distance method, consider the following example: suppose we are on the road at 193 km / h and want to know how far in half an hour. Use 193 km / h as the value of average speed and 0.5 hour as the time value, the next step is to solve the distance finding problem.

Multiply average velocity by time. Once you know the average speed and travel time of the object, calculating the distance traveled is very simple by multiplying the two values.- Note that if the measurement of time in speed is different from the unit of motion time, you must convert one of the two values to the same unit of time in terms of time. For example, if we have average velocity in km / h and movement time in minutes, then you would have to divide the time by 60 to convert it to hours.
- We all solve the problem as follows. 193 km / hour × 0.5 hours = 96.5 km. Note that the unit in the value of time (hours) is eliminated with the time unit of the average speed in the denominator (hours), so only the distance unit is km.
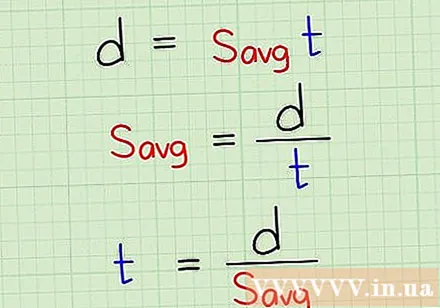
Switch to the equation to find other variables. Because the equation finds the distance (d = savg × t) is so simple that it is easy to switch sides to find variables other than the distance. Keep the desired variable in place and convert the remaining variables to one side of the equation according to the algebraic principle, then insert the values into two known variables to find the third variable. In other words, to find the average speed of an object, we use an equation Savg = d / t and find travel times using the equation t = d / savg.- For example, let's say a car has traveled 60 km in 50 minutes, but we do not know the average speed of the car. So we keep the variable s fixedavg in equation for distance calculation to get equation savg = d / t, then divide 60 km / 50 minutes to find 1.2 km / min.
- Note that the velocity found in the above problem is in uncommon units (km / min). To get the usual speed of km / h, multiply it by 60 minutes / hour and get it 72 km / hour.
The variable "savg"in the distance formula is velocity medium. You should know that the basic distance formula above gives us a simple view of an object's motion. This formula assumes that the object is in motion with constant velocity, that is, it runs at a single speed over the desired distance. For the most common theoretical problems in schools, you can sometimes still simulate the movement of an object using this assumption. However, in practice, such a movement is not accurate because the object will increase and decrease speed, sometimes stop or back.
- For example, in the above problem, we assume that to travel a distance of 60 km in 50 minutes, the car must travel at 72 km / h. This is only true when the vehicle maintains a speed of 72 km / h during the journey. However, if we run 80 km / h on the half trip and 64 km / h on the other half, you will still be going 60 km in 50 minutes, then 72 km / h is not the only result!
- Derivative methods derived from actual computation are a more accurate solution to finding the moving speed of an object in the real world, because in fact velocity is very variable.
Method 2 of 2: Find the distance between two points
Find the spatial coordinates of two points. Instead of finding the distance an object can travel, how would you find the distance between two fixed points? In this case the formula for finding distance based on velocity doesn't help. Fortunately we have a formula for finding the length of a line connecting two points. However, you must know the coordinates of those two points. If you need to find the distance on a single one-way line (as on a coordinate axis), the coordinates of those two points are just x1 and x2. If you need to find distances on a two-dimensional plane, you need the coordinates (x, y) for each point, that is (x1, y1) and (x2, y2). In three dimensions, the coordinate required for each point is (x1, y1, z1) and (x2, y2, z2).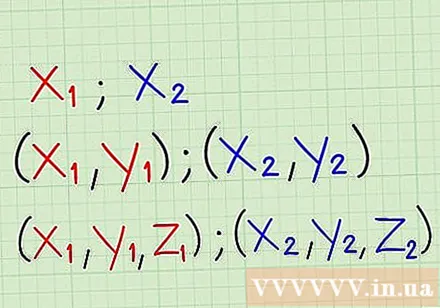
Find the distance on a one-way line by subtracting the coordinates of the two points. Calculate the distance on the line connecting two points knowing their coordinates with the following simple formula d = | x2 - x1|. In this formula, you subtract x1 for x2, then taking the absolute value is the resulting distance between x1 and x2. The calculation of distance on a one-way line usually occurs when two points lie on a number line or a coordinate axis.
- Note that this formula uses the absolute value (the symbol "| |"). Absolute value means that the number in the above symbol will become a positive number if it was previously negative.
- Let's say we stop on a perfectly straight highway. If there is a small town 5 km ahead of us and a town 1 km behind, how far are those two towns? If we set the coordinates for town 1 as x1 = 5 and town 2 is x1 = -1, we have distance d between the two towns as follows:
- d = | x2 - x1|
- =|-1 - 5|
- =|-6| = 6 km.
Find the distance on a two-dimensional plane using the Pythagorean Theorem. Finding the distance between two points in a two-dimensional plane is more complicated than a one-way line, but it's not that difficult. Use the formula d = √ ((x2 - x1) + (y2 - y1)). In this formula, you subtract two x coordinates and square the result, subtract two y coordinates and square the result, then add the two results together and get the square root to get distance between two points. The above formula applies to a two-dimensional plane, for example on an x / y plot.
- The formula for calculating the distance on a 2-dimensional plane uses the Pythagorean theorem, whereby the hypotenuse of a right triangle is equal to the square root of the sum of the squares of the other two sides.
- Suppose we have two points on the x-y plane with coordinates: (3, -10) and (11, 7) correspond to the center of the circle and a point on the circle. To find the straight distance between these two points, we solve the following:
- d = √ ((x2 - x1) + (y2 - y1))
- d = √ ((11 - 3) + (7 - -10))
- d = √ (64 + 289)
- d = √ (353) = 18,79
Find the distance in 3-dimensional space by developing a formula for a 2-dimensional plane. In 3-dimensional space, in addition to the two coordinates x and y, the points also have z coordinates. Use the following formula to find the distance between two points in a space: d = √ ((x2 - x1) + (y2 - y1) + (z2 - z1)). This formula is derived from the formula for the plane by adding the z-coordinate. Subtract two z-coordinates for each other and then square, and continue to do so with the remaining two coordinates, you will surely have a distance between the two points in space.
- Suppose you are an astronaut flying through space, close to two celestial bodies. One celestial body lies 8 km ahead of you, 2 km to the right and 5 km downward, the other 3 km behind you, 3 km to the left and 4 km upwards. Corresponding coordinates of the two celestial bodies are as follows (8,2, -5) and (-3, -3,4), the distance between them will be:
- d = √ ((- 3 - 8) + (-3 - 2) + (4 - -5))
- d = √ ((- 11) + (-5) + (9))
- d = √ (121 + 25 + 81)
- d = √ (227) = 15.07 km