Content

• To step
• Method 1 of 3: A first simple task
• Method 2 of 3: Calculating the expected value for a specific result
• Method 3 of 3: Understand the concept
• Tips
• Necessities

Expectation value is a statistic term, and a concept used to decide how useful or harmful an action will be. In order to calculate the expected value, it is necessary to gain a good understanding of each outcome in a particular situation and the associated probability, or the probability that a particular outcome will occur. The steps below provide some example exercises to help you understand the concept of the expectation value.

To step

Method 1 of 3: A first simple task

1. Read the statement. Before you start thinking about all possible outcomes and probabilities, it is important that you understand the problem. For example a dice game that costs € 10 per game. A hex die is rolled once and your winnings depend on the number you roll. If a 6 is rolled, you win € 30; a 5 earns € 20; any other number does not yield anything.
2. List all possible outcomes. It helps to list all possible outcomes in a given situation. In the example above, there are 6 possible outcomes. These are: (1) roll a 1 and you lose $ 10, (2) roll a 2 and you lose $ 10, (3) roll a 3 and you lose $ 10, (4) roll a 4 and you lose $ 10 , (5) roll a 5 and win $ 10, (6) roll a 6 and win $ 20.
   • Note that each outcome is € 10 less than described above, as you will have to pay € 10 per game first, regardless of the outcome.
3. Determine the probability of each outcome. In this case, the probability of any 6 outcomes is the same. The probability of a random number being rolled is 1 in 6. To make this easier to write down, we will write the fraction (1/6) as a decimal using a calculator: 0.167. Write this probability next to each outcome, especially if you want to solve a problem with different probabilities for each outcome.
   • Your 1/6 calculator might make something like 0.166667. We round this to 0.167 to make it easier to calculate without sacrificing accuracy.
   • If you want a very accurate result, don't make it a decimal, just enter 1/6 into the formula and calculate it on your calculator.
4. Record the value of each outcome. Multiply the $ of a result by the probability that the result will occur to calculate how much money that result will contribute to the expected value. For example, the result of rolling a 1 is - $ 10 and the probability of rolling a 1 is 0.167. The value of throwing a 1 is therefore (-10) * (0.167).
   • There is no need to calculate these results now if you have a calculator that can perform multiple operations at the same time. You will get a more accurate result if you enter the whole equation.
5. Add the value of each outcome to get the expected value of an event. To continue with the above example, the expectation value of the dice game is: (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (10 * 0.167) + (20 * 0.167), or - € 1.67. So you can expect to lose $ 1.67 each time on this game (per game).
6. What are the implications of calculating the expected value. In the example above, we determined that the expected profit (loss) would be - € 1.67 per throw. This is an impossible outcome for 1 game; you can lose € 10, win € 10, or win € 20. But in the long run, the expected value is a useful, average probability. If you keep playing this game, you will lose about $ 1.67 per game, on average. Another way to think about the expected value is by assigning certain costs (or benefits) to the game; you should only play this game if you find it worth it, enjoy it enough to spend $ 1.67 on it every time.
   • The more often a situation is repeated, the more accurately the expected value is a representation of the actual, average outcome. For example, maybe you play the game 5 times in a row and you lose each time, resulting in an average loss of $ 10. However, if you play the game 1000 more times, the average result will come closer and closer to the expected value of - € 1.67 per game. This principle is called "the law of large numbers."

Method 2 of 3: Calculating the expected value for a specific result

1. Use this method to calculate the average number of coins you need to flip before a particular pattern occurs. For example, you can use the method to find out the expected number of coins to flip until you have heads twice in a row. This problem is a bit trickier than a standard problem about expectation values, so read the above part of this article first if you are not familiar with the concept of expectation value.
2. Suppose we are looking for a value x. You are trying to determine how many coins you have to flip on average to get two heads in a row. We now make a comparison to find the answer. We call the answer we are looking for x. We make the necessary comparison step by step. We currently have the following:
   • x = ___
3. Think about what happens if the first flip produces a coin. This will be the case in half of the cases. If this is the case, you have "wasted" a roll over, while the chance to roll a head twice in a row has not changed. As with the coin toss, it is expected that you have to throw an average number of times before you get two heads in a row. In other words, you would expect to roll an x ​​number of times, plus the ones you've already played. In the form of an equation:
   • x = (0.5) (x + 1) + ___
   • We are going to fill in the empty space as we continue to think about other situations.
   • You can use fractions instead of decimals if it is easier or necessary.
4. Think about what happens when you throw your head. There is a 0.5 (or 1/2) chance that you will throw a cup the first time. This seems to get closer to the goal of throwing a head twice in a row, but how much? The easiest way to find out is to think about your options on the second roll:
   • If the second toss is a coin, we're back to the beginning.
   • If the second time is also a cup, then we're done!
5. Learn how to calculate the probability that two events will both occur. We now know that you have a 50% chance that you will throw a cup, but what is the chance that you will throw a cup twice in a row? To calculate this probability, multiply the probability of both. In this case it is 0.5 x 0.5 = 0.25. Of course, this is also the chance that you will roll heads and then tails, because they both have a chance of 0.5 to occur: 0.5 x 0.5 = 0.25.
6. Add the result for "heads, then tails" to the equation. Now that we have calculated the probability that this event will occur, we can move on to expanding the equation. There is a 0.25 (or 1/4) chance that we will waste throwing twice without moving forward. But now we still need an x ​​number of more throws on average to get the result we want to get, plus the 2 we've already thrown. In equation form, this becomes (0.25) (x + 2), which we can now add to the equation:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + ___
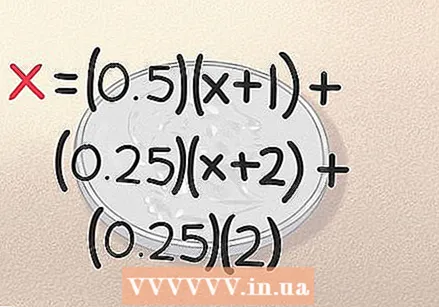7. Add the result for "heading, heading" to the equation. If you roll head, head with the first two toss of the coins, you're done. You got the result in exactly 2 throws. As we noted earlier, there is a 0.25 chance of this happening, so the equation for this is (0.25) (2). Our comparison is now complete:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + (0.25) (2)
   • If you're not sure you've thought through every possible situation, there is an easy way to check that the equation is complete. The first number in each part of the equation represents the probability that an event will occur. This will always add up to 1. Here, 0.5 + 0.25 + 0.25 = 1, so we know we've included every situation.
8. Simplify the equation. Let's make the equation a bit easier by multiplying. Remember, if you see something in parentheses like this: (0.5) (x + 1), then you multiply 0.5 by each term that is in the second set of parentheses. This gives you the following: 0.5x + (0.5) (1), or 0.5x + 0.5. Let's do this for each term in the equation, then combine these terms so that it all looks a bit simpler:
   • x = 0.5x + (0.5) (1) + 0.25x + (0.25) (2) + (0.25) (2)
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0.75x + 1.5
9. Solve for x. As in any equation, you will need to isolate the x on one side of the equation to calculate it. Remember, x means "the average number of coins you need to toss to get heads twice in a row." When we have calculated x, we have also found our answer.
   • x = 0.75x + 1.5
   • x - 0.75x = 0.75x + 1.5 - 0.75x
   • 0.25x = 1.5
   • (0.25x) / (0.25) = (1.5) / (0.25)
   • x = 6
   • On average, you will have to throw a coin 6 times before throwing heads twice.

Method 3 of 3: Understand the concept

1. What is an expected value actually. The expectation value is not necessarily the most obvious or logical result. Sometimes an expectation value can even be an impossible value in a given situation. For example, the expectation value can be + € 5 for a game with a prize of no more than € 10. What the expectation value indicates is how much value a particular event has. If a game has an expected value of + € 5, then you can play it if you feel it is worth the time and money you can get per game. If another game has an expected value of - $ 20, then you only play it if you think each game is worth $ 20.
2. Understand the concept of independent events. In everyday life, many of us think we have a lucky day when some good things happen, and we expect the rest of the day to go that way.In the same way, we can think that we have had enough of an accident and that something fun really needs to be done now. Mathematically, things don't go that way. If you throw a regular coin, there is exactly the same chance that you will throw a head or a coin. It doesn't matter how many times you have already thrown; the next time you throw it still works the same way. The coin toss is "independent" of the other tosses, it is not affected by it.
   • The belief that you can be lucky or unlucky when throwing coins (or any other game of chance), or The fact that all your bad luck has now ended and luck is on your side is also called gambler cheating (or the gambler's fallacy). This has to do with people's tendency to make risky or stupid decisions when they feel that luck is on their side, or if they feel "lucky streak" or if they feel their "luck is about to turn." "
3. Understand the law of large numbers. You might think that the expectation value is not really useful, because it only rarely tells you what the actual outcome of a situation is. If you have calculated that the expected value of a roulette game is - € 1, and you play the game 3 times, you will usually end up with - € 10, or + € 60, or some other result. The "Law of Big Numbers" helps explain why the expectation value is more useful than you might think: the more you play, the closer to the expectation value the average result will be. When you look at the large numbers of events, there is a good chance that the final result is close to the expected value.

Tips

• For those situations where multiple outcomes are possible, you can create a spreadsheet in the computer to calculate the expected value using the outcomes and their probabilities.
• The € calculations above also work in other currencies.

Necessities

• Pencil
• Paper
• Calculator