Content

• To step
• Method 1 of 3: Determine the area using the sides and the apothem
• Method 2 of 3: Determining the area using the length of a side
• Method 3 of 3: Using a formula
• Tips

A pentagon is a polygon with five straight sides. Almost all of the problems you will encounter in math class will involve regular pentagons, with five equal sides. There are two common ways to calculate the area, depending on how much information you have.

To step

Method 1 of 3: Determine the area using the sides and the apothem

1. Start with the length of the side and apothem. This method works for regular pentagons, with five equal sides. In addition to the length of the side, you need the "apothem" of the pentagon. The apothem is the line from the center of the pentagon to a side that intersects the side perpendicularly (ie at an angle of 90º).
   • Do not confuse the apothem with the radius of a polygon, because it intersects an angle (vertex) instead of a point in the center of the side. If you only know the length of one side and the radius, move on to the next method.
   • We use a pentagon with side as an example 3 and apothem 2.
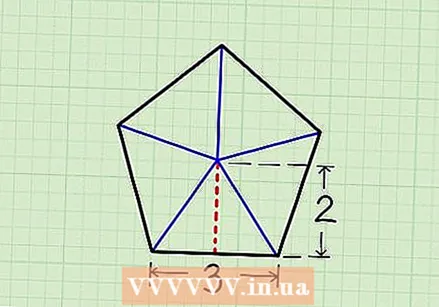2. Divide the pentagon into five triangles. Draw five lines from the center of the pentagon, each leading to a vertex (corner). You now have five triangles.
3. Calculate the area of ​​a triangle. Each triangle has one base equal to the side of the pentagon. It also has one height which is equal to the apothem. (Remember, the height of a triangle is the length of the side that is perpendicular to the base and running to a vertex). To calculate the area of ​​a triangle, use ½ x base x height.
   • In our example, the area of ​​the triangle is = ½ x 3 x 2 =3.
4. Multiply by five for the total area of ​​the pentagon. We have divided the pentagon into five equal triangles. To calculate the total area, multiply the area of ​​a triangle by five.
   • In our example, A (total of the pentagon) = 5 x A (triangle) = 5 x 3 =15.

Method 2 of 3: Determining the area using the length of a side

1. Start with the length of one side. This method only works for regular pentagons, which have five sides of equal length.
   • In this example we will use a pentagon with length 7 for each side.
2. Divide the pentagon into five triangles. Draw a line from the center of the pentagon to a vertex. Repeat this for each vertex. You now have five triangles, each of the same size.
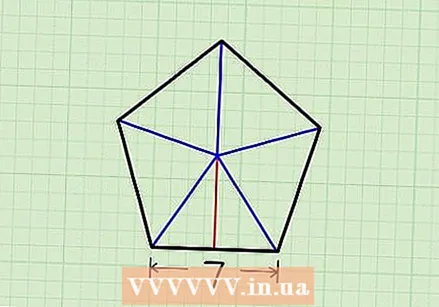3. Divide a triangle in half. Draw a line from the center of the pentagon to the base of a triangle. This line should intersect the base at a right angle (90º), which divides the triangle into two equal, smaller triangles.
4. Label one of the smaller triangles. We can already label a side and an angle of the smaller triangle:
   • The base of the triangle is ½ times the side of the pentagon. In our example, this is ½ x 7 = 3.5 units.
   • The angle in the center of the pentagon is always 36º. (Assuming 360º for a full circle, you can divide this into 10 smaller triangles. 360 ÷ 10 = 36, so the angle of such a triangle is 36º).
5. Calculate the height of the triangle. The height the side of this triangle is perpendicular to the side of the pentagon leading to the center. We use simple trigonometry to determine the length of this side:
   • In a right triangle, the tangent of an angle equal to the length of the opposite side divided by the length of the adjacent side.
   • The side opposite the 36º angle is the base of the triangle (half the side of the pentagon). The adjacent side of the 36º angle is the height of the triangle.
   • tan (36º) = opposite / adjacent
   • In our example, tan (36º) = 3.5 / height
   • height x tan (36º) = 3.5
   • height = 3.5 / tan (36º)
   • height = (approximately) 4,8 .
6. Calculate the area of ​​the triangle. The area of ​​a triangle equals ½ base x its height. (A = ½bh.) Now that you know the height, enter these values ​​to determine the height of your small triangle.
   • In our example, the area of ​​one of the small triangles = ½bh = ½ (3.5) (4.8) = 8.4.
7. Multiply to find the area of ​​the pentagon. One of these smaller triangles covers 1/10 of the area of ​​the pentagon. For the total area, multiply the area of ​​the smaller triangle by 10.
   • In our example, the area of ​​the entire pentagon is = 8.4 x 10 =84.

Method 3 of 3: Using a formula

1. Use the outline and apothem. The apothem is a line from the center of a pentagon that intersects one side at right angles. If the length is given, then you can use this simple formula.
   • Area of ​​a regular pentagon =dad / 2, where p= the circumference and a= the apothem.
   • If you don't know the circumference, calculate it using the length of the side: p = 5s, where s is the length of the side.
2. Use the length of the side. If you only know the length of the sides, use the following formula:
   • Area of ​​a regular pentagon = (5s ) / (4tan (36º)), where s= length of one side.
   • tan (36º) = √ (5-2√5). If your calculator doesn't have a tan function, use the formula for the area: Area = (5s) / (4√(5-2√5)).
3. Choose a formula that uses only the radius. You can even find the area if you only know the radius. Use the following formula:
   • The area of ​​a regular pentagon = (5/2)rsin (72º), where r the radius is.

Tips

• Irregular pentagons or pentagons with unequal sides are more difficult to study. The best approach is usually to divide the pentagon into triangles and add the areas of all triangles. You may also need to draw a larger shape around the pentagon, calculate its area, and then subtract the area of ​​the extra space.
• If possible, use both a geometric method and a formula and compare the results to check your answer. The answers may be slightly different if you fill in the formula completely at once (because the steps in which you complete it are missing), but they should be very close to each other.
• The examples given here use rounded values ​​to make their math easier. If you have a true polygon with the given side lengths, you will get slightly different results for the other lengths and the area.
• The formulas are derived from geometric methods, similar to those described here. Try to figure out how to deduce them yourself. The radius formula is more difficult to derive than the others (hint: you need the double-angle identity).