Content

• Steps
• Method 1 of 4: Calculating the Height of a Rectangular Prism from a Known Volume
• Method 2 of 4: Calculate the Height of a Triangular Prism from a Known Volume
• Method 3 of 4: Calculate the Height of a Rectangular Prism from a Known Surface Area
• Method 4 of 4: Calculate the Height of a Triangular Prism from a Known Surface Area
• Warnings
• What do you need

A prism is a three-dimensional figure with two equal parallel bases. The shape at the base defines the type of prism, for example, rectangular or triangular prism. Since a prism is a volumetric figure, it is often necessary to calculate the volume (the space bounded by the side faces and bases) of the prism. But sometimes in tasks it is required to find the height of the prism.It is not that difficult if the necessary information is given: the volume or surface area and the perimeter of the base. The formulas in this article apply to prisms with bases of any shape if you know how to calculate the area of ​​the base.

Steps

Method 1 of 4: Calculating the Height of a Rectangular Prism from a Known Volume

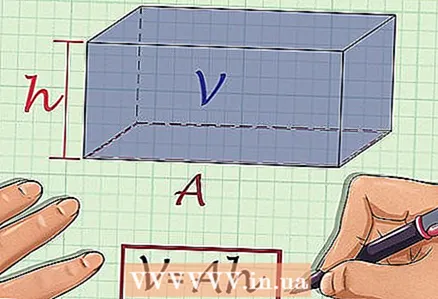1. 1 Write down the formula for calculating the volume of the prism. The volume of any prism can be calculated by the formula ${ displaystyle V = Sh}$, where ${ displaystyle V}$ - the volume of the prism, ${ displaystyle S}$ - base area, ${ displaystyle h}$ Is the height of the prism.
   • The base of the prism is one of the equal faces. Since the opposite faces are equal in a rectangular prism, any face can be considered as the base, but do not confuse the face taken as the base during calculations.
2. 2 Plug in the volume into the formula. If no volume is given, this method cannot be used.
   • Example: the volume of a prism is 64 cubic meters (m); the formula will be written like this:
     ${ displaystyle 64 = Sh}$
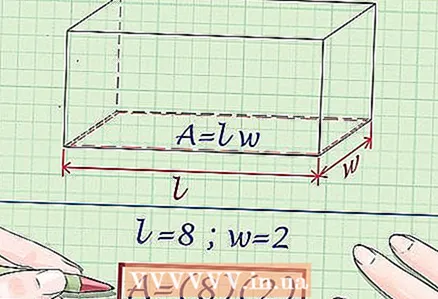3. 3 Calculate the area of ​​the base. To do this, you need to know the length and width of the base (or one of the sides, if the base is a square). To calculate the area of ​​a rectangle, use the formula ${ displaystyle S = lw}$.
   • Example: at the base of the prism there is a rectangle whose sides are equal to 8 m and 2 m.Calculate the area of ​​the rectangle:
     ${ displaystyle S = (8) (2)}$
     ${ displaystyle S = 16}$ m
4. 4 Plug the base area into the prism volume formula. Substitute the area value instead of ${ displaystyle S}$.
   • Example: the base area is 16 m, so the formula will be written like this:
     ${ displaystyle 64 = 16h}$
5. 5 Find h{ displaystyle h}. This will calculate the height of the prism.
   • Example: in the equation ${ displaystyle 64 = 16h}$ divide both sides by 16 to find ${ displaystyle h}$.Thus:
     ${ displaystyle { frac {64} {16}} = { frac {16h} {16}}}$
     ${ displaystyle 4 = h}$
     That is, the height of the prism is 4 m.

Method 2 of 4: Calculate the Height of a Triangular Prism from a Known Volume

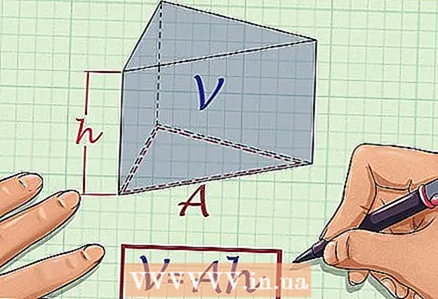1. 1 Write down the formula for calculating the volume of the prism. The volume of any prism can be calculated by the formula ${ displaystyle V = Sh}$, where ${ displaystyle V}$ - the volume of the prism, ${ displaystyle S}$ - base area, ${ displaystyle h}$ Is the height of the prism.
   • The base of the prism is one of the equal faces. The bases of the triangular prism are triangles, and the faces are rectangles.
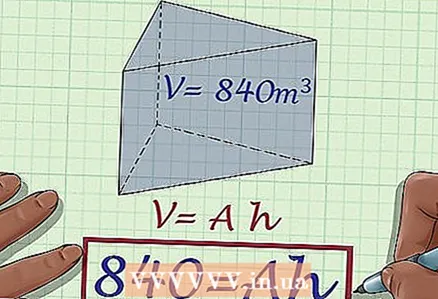2. 2 Plug in the volume into the formula. If no volume is given, this method cannot be used.
   • Example: the volume of a prism is 840 cubic meters (m); the formula will be written like this:
     ${ displaystyle 840 = Sh}$
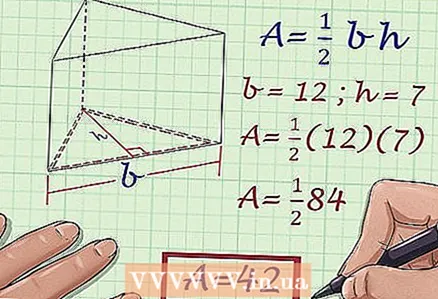3. 3 Calculate the area of ​​the base. To do this, you need to know the height of the triangle and the side to which the height is lowered. To calculate the area of ​​a triangle, use the formula ${ displaystyle S = { frac {1} {2}} (b) (h)}$.
   • Given three sides of a triangle, calculate its area using Heron's formula.
   • Example: the height of a triangle is 7 m, and the side to which the height is lowered is 12 m.Calculate the area of ​​the triangle:
     ${ displaystyle S = { frac {1} {2}} (12) (7)}$
     ${ displaystyle S = { frac {1} {2}} (84)}$
     ${ displaystyle S = 42}$
4. 4 Plug the base area into the prism volume formula. Substitute the area value instead of ${ displaystyle S}$.
   • Example: the base area is 42 m, so the formula will be written like this:
     ${ displaystyle 840 = 42h}$
5. 5 Find h{ displaystyle h}. This will calculate the height of the prism.
   • Example: in the equation ${ displaystyle 840 = 42h}$ divide both sides by 42 to find ${ displaystyle h}$.Thus:
     ${ displaystyle { frac {840} {42}} = { frac {42h} {42}}}$
     ${ displaystyle 20 = h}$
     
   • The height of the prism is 20 m.

Method 3 of 4: Calculate the Height of a Rectangular Prism from a Known Surface Area

1. 1 Write down a formula for calculating the surface area of ​​a prism. The surface area of ​​any prism can be calculated by the formula ${ displaystyle SA = 2S + Ph}$, where ${ displaystyle SA}$ - surface area, ${ displaystyle S}$ - base area, ${ displaystyle P}$ - base perimeter, ${ displaystyle h}$ Is the height of the prism.
   • To use this method, you need to know the surface area of ​​the prism and the length and width of the base.
2. 2 Plug the surface area into the formula. If no surface area is given, this method cannot be used.
   • Example: The surface area of ​​a prism is 1460 square centimeters; the formula will be written like this:
     ${ displaystyle 1460 = 2S + Ph}$
3. 3 Calculate the area of ​​the base. To do this, you need to know the length and width of the base (or one of the sides, if the base is a square). To calculate the area of ​​a rectangle, use the formula ${ displaystyle S = lw}$.
   • Example: at the base of the prism there is a rectangle, the sides of which are 8 cm and 2 cm. Calculate the area of ​​the rectangle:
     ${ displaystyle S = (8) (2)}$
     ${ displaystyle S = 16}$
4. 4 Plug the base area into the formula to calculate the surface area of ​​the prism. Substitute the area value instead of ${ displaystyle S}$.
   • Example: the base area is 16, so the formula will be written like this:
     ${ displaystyle 1460 = 2 (16) + Ph}$
     ${ displaystyle 1460 = 32 + Ph}$
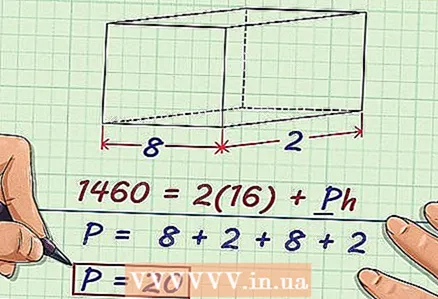5. 5 Find the perimeter of the base. Add the values ​​of all (four) sides to find the perimeter of the rectangle; to find the perimeter of a square, multiply the value of one side by 4.
   • Remember that the opposite sides of the rectangle are equal.
   • Example: The perimeter of a rectangle with sides equal to 8 cm and 2 cm is calculated as follows:
     ${ displaystyle P = 8 + 2 + 8 + 2}$
     ${ displaystyle P = 20}$
6. 6 Plug the base perimeter into the prism surface area formula. Substitute the perimeter value for ${ displaystyle P}$.
   • Example: If the perimeter of the base is 20, the formula will be written like this:
     ${ displaystyle 1460 = 32 + 20h}$
7. 7 Find h{ displaystyle h}. This will calculate the height of the prism.
   • Example: in the equation ${ displaystyle 1460 = 32 + 20h}$ subtract 32 from both sides, and then divide both sides by 20. Thus:
     ${ displaystyle 1460 = 32 + 20h}$
     ${ displaystyle 1428 = 20h}$
     ${ displaystyle { frac {1428} {20}} = { frac {20h} {20}}}$
     ${ displaystyle 71,4 = h}$
   • The height of the prism is 71.4 cm.

Method 4 of 4: Calculate the Height of a Triangular Prism from a Known Surface Area

1. 1 Write down a formula for calculating the surface area of ​​a prism. The surface area of ​​any prism can be calculated by the formula ${ displaystyle SA = 2S + Ph}$, where ${ displaystyle SA}$ - surface area, ${ displaystyle S}$ - base area, ${ displaystyle P}$ - base perimeter, ${ displaystyle h}$ Is the height of the prism.
   • To use this method, you need to know the surface area of ​​the prism, the area of ​​the triangle (which lies at the base), and all the sides of that triangle.
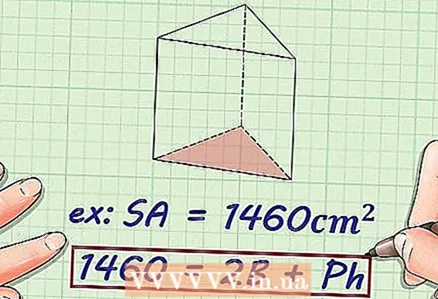2. 2 Plug the surface area into the formula. If no surface area is given, this method cannot be used.
   • Example: The surface area of ​​a prism is 1460 square centimeters; the formula will be written like this:
     ${ displaystyle 1460 = 2S + Ph}$
3. 3 Calculate the area of ​​the base. To do this, you need to know the height of the triangle and the side to which the height is lowered. To calculate the area of ​​a triangle, use the formula ${ displaystyle S = { frac {1} {2}} (b) (h)}$.
   • Given three sides of a triangle, calculate its area using Heron's formula.
   • Example: the height of a triangle is 4 cm, and the side to which the height is lowered is 8 cm. Calculate the area of ​​the triangle:
     ${ displaystyle S = { frac {1} {2}} (8) (4)}$
     ${ displaystyle S = { frac {1} {2}} (32)}$
     ${ displaystyle S = 16}$
4. 4 Plug the base area into the formula to calculate the surface area of ​​the prism. Substitute the area value instead of ${ displaystyle S}$.
   • Example: the base area is 16, so the formula will be written like this:
     ${ displaystyle 1460 = 2 (16) + Ph}$
     ${ displaystyle 1460 = 32 + Ph}$
5. 5 Find the perimeter of the base. Add the values ​​of all (three) sides to find the perimeter of a triangle.
   • Example: The perimeter of a triangle whose sides are 8 cm, 4 cm and 9 cm is calculated as follows:
     ${ displaystyle P = 8 + 4 + 9}$
     ${ displaystyle P = 21}$
6. 6 Plug the base perimeter into the prism surface area formula. Substitute the perimeter value for ${ displaystyle P}$.
   • Example: if the perimeter of the base is 21, the formula will be written like this:
     ${ displaystyle 1460 = 32 + 21h}$
7. 7 Find h{ displaystyle h}. This will calculate the height of the prism.
   • Example: in the equation ${ displaystyle 1460 = 32 + 21h}$ subtract 32 from both sides, and then divide both sides by 21. Thus:
     ${ displaystyle 1460 = 32 + 21h}$
     ${ displaystyle 1428 = 21h}$
     ${ displaystyle { frac {1428} {21}} = { frac {21h} {21}}}$
     ${ displaystyle 68 = h}$
   • The height of the prism is 68 cm.

Warnings

• Do not confuse the height of the triangular prism with the height of the triangle that lies at the base of the prism. The height of a triangle is the perpendicular dropped from any vertex of the triangle to the opposite side, which is called the base of the triangle. The height of an isosceles triangle can be found if the base and side are given. Divide the base by 2 and then use the Pythagorean theorem (${ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$), where but (or b) Is the height of the triangle. Remember: there is no apothem in the prism!

What do you need

• Pen / pencil and paper or calculator (optional)