Content

• Steps
• Part 1 of 3: Tests of Simplicity
• Part 2 of 3: How Simplicity Tests Work
• Part 3 of 3: Using the Chinese Remainder Theorem
• Tips
• What do you need

Prime numbers are numbers that are divisible only by themselves and by 1. All other numbers are called composite numbers. There are many ways to determine if a number is prime, and they all have their own advantages and disadvantages. On the one hand, some of the methods are very accurate, but they are quite complex if you are dealing with large numbers. On the other hand, there are much faster ways, but they can lead to incorrect results. The choice of the appropriate method depends on how large the numbers you are working with.

Steps

Part 1 of 3: Tests of Simplicity

Note: in all formulas n denotes the number to be checked.

1. 1 Enumeration of divisors. It is enough to divide n to all prime numbers from 2 to the rounded value (${ displaystyle { sqrt {n}}}$).
2. 2 Fermat's little theorem. Warning: sometimes the test will falsely identify composite numbers as prime, even for all values ​​of a.
   • Let's choose an integer asuch that 2 ≤ a ≤ n - 1.
   • If a (mod n) = a (mod n), then the number is probably prime. If the equality is not satisfied, the number n is composite.
   • Check given equality for multiple values ato increase the likelihood that the number being tested is indeed prime.
3. 3 Miller-Rabin test. Warning: sometimes, although rarely, for multiple values ​​of a, the test will falsely identify composite numbers as prime.
   • Find the quantities s and d such that ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Select an integer a in the range 2 ≤ a ≤ n - 1.
   • If a = +1 (mod n) or -1 (mod n), then n is probably prime. In this case, go to the test result. If the equality does not hold, go to the next step.
   • Square your answer (${ displaystyle a ^ {2d}}$). If you get -1 (mod n), then n is probably a prime number. In this case, go to the test result. If the equality fails, repeat (${ displaystyle a ^ {4d}}$ and so on) until ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • If at some step after squaring a number other than ${ displaystyle pm 1}$ (mod n), you got +1 (mod n), so n is a composite number. If ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), then n is not prime.
   • Test result: if n passes the test, repeat it for other values ato increase the confidence.

Part 2 of 3: How Simplicity Tests Work

1. 1 Enumeration of divisors. By definition, the number n is simple only if it is not divisible by 2 and other integers except 1 and itself. The above formula allows you to remove unnecessary steps and save time: for example, after checking if a number is divisible by 3, there is no need to check if it is divisible by 9.
   • The floor (x) function rounds x to the nearest integer less than or equal to x.
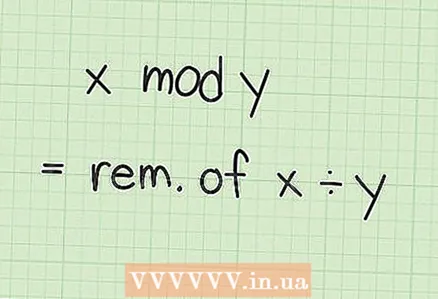2. 2 Learn about modular arithmetic. The operation "x mod y" (mod is an abbreviation of the Latin word "modulo", that is, "module") means "divide x by y and find the remainder." In other words, in modular arithmetic, upon reaching a certain value, which is called module, the numbers "turn" to zero again. For example, the clock counts down with module 12: it shows 10, 11 and 12 o'clock and then returns to 1.
   • Many calculators have a mod key. The end of this section shows you how to manually compute this function for large numbers.
3. 3 Learn about the pitfalls of Fermat's Little Theorem. All numbers for which the test conditions are not met are composite, but the rest of the numbers are only probably are simple. If you want to avoid incorrect results, search n in the list of "Carmichael numbers" (composite numbers that satisfy this test) and "Fermat pseudoprime numbers" (these numbers meet the test conditions only for some values a).
4. 4 If convenient, use the Miller-Rabin test. Although this method is rather cumbersome for manual calculations, it is often used in computer programs. It provides acceptable speed and fewer errors than Fermat's method. A composite number will not be taken as a prime number if calculations are performed for more than ¼ values a... If you randomly choose different values a and for all of them the test will give a positive result, we can assume with a fairly high degree of confidence that n is a prime number.
5. 5 For large numbers, use modular arithmetic. If you don't have a mod calculator handy, or the calculator isn't designed to handle such large numbers, use power properties and modular arithmetic to make the calculations easier. Below is an example for ${ displaystyle 3 ^ {50}}$ mod 50:
   • Rewrite the expression in a more convenient form: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Manual calculations may require further simplifications.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Here we took into account the property of modular multiplication.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Part 3 of 3: Using the Chinese Remainder Theorem

1. 1 Pick two numbers. One of the numbers must be composite, and the other must be exactly the one you want to test for simplicity.
   • Number1 = 35
   • Number2 = 97
2. 2 Select two values ​​that are greater than zero and, respectively, less than the numbers Number1 and Number2. These values ​​must not be the same.
   • Value1 = 1
   • Value2 = 2
3. 3 Calculate the MMI (Mathematical Multiplicative Inverse) for Number1 and Number2.
   • Calculate MMI
     • MMI1 = Number2 ^ -1 Mod Number1
     • MMI2 = Number1 ^ -1 Mod Number2
   • For prime numbers only (this will give a number for composite numbers, but it won't be his MMI):
     • MMI1 = (Number2 ^ (Number1-2))% Number1
     • MMI2 = (Number1 ^ (Number2-2))% Number2
   • For example:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Create a table for each MMI down to log2 modules:
   • For MMI1
     • F (1) = Number2% Number1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Number1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Number1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Number1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Number1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Number1 = 1 * 1% 35 = 1
   • Calculate Paired Numbers 1 - 2
     • 35 -2 = 33 (10001) base 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • For MMI2
     • F (1) = Number1% Number2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Number2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Number2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Number2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Number2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Number2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Number2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Number2 = 35 * 35 mod 97 = 61
   • Calculate the Paired Number 2 - 2
     • 97 - 2 = 95 = (1011111) base 2
     • MMI2 = (((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Calculate (Value1 * Number2 * MMI1 + Value2 * Number1 * MMI2)% (Number1 * Number2)
   • Answer = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Answer = (2619 + 4270)% 3395
   • Answer = 99
6. 6 Check that Number1 is not prime
   • Calculate (Answer - Value1)% Number1
   • 99 – 1 % 35 = 28
   • Since 28 is greater than 0, 35 is not a prime number.
7. 7 Check that Number2 is prime.
   • Calculate (Answer - Value2)% Number2
   • 99 – 2 % 97 = 0
   • Since 0 is 0, 97 is most likely a prime number.
8. 8 Repeat steps 1 through 7 at least two more times.
   • If you get 0 in step 7:
     • Use a different Number1 if Number1 is not prime.
     • Use another Number1 if Number1 is prime. In this case, you should get 0 in steps 6 and 7.
     • Use different Meaning1 and Meaning2.
   • If in step 7 you consistently get 0, then Number 2 is very likely to be prime.
   • Steps 1 through 7 may result in an error if Number1 is not prime and Number2 is a divisor of Number1. The described method works in all cases when both numbers are prime.
   • The reason you need to repeat steps 1 through 7 is because in some cases, even if Number1 and Number 2 are not prime, in step 7 you will get 0 (for one or both numbers). This rarely happens.Choose another Number1 (composite), and if Number2 is not prime, then Number2 will not equal zero in step 7 (unless Number1 is a divisor of Number2 - here primes will always equal zero in step 7).

Tips

• Prime numbers from 168 to 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Although brute force testing is a tedious test when dealing with large numbers, it is quite efficient for small numbers. Even in the case of large numbers, start by testing small divisors, and then move on to more sophisticated methods for checking the simplicity of numbers (if small divisors are not found).

What do you need

• Paper, pen or computer