Author:
Bobbie Johnson
Date Of Creation:
10 April 2021
Update Date:
26 June 2024
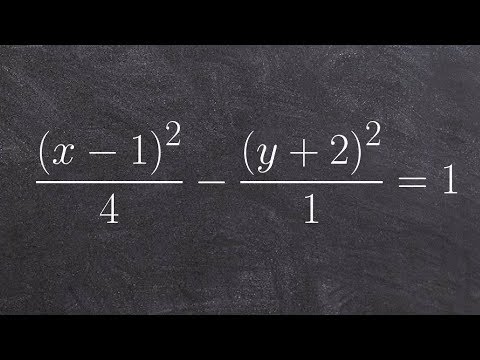
Content
Hyperbola asymptotes are straight lines passing through the center of the hyperbola. The hyperbola approaches the asymptotes, but never crosses (or even touches) them. There are two ways to find the equations of the asymptotes that will help you understand the very concept of asymptotes.
Steps
Method 1 of 2: Factoring
1 Write down the canonical hyperbole equation. Let's consider the simplest example - a hyperbola, the center of which is located at the origin. In this case, the canonical hyperbola equation has the form: /a - /b = 1 (when the branches of the hyperbola are directed to the right or left) or /b - /a = 1 (when the branches of the hyperbola are directed up or down). Keep in mind that in this equation, "x" and "y" are variables, and "a" and "b" are constants (that is, numbers). - Example 1:/9 - /16 = 1
- Some teachers and textbook authors swap the constant "a" and "b". Therefore, study the equation given to you to understand what's what. Do not just memorize the equation - in this case, you will not understand anything if variables and / or constants are denoted by other symbols.
2 Set the canonical equation to zero (not one). The new equation describes both asymptotes, but it takes some effort to get the equation for each asymptote. - Example 1:/9 - /16 = 0
3 Factor the new equation. Factor the left side of the equation. Remember how to factor a quadratic equation, and read on. - The final equation (that is, the factorized equation) will be (__ ± __) (__ ± __) = 0.
- When multiplying the first terms (inside each pair of parentheses), you should get the term /9, so extract the square root from this member, and write the result instead of the first space inside each pair of parentheses: (/3 ± __)(/3 ± __) = 0
- Similarly, extract the square root of the term /16, and write the result instead of the second space inside each pair of parentheses: (/3 ± /4)(/3 ± /4) = 0
- You have found all the terms of the equation, so inside one pair of parentheses between the terms write a plus sign, and inside the second - a minus sign, so that when multiplying, the corresponding terms are canceled: (/3 + /4)(/3 - /4) = 0
4 Set each binomial (that is, the expression within each pair of parentheses) to zero and compute "y". This will find two equations that describe each asymptote. - Example 1: As (/3 + /4)(/3 - /4) = 0, then /3 + /4 = 0 and /3 - /4 = 0
- Rewrite the equation as follows: /3 + /4 = 0 → /4 = - /3 → y = - /3
- Rewrite the equation as follows: /3 - /4 = 0 → - /4 = - /3 → y = /3
5 Follow the described steps with a hyperbola whose equation differs from the canonical one. In the previous step, you found the equations for the asymptotes of the hyperbola centered at the origin. If the center of the hyperbola is at a point with coordinates (h, k), then it is described by the following equation: /a - /b = 1 or /b - /a = 1. This equation can also be factorized. But in this case, do not touch the binomials (x - h) and (y - k) until you come to the last step. - Example 2: /4 - /25 = 1
- Set this equation to 0 and factor it:
- (/2 + /5)(/2 - /5) = 0
- Equate each binomial (that is, the expression inside each pair of parentheses) to zero and calculate "y" to find the equations for the asymptotes:
- /2 + /5 = 0 → y = - /2x + /2
- (/2 - /5) = 0 → y = /2x - /2
Method 2 of 2: Calculate Y
1 Isolate the y term on the left side of the hyperbola equation. Use this method when the hyperbola equation is in quadratic form. Even if a canonical hyperbola equation is given, this method will allow a better understanding of the concept of asymptotes. Insulate y or (y - k) on the left side of the equation. - Example 3:/16 - /4 = 1
- Add x to both sides of the equation, and then multiply both sides by 16:
- (y + 2) = 16 (1 + /4)
- Simplify the resulting equation:
- (y + 2) = 16 + 4 (x + 3)
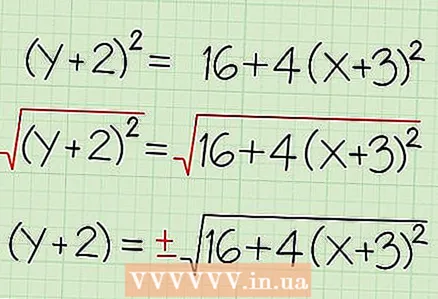2 Take the square root of each side of the equation. However, do not oversimplify the right side of the equation, since when you extract the square root, you get two results - positive and negative (for example, -2 * -2 = 4, so √4 = 2 and √4 = -2). To list both results, use the ± symbol. - √ ((y + 2)) = √ (16 + 4 (x + 3))
- (y + 2) = ± √ (16 + 4 (x + 3))
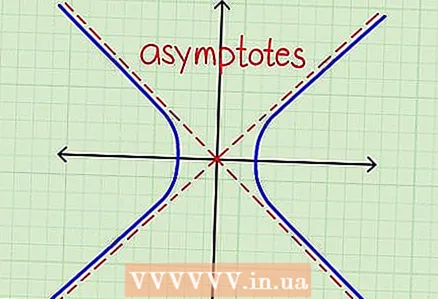3 Understand the concept of asymptotes. Do this before moving on to the next step. An asymptote is a straight line, to which the hyperbola approaches with increasing values of "x".The hyperbola will never cross the asymptote, but with increasing "x" the hyperbola will approach the asymptote at an infinitely small distance. 
4 Transform the equation to account for large x values. As a rule, when working with the equations of asymptotes, only large values of "x" are taken into account (that is, those values that tend to infinity). Therefore, certain constants can be neglected in the equation, since their contribution is small compared to "x". For example, if the variable "x" is equal to several billion, then adding the number (constant) 3 will have a negligible effect on the value of "x". - In the equation (y + 2) = ± √ (16 + 4 (x + 3)) as “x” tends to infinity, the constant 16 can be neglected.
- For large values of "x" (y + 2) ≈ ± √ (4 (x + 3))
5 Calculate y to find the equations for the asymptotes. By getting rid of the constants, you can simplify the radical expression. Remember that you need to write two equations in your answer - one with a plus sign and the other with a minus sign. - y + 2 = ± √ (4 (x + 3) ^ 2)
- y + 2 = ± 2 (x + 3)
- y + 2 = 2x + 6 and y + 2 = -2x - 6
- y = 2x + 4andy = -2x - 8
Tips
- Remember that the equation of the hyperbola and the equations of its asymptotes always include constants (constants).
- An equilateral hyperbola is a hyperbola in the equation of which a = b = c (constant).
- If given an equilateral hyperbola equation, first convert it to canonical form and then find the equations for the asymptotes.
Warnings
- Remember that the answer is not always written in canonical form.
