How to divide matrices

Video: Algebra II 13.6C, Dividing matrices by using inverses

Content

Brief summary
Steps
Part 1 of 3: Testing the Divisibility of Matrices
Part 2 of 3: Finding the Inverse Matrix
Part 3 of 3: Matrix multiplication
Tips
Warnings
Additional articles

If you know how to multiply two matrices, you can start “dividing” the matrices. The word “division” is enclosed in quotation marks, because matrices cannot actually be divided. The division operation is replaced by the operation of multiplying one matrix by a matrix that is the inverse of the second matrix. For simplicity, consider an example with integers: 10 ÷ 5. Find the reciprocal of 5: 5 or /₅, and then replace division by multiplication: 10 x 5; the result of division and multiplication will be the same. Therefore, it is believed that division can be replaced by multiplication by the inverse matrix. Typically, such calculations are used to solve systems of linear equations.

Brief summary

You cannot divide matrices. Instead of dividing, one matrix is multiplied by the inverse of the second matrix. "Division" of two matrices [A] ÷ [B] is written as follows: [A] * [B] or [B] * [A].
If matrix [B] is not square, or if its determinant is 0, write down "no unambiguous solution." Otherwise, find the determinant of the matrix [B] and go to the next step.
Find the inverse: [B].
Multiply matrices to find [A] * [B] or [B] * [A]. Keep in mind that the order in which the matrices are multiplied affects the final result (that is, the results may vary).

Steps

Part 1 of 3: Testing the Divisibility of Matrices

1 Understand the "division" of matrices. In fact, matrices cannot be divided. There is no such mathematical operation as “dividing one matrix by another”. Division is replaced by multiplying one matrix by the inverse of the second matrix. That is, the notation [A] ÷ [B] is not correct, so it is replaced with the following notation: [A] * [B]. Since both entries are equivalent in the case of scalar values, theoretically we can talk about "division" of matrices, but it is still better to use the correct terminology.
- Note that [A] * [B] and [B] * [A] are different operations. It may be necessary to perform both operations to find all possible solutions.
- For example, instead of ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} div { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ write down ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1}}$ .
  You may have to compute ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}}}$ to get a different result.
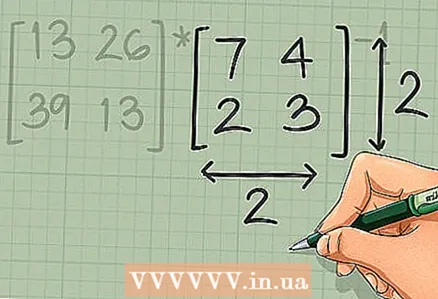2 Make sure the matrix you are “dividing” the other matrix by is square. To invert a matrix (find the inverse of a matrix), it must be square, that is, with the same number of rows and columns. If the inverted matrix is not inverse, there is no definite solution.
- Again, the matrices are not "divisible" here. In operation [A] * [B], the described condition refers to the matrix [B]. In our example, this condition refers to the matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$
- A matrix that can be inverted is called non-degenerate or regular. A matrix that cannot be inverted is called degenerate or singular.
3 Check if the two matrices can be multiplied. To multiply two matrices, the number of columns in the first matrix must be equal to the number of rows in the second matrix. If this condition is not met in the entry [A] * [B] or [B] * [A], there is no solution.
- For example, if the size of the matrix [A] is 4 x 3 and the size of the matrix [B] is 2 x 2, there is no solution. You cannot multiply [A] * [B], because 4 ≠ 2, and you cannot multiply [B] * [A], since 2 ≠ 3.
- Note that the inverse matrix [B] always has the same number of rows and columns as the original matrix [B]. It is not necessary to find the inverse matrix to check that two matrices can be multiplied.
- In our example, the size of both matrices is 2 x 2, so they can be multiplied in any order.
4 Find the determinant of the 2 × 2 matrix. Remember: you can invert a matrix only if its determinant is not zero (otherwise, you cannot invert the matrix). Here's how to find the determinant of a 2 x 2 matrix:
- 2 x 2 Matrix: determinant of a matrix ${ displaystyle { begin {pmatrix} a & b c & d end {pmatrix}}}$ is equal to ad - bc. That is, from the product of the elements of the main diagonal (passes through the upper left and lower right corners), subtract the products of the elements of the other diagonal (passes through the upper right and lower left corners).
- For example, the determinant of the matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ is equal to (7) (3) - (4) (2) = 21 - 8 = 13. The determinant is nonzero, so this matrix can be inverted.
5 Find the determinant of the larger matrix. If the size of the matrix is 3 x 3 or more, the determinant is slightly more difficult to compute.
- 3 x 3 matrix: select any item and cross out the row and column it is in.Find the determinant of the resulting 2 × 2 matrix, and then multiply it by the selected element; specify the sign of the determinant in a special table. Repeat this process for the other two items that are in the same row or column as the item you selected. Then find the sum of the (three) determinants received. Read this article for more information on how to find the determinant of a 3 x 3 matrix.
- Large matrices: the determinant of such matrices is best sought with a graphing calculator or software. The method is similar to the method for finding the determinant of a 3 × 3 matrix, but it is rather tedious to apply it manually. For example, to find the determinant of a 4 x 4 matrix, you need to find the determinants of four 3 x 3 matrices.
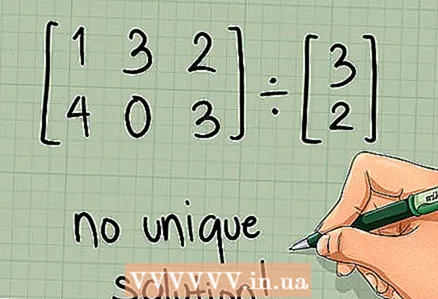6 Continue calculations. If the matrix is not square or if its determinant is equal to zero, write "no unambiguous solution", that is, the calculation process is completed. If the matrix is square and has a nonzero determinant, skip to the next section.

Part 2 of 3: Finding the Inverse Matrix

1 Swap the elements of the main diagonal of the 2 x 2 matrix. Given a 2 × 2 matrix, use the quick inverse method. First, swap the top-left element and the bottom-right element. For example:
- ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$
- Note: most people use calculators to invert a 3 x 3 (or larger) matrix. If you need to do this manually, go to the end of this section.
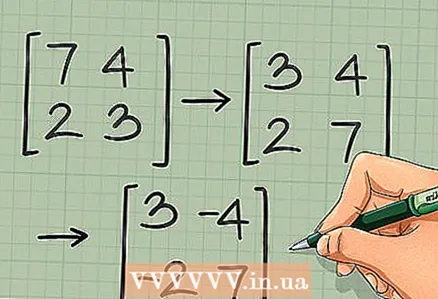2 Do not swap the remaining two elements, but change their sign. That is, multiply the top-right element and the bottom-left element by -1:
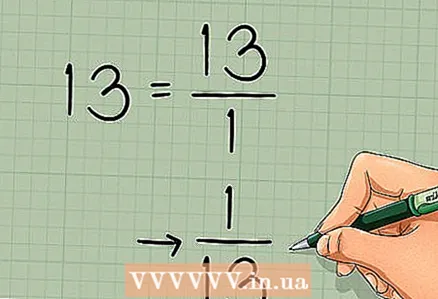- ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
3 Find the reciprocal of the determinant. The determinant of this matrix was found in the previous section, so we will not calculate it again. The inverse of the determinant is written as follows: 1 / (determinant):
- In our example, the determinant is 13. Reverse value: ${ displaystyle { frac {1} {13}}}$ .
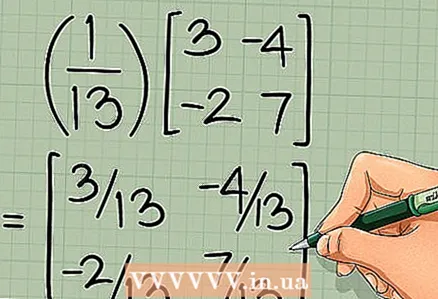4 Multiply the resulting matrix by the reciprocal of the determinant. Multiply each element of the new matrix by the inverse of the determinant. The final matrix will be the inverse of the original 2 x 2 matrix:
- ${ displaystyle { frac {1} {13}} * { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
  = ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$
5 Check if the calculations are correct. To do this, multiply the original matrix by its inverse. If the calculations are correct, the product of the original matrix by the inverse will give the identity matrix: (1001){ displaystyle { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}... If the test was successful, proceed to the next section.
- In our example: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} = { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}$ .
- For more information on how to multiply matrices, read this article.
- Note: the operation of matrix multiplication is not commutative, that is, the order of the matrices is important. But when the original matrix is multiplied by its inverse, any order leads to the identity matrix.
6 Find the inverse of a 3 x 3 matrix (or larger). If you are already familiar with this process, it is better to use a graphing calculator or dedicated software. If you need to find the inverse matrix manually, the process is briefly described below:
- Join the identity matrix I on the right side of the original matrix. For example, [B] → [B | I]. For the identity matrix, all elements of the main diagonal are equal to 1, and all other elements are equal to 0.
- Simplify the matrix so that its left side is stepped; continue simplifying so that the left side becomes the identity matrix.
- After simplification, the matrix will take the following form: [I | B]. That is, its right side is the inverse of the original matrix.

Part 3 of 3: Matrix multiplication

1 Write down two possible expressions. The operation of multiplying two scalars is commutative, that is, 2 x 6 = 6 x 2.This is not the case in the case of matrix multiplication, so you may have to solve two expressions:
- x = [A] * [B] is the solution to the equation x[B] = [A].
- x = [B] * [A] is a solution to equation [B]x = [A].
- Perform each math operation on both sides of the equation. If [A] = [C] then [B] [A] ≠ [C] [B] because [B] is to the left of [A] but to the right of [C].
2 Determine the size of the final matrix. The size of the final matrix depends on the size of the multiplied matrices. The number of rows in the final matrix is equal to the number of rows in the first matrix, and the number of columns in the final matrix is equal to the number of columns in the second matrix.
- In our example, the size of both matrices ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}}}$ and ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$ is 2 x 2, so the size of the original matrix will be 2 x 2.
- Consider a more complex example: if the size of the matrix [A] is 4 x 3, and the size of the matrix [B] is 3 x 3, then the final matrix [A] * [B] will be 4 x 3.
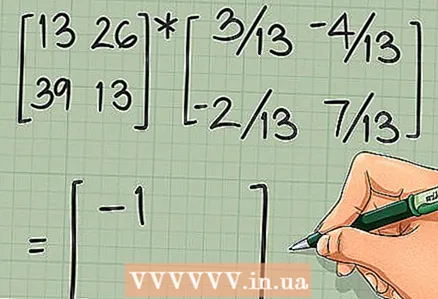3 Find the value of the first element. Read this article or remember the following basic steps:
- To find the first element (first row, first column) of the final matrix [A] [B], calculate the dot product of the elements of the first row of matrix [A] and the elements of the first column of matrix [B]. In the case of a 2 x 2 matrix, the dot product is calculated as follows: ${ displaystyle a_ {1,1} * b_ {1,1} + a_ {1,2} * b_ {2,1}}$ .
- In our example: ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}}}$ ... Thus, the first element of the final matrix will be the element:
  ${ displaystyle (13 * { frac {3} {13}}) + (26 * { frac {-2} {13}})}$
  ${ displaystyle = 3 + -4}$
  ${ displaystyle = -1}$
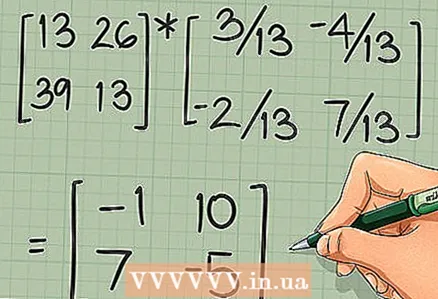4 Continue calculating dot products to find each element of the final matrix. For example, the element located in the second row and the first column is equal to the dot product of the second row of the matrix [A] and the first column of the matrix [B]. Try to find the remaining items yourself. You should get the following results:
- ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}} = { begin {pmatrix} -1 & 10 7 & -5 end {pmatrix}}}$
- If you need to find another solution: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} = { begin {pmatrix} -9 & 2 19 & 3 end {pmatrix}}}$

Tips

The matrix can be divided into a scalar; for this, each element of the matrix is divided by a scalar.
- For example, if the matrix ${ displaystyle { begin {pmatrix} 6 & 8 2 & 4 end {pmatrix}}}$ divided by 2, you get the matrix ${ displaystyle { begin {pmatrix} 3 & 4 1 & 2 end {pmatrix}}}$

Warnings

The calculator does not always give absolutely accurate results when it comes to matrix calculations. For example, if the calculator claims that the item is a very small number (such as 2E), the value is most likely zero.