Content

• Steps
• Advice
• Warning

Hypothesis testing is guided by statistical analysis. Statistically significant confidence is calculated using p value - which indicates the probability of an observed result when a certain (zero hypothesis) is true. If the p-value is less than the significance level (usually 0.05), the experimenter can conclude that there is enough evidence to disprove the null hypothesis and admit the inverse hypothesis. Using a simple t-test, you can calculate the p-value and determine the significance between two different groups of data.

Steps

Part 1 of 3: Set up your experiments

1. 

   Determine your hypothesis. The first step in evaluating statistical significance is identifying the questions to answer and declaring your hypothesis. Hypothesis is a statement of the empirical data and possible discrepancies in the population. Every experiment has a null hypothesis and an inverse hypothesis. In general, you will compare two groups to see if they are the same or different.
   • In general, hypothesis is not (H₀) confirm that there is no difference between the two groups of data. Example: Students who read the material before class do not get better final grades.
   • The inverse hypothesis (H_a) is contrary to the null hypothesis and is a statement that you are trying to support with your empirical data. Example: Students who read the material before class actually get better final grades.

2. 

   
   
   Select the significance level to determine the degree of difference that can be seen as meaningful in the data. Significance level (also known as alpha) is the threshold you choose to determine meaning. If the p value is less than or equal to a given significance level, the data is considered statistically significant.
   • As a general rule, the significance level (or alpha) is usually chosen at the 0.05 level - meaning that the probability of observing the difference seen on the data is random only 5%.
   • The higher the confidence level (and therefore, the lower the p-value), the more meaningful the results.
   • If more confidence is required, lower the p-value to 0.01. A low p-value is often used in manufacturing to detect product defects. A high degree of reliability is critical to accept that every part will function as it should be.
   • For most hypothesis-based experiments, a significance level of 0.05 is acceptable.

3. 

   
   
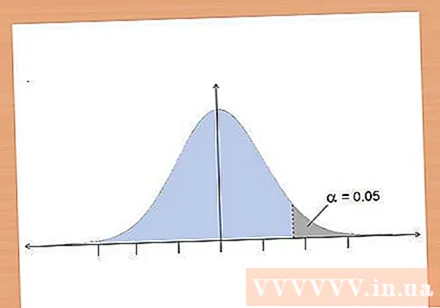
   Decide whether to use a one-tailed or two-tailed test. One of the t-test assumptions is that your data is in a normal distribution. The normal distribution will form a bell curve with the majority of the observations centered. The t-test is a mathematical test that checks whether your data falls on the outside of the normal distribution, above or below, in the “top” part of the curve.
   • If you are not sure whether the data is above or below the control group, use a two-tailed test. It allows you to check significance in both directions.
   • If you know what the expected direction of your data is, use a one-tailed test. In the example above, you expect that the student's scores will improve. Therefore, you use the one-tailed test.

4. 

   
   
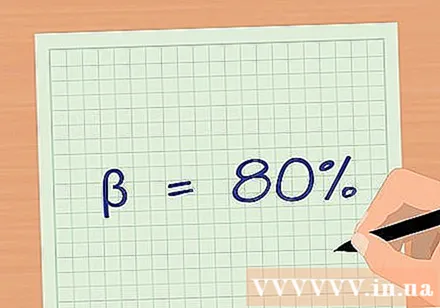
   Determine sample size with force analysis. The force of a test is the ability to observe the expected result with a given sample size. The common threshold for force (or β) is 80%. Force analysis can be quite complicated without some preliminary data because you need some information about the expected mean between the groups and their standard deviations. Use online force analysis to determine the optimal sample size for your data.
   • Researchers often perform a small premise study to inform the force analysis and decide the sample size needed for a large and comprehensive study.
   • If there is no means to do complex premise research, estimate the possible mean based on reading articles and research that other individuals may have done. It can give you a good start in determining sample sizes.
   advertisement

Part 2 of 3: Calculate the standard deviation

1. 

   Determine the formula for standard deviation. Standard deviation measures the dispersion of the data. It gives you information about the identity of each data point in the sample. When first getting started, equations can look quite complicated. However, the steps below will help you to easily understand the calculation process. The formula is s = √∑ ((x_i - µ) / (N - 1)).
   • s is the standard deviation.
   • ∑ indicates that you will have to add up all the observations collected.
   • x_i each represents your data value.
   • µ is the mean of the data for each group.
   • N is the total number of observations.

2. 

   Averaged the observed data for each group. To calculate the standard deviation, you first need to calculate the mean of the observations for each individual group. This value is symbolized with the Greek letter mu or µ. To do that, simply add the observations and divide by the total number of observations.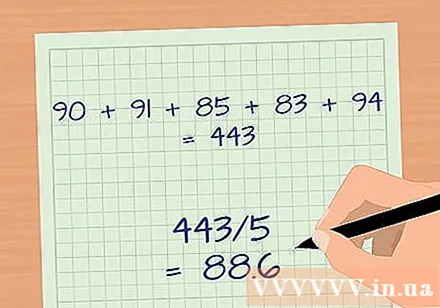
   • For example, to find the average score of the group reading the document before class, let's look at some data. For simplicity, we will use a data set of 5 points: 90, 91, 85, 83 and 94 (on a 100-point scale).
   • Add up all observations: 90 + 91 + 85 + 83 + 94 = 443.
   • Divide the sum above by the number of observations N (N = 5): 443/5 = 88.6.
   • The average score for this group is 88.6.

3. 

   Subtract the average from each observed value. The next step involves part (x_i - µ) of the equation. Subtract the average value from each observed value. With the above example, we have five subtractions.
   • (90 - 88.6), (91- 88.6), (85 - 88.6), (83 - 88.6) and (94 - 88.6).
   • The calculated value is 1.4; 2.4; -3.6; -5.6 and 5.4.

4. 

   Square the above differences and add them up. Each new value just calculated will now be squared. Here, the negative sign will also be removed. If a negative sign appears after this step or at the end of the calculation, you may have forgotten to do the above step.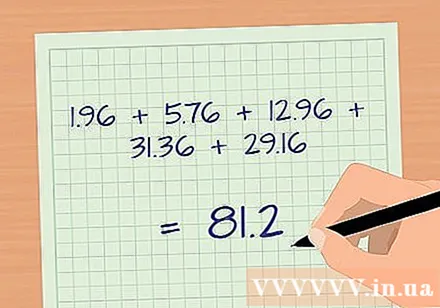
   • In our example, we will now work with 1.96; 5.76; 12.96; 31.36 and 29.16.
   • Add these squares together: 1.96 + 5.76 + 12.96 + 31.36 + 29.16 = 81.2.

5. 

   Divide by the total number of observations minus 1. Dividing by N - 1 helps to compensate for a calculation that is not performed on the population as a whole, but is based on a sample of all students.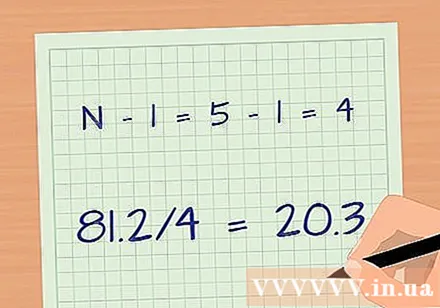
   • Subtract: N - 1 = 5 - 1 = 4
   • Divide: 81.2 / 4 = 20.3

6. 

   Get the square root. Once divided by the number of observations minus 1, take the square root of the value obtained. This is the last step in calculating the standard deviation. Some statistical programs will help you perform this calculation after the original data is imported.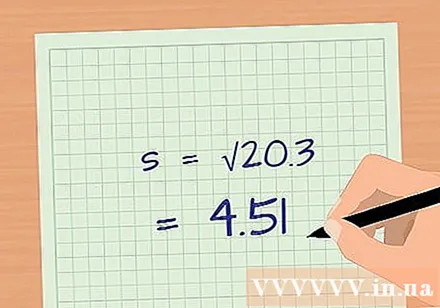
   • With the above example, the standard deviation of the end-of-semester grade of students reading the document before class is: s = √20,3 = 4.51.
   advertisement

Part 3 of 3: Determination of statistical significance

1. 

   Calculate the variance between your two groups of observations. Up to this point, the example has only dealt with one group of observations. To compare two groups, you obviously need data from both. Calculate the standard deviation of the second group of observations and use it to calculate the variance between the two experimental groups. The formula for calculating variance is: s_d = √ ((s₁/ N₁) + (s₂/ N₂)).
   • S_d is the variance between the groups.
   • S₁ is the standard deviation of groups 1 and N₁ is the size of group 1.
   • S₂ is the standard deviation of groups 2 and N₂ is the size of group 2.
   • In our example, let's say that the data from group 2 (students who did not read the text before class) has a size of 5 and a standard deviation of 5.81. The variance is:
     • S_d = √ ((s₁) / N₁) + ((s₂) / N₂))
     • S_d = √(((4.51)/5) + ((5.81)/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6.75) = √10.82 = 3.29.

2. 

   Calculate the t-score of the data. T-statistics allow you to convert data into a form that is comparable to other data. The t-value also allows you to perform a t-test, a test that allows you to calculate the likelihood of a statistically significant difference between the two groups. The formula for calculating the t-statistic is: t = (µ₁ – µ₂)/S_d.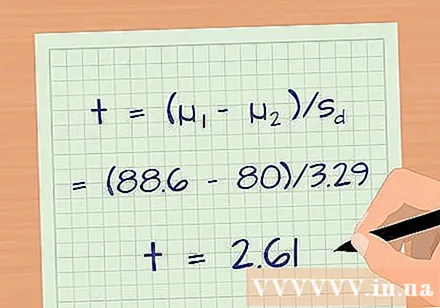
   • µ₁ is the average of the first group.
   • µ₂ is the average of the second group.
   • S_d is the variance between the observations.
   • Use the larger mean as µ₁ in order not to get a negative t-statistic.
   • For our example, suppose the observed mean for group 2 (who did not read the previous article) is 80. The t-score is: t = (µ₁ – µ₂)/S_d = (88,6 – 80)/3,29 = 2,61.

3. 

   Determine the degree of freedom of the sample. When using the t-statistic, the degrees of freedom are determined based on the sample size. Add up the number of observations for each group and then subtract two. In the above example, the degree of freedom (d.f.) is 8 because there are 5 samples in the first group and 5 samples in the second group ((5 + 5) - 2 = 8).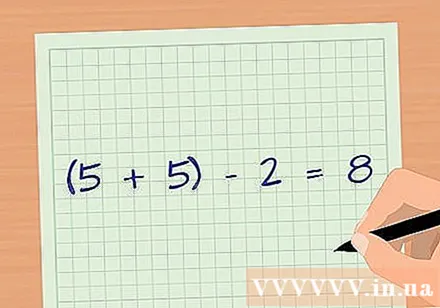

4. 

   Use table t to evaluate significance. Tables of t-values ​​and degrees of freedom can be found in a standard statistics book or online. Find the row that contains the degrees of freedom of the data and the p-value that corresponds to the t-statistic you have.
   • With degrees of freedom 8 and t = 2.61, the p-value for a one-tailed test lies between 0.01 and 0.025. Since the significance level chosen is less than or equal to 0.05, our data is statistically significant. With this data, we reject the null hypothesis and accept the inverse hypothesis: students who read the material before class have higher final grades.

5. 

   Consider conducting further research. Many researchers perform premise studies with several metrics to understand how to design a larger study. Doing other research with more metrics will increase your confidence in your conclusions. advertisement

Advice

• Statistics is a large and complex field. Take a high school or university (or higher) statistical hypothesis testing course to understand statistical significance.

Warning

• This analysis focuses on the t-test to check the difference between the two normal distribution populations. Depending on the complexity of the data, you may need another statistical test.