Content

• To step
• Part 1 of 5: Calculating the resulting displacement
• Part 2 of 5: If the velocity vector and time duration are known
• Part 3 of 5: When the speed, acceleration and time are given
• Part 4 of 5: Calculating the angular displacement
• Part 5 of 5: Understanding displacement
• Tips
• Necessities

The term displacement in physics refers to the change in place of an object. When calculating the displacement, you measure how much an object has moved based on the data from the start position and the end position. The formula you use to determine the displacement depends on the variables given in an exercise. Take the following steps to learn how to calculate the displacement of an object.

To step

Part 1 of 5: Calculating the resulting displacement

1. Use the formula for the resulting displacement using the unit of length used to specify the start and end position. While distance is different from displacement, a resultant displacement statement will indicate how many "meters" an object has traveled. Use these units of measurement to calculate the displacement, how far an object is from its original location.
   • The equation for the resulting displacement is: s = √x² + y². "S" stands for displacement. X is the first direction in which the object is moving and y is the second direction in which the object is moving. If your object only moves in 1 direction, then y = 0.
   • An object can only move in maximum 2 directions, because moving along the north-south line or the east-west line is considered a neutral movement.
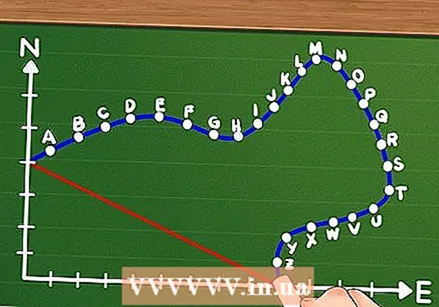2. Connect the points according to the order of movement and label these points from A-Z. Use a ruler to draw straight lines from point to point.
   • Also don't forget to connect the starting point with the end point, using a straight line. This is the displacement we are going to calculate.
   • For example, if an object travels first 300 meters east and then 400 meters north, a right triangle is formed. AB is the first side and BC the second side of the triangle. AC is the triangle's hypotenuse, and its value is the object's displacement. In this example, the two directions are "east" and "north."
3. Enter the values ​​for x² and y². Now that you know the direction in which your object is moving, you can enter the values ​​for the relevant variables.
   • For example, x = 300 and y = 400. Your equation now looks like this: s = √300² + 400².
4. Work out the equation. First calculate 300² and then 400², add them together and subtract the square root of the sum.
   • For example: s = √90000 + 160000. s = √250000. s = 500. You now know that the displacement is equal to 500 meters.

Part 2 of 5: If the velocity vector and time duration are known

1. Use this formula if the problem gives the velocity vector and the duration. It may happen that a physics task does not mention the distance traveled, but it does state how long an object has been in transit and at what speed. You can then calculate the displacement using the duration and the speed.
   • In this case, the equation will look like this: s = 1/2 (u + v) t. u = the initial speed of the object, the speed at which the object started to move in a certain direction. v = the final speed of the object, or how fast it went at the end. t = the amount of time it took for the object to reach its destination.
   • For example: A car runs for 45 seconds. The car turned west at a speed of 20 m / s (initial speed) and at the end of the street the speed is 23 m / s (final speed). Calculated the displacement based on this data.
2. Enter the values ​​for the speed and time. Now that you know how long the car has been running, and what the initial speed and final speed were, you can find the distance from the start point to the end point.
   • The equation will look like this: s = 1/2 (20 + 23) 45.
3. Evaluate the equation when you have entered the values. Remember to calculate the terms in the correct order, otherwise the displacement will go wrong.
   • For this comparison, it doesn't matter much if you accidentally switch the start and end speeds. Because you add these values ​​together first, this does not matter. But with other equations, swapping the start and end speeds can affect the final answer, or the value of the displacement.
   • Your equation now looks like this: s = 1/2 (43) 45. First, divide 43 by 2 to give 21.5 as the answer. Multiply 21.5 by 45, which gives the answer 967.5 meters. 967.5 is the displacement of the car as seen from the starting point.

Part 3 of 5: When the speed, acceleration and time are given

1. Another comparison is necessary if the acceleration is given, together with the speed and the time. With such an assignment you know what the initial speed of the object was, what the acceleration is and how long the object has been on the road. You need the following equation.
   • The equation for this type of problem looks like this: s = ut + 1 / 2at². The "u" still represents the initial speed; The "a" is the acceleration of the object, or how fast the speed of the object changes. The variable "t" can either mean the total duration of time, or it can indicate a specific period in which the object has accelerated. Either way, this is indicated in time units such as seconds, hours, etc.
   • Suppose a car with an initial speed of 25 m / s accelerates at 3 m / s2 for a period of 4 seconds. What is the displacement of the car after 4 seconds?
2. Enter the values ​​in the correct place in the equation. Unlike the previous equation, only the initial speed is shown here, so make sure to enter the correct values.
   • Based on the example above, your equation should now look like this: s = 25 (4) + 1/2 (3) 4². It can certainly help if you put parentheses around the acceleration and time values ​​to keep the numbers separate.
3. Calculate the displacement by solving the equation. A quick way to help you remember the order of operations in an equation is the mnemonic "Mr. van Dale Waiting For Answer". Indicates all arithmetic operations in sequence (Exponentiation, Multiplication, Division, Square root, Addition, and Subtraction).
   • Let's take a closer look at the equation: s = 25 (4) + 1/2 (3) 4². The order is: 4² = 16; then 16 x 3 = 48; then 25 x 4 = 100; and if last 48/2 = 24. The equation now looks like this: s = 100 + 24. After adding this gives s = 124, the displacement is 124 meters.

Part 4 of 5: Calculating the angular displacement

1. Determining the angular displacement when an object moves along a curve. Although you will still calculate the displacement using a straight line, you will need the difference between the start and end positions along a curved path.
   • Take a girl riding a merry-go-round as an example. As she spins around the outside of the wheel, she moves in a circle. Angular displacement tries to find the shortest distance between start and end position when an object is not moving in a straight line.
   • The angular displacement formula is: θ = S / r, where "s" is the linear displacement, "r" is the radius, and "θ" is the angular displacement. Linear displacement is the distance an object travels along a circle. The radius or radius is the distance of an object from the center of the circle. Angular displacement is value we want to know.
2. Enter the values ​​of the linear displacement and the radius in the equation. Remember that radius is the distance from the center of a circle to the edge; it may be that the diameter is given in an exercise, in which case you will have to divide it by 2 to find the radius (radius) of the circle.
   • An example of an exercise: A girl is on a merry-go-round. Her chair is at a distance of 1 meter from the center of the circle (the radius). If the girl moves along a 1.5 meter circular arc (linear displacement), what is her angular displacement?
   • The equation looks like this: θ = 1.5 / 1.
3. Divide the linear displacement by the radius. This will give you the angular displacement of the object.
   • After the division 1.5 / 1 you are left with 1.5. The girl's angular displacement is 1.5 radians.
   • Because angular displacement indicates how much an object has rotated from its initial position, it is necessary to represent this in radians, not as a distance. Radians are units used to measure angles.

Part 5 of 5: Understanding displacement

1. It is important to understand that sometimes "distance" means something different than "displacement.“Distance says something about how far an object has moved in total.
   • Distance is something we also call a "scalar quantity". It is a way of indicating how much distance you have traveled, but it does not say anything about the direction you have moved.
   • For example, if you walk 2 meters east, 2 meters south, 2 meters west, and 2 meters north again, you are back at your starting point. Although you covered a total distance of 10 meters, your displacement equals 0 meters because your end point is the same as your starting point.
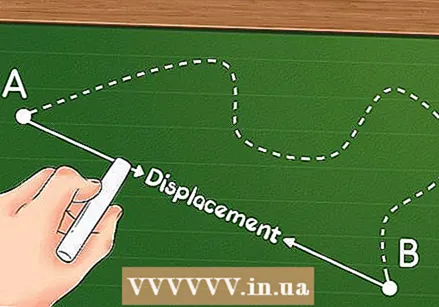2. Displacement is the difference between two points. Displacement is not the sum of movements as is the case with distance; it is only about the part between your start and your end point.
   • Displacement is also referred to as a "vector quantity" and refers to the change in the position of an object compared to the direction in which the object is moving.
   • Imagine you are walking 5 meters to the east. If you walk 5 meters west again, you will move in the opposite direction, back to your starting point. Even though you have walked a total of 10 meters, your position has not changed and your displacement is 0 meters.
3. Make sure to remember the words "back and forth" when trying to imagine a move. The opposite direction will undo the movement in the original direction.
   • Imagine a soccer coach bouncing back and forth along the sidelines. While giving directions to the players, he walked along the line several times, back and forth. If you were to keep an eye on the coach, you would see the distance he is traveling. But what if the coach stops to say something to a defender? If he is in a place different from his starting point, you look at the movement of the coach (at a certain moment).
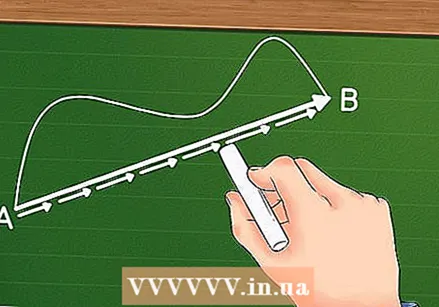4. Displacement is measured using a straight line, not a circular path. To find out the displacement, look for the shortest path between two different points.
   • A curved path will eventually lead you from start point to end point, but this is not the shortest way. To help you envision this, imagine walking in a straight line and being held back by a pillar or other obstacle. You cannot walk through the pillar, so go around it. Even though you end up in the same place as if you would have gone straight through the pillar, you still had to travel a longer way to get there.
   • Although displacement is preferably in a straight line, it is possible to measure the displacement of an object that "does" move along a curved path. This is called the "angular displacement" and it can be calculated by finding the shortest distance that exists between start point and end point.
5. Understand that displacement can also have a negative value, as opposed to distance. If the end point is reached by moving in a direction opposite to the direction you took off (relative to the start point), then your displacement is negative.
   • For example, suppose you walk 5 meters east and then 3 meters west. Although you are technically 2 meters away from your starting point, the displacement is -2 because you are moving in the opposite direction at that point. The distance will always be positive, because you cannot "undo" a distance you have traveled.
   • Negative displacement does not mean displacement decreases. It is simply a way of indicating that the movement is happening in the opposite direction.
6. Realize that the distance and displacement values ​​can sometimes be the same. If you walk straight for 25 meters and then stop, the distance you traveled is equal to the displacement, simply because you did not change direction.
   • This is only possible if you move in a straight line from the starting point, and without changing direction afterwards. For example, suppose you live in San Francisco, California and get a job in Las Vegas, Nevada. You will then have to move to Las Vegas to live closer to work. If you take the plane, a direct flight from San Francisco to Las Vegas, you have covered 670 km and your displacement is 670 km.
   • However, if you travel by car from San Francisco to Las Vegas, your journey may still be 670 km but you have covered 906 km in the meantime. Since driving usually involves a change of direction (turning, taking another route), you have traveled a much greater distance than the shortest distance between the two cities.

Tips

• Work accurately
• Do not memorize the formulas, but try to understand how they work

Necessities

• Calculator
• Rangefinder