Content

• To step
• Method 1 of 5: Calculating the volume of a triangular prism
• Method 2 of 5: Calculate the volume of a cube
• Method 3 of 5: Calculate the volume of a rectangular prism
• Method 4 of 5: Calculate the volume of a trapezoidal prism
• Method 5 of 5: Calculate the volume of a regular pentagonal prism
• Tips

A prism is a geometric figure with two identical ends and flat sides. The prism is named for the shape of its base, so a prism with a triangular base is called a "triangular prism." To calculate the volume of a prism, you just need to calculate the area of ​​the base and multiply it by the height - calculating the area of ​​the base can be the tricky part. Here you can read how to calculate the volume of various prisms.

To step

Method 1 of 5: Calculating the volume of a triangular prism

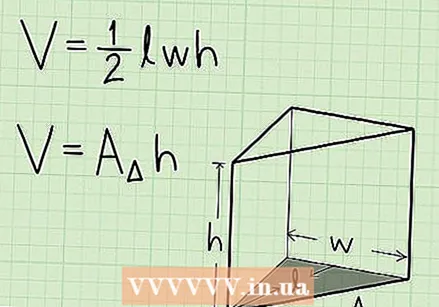1. Write down the formula for finding the volume of a triangular prism. The formula is V = 1/2 x length x width x height. But, we break this formula down further to get the formula V = area or base x height to use. You can calculate the area of ​​the base, using the formula for finding the area of ​​a triangle - multiply 1/2 by the length and width of the base.
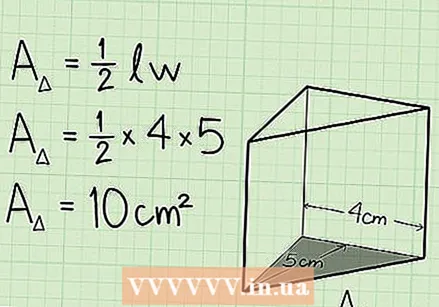2. Determine the area of ​​the base plane. To find the volume of a triangular prism, you will first need to determine the area of ​​the triangular base. Find the area of ​​the base of the prism by multiplying 1/2 times the base of the triangle times the height.
   • Ex: if the height of the triangular base is 5 cm and the base of the triangular prism is 4 cm, then the area of ​​the base is 1/2 x 5 cm x 4 cm, equal to 10 cm.
3. Determine the height. Suppose the height of this triangular prism is 7 cm.
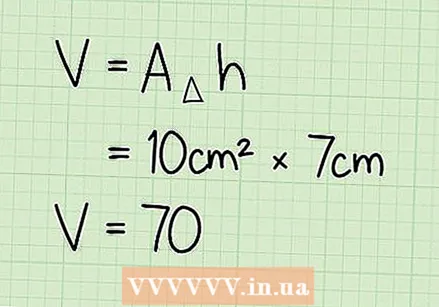4. Multiply the area of ​​the triangular base times the height. Multiply the area of ​​the base times the height. Multiply the base by the height, and you get the volume of the triangular prism.
   • Ex: 10 cm x 7 cm = 70 cm
5. Give your answer in cubic units. You should always use cubic units when calculating a volume, because you are working with three-dimensional objects. The final answer is 70 cm.

Method 2 of 5: Calculate the volume of a cube

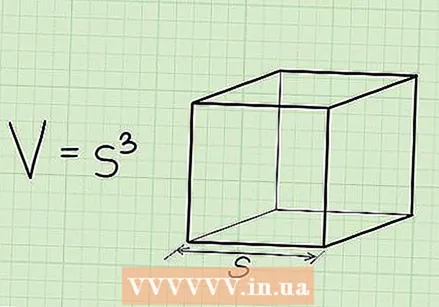1. Write the formula for finding the volume of a cube. The formula is V = silk. A cube is a prism with 3 equal sides.
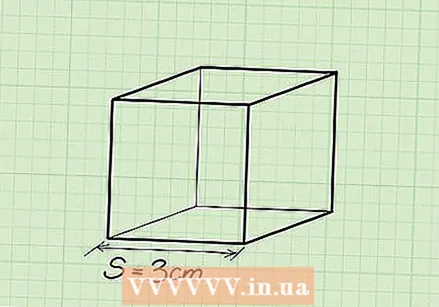2. Determine the length of 1 side of the cube. All sides are the same, so it doesn't matter which one you choose.
   • Ex: Length = 3 cm.
3. The power of three. Multiply the number twice by itself for the cubic number. An example is "a x a x a". Since all side lengths are equal, multiply two sides for the area of ​​the base, and a third side represents the height. You can think of this as a multiplication of the length, width, and height, which are all the same.
   • Ex: 3 cm = 3 cm. * 3 cm. * 3 cm. = 27 cm.
4. Give your answer in cubic units.. The final answer is 27 cm.

Method 3 of 5: Calculate the volume of a rectangular prism

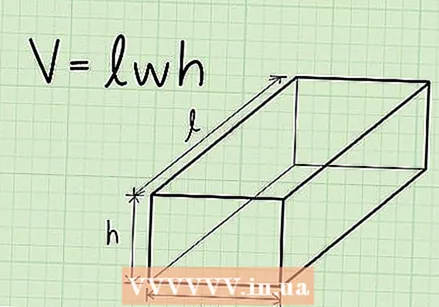1. Write the formula for finding the volume of a rectangular prism. The formula is V = length * width * height. A rectangular prism is a prism with a rectangular base.
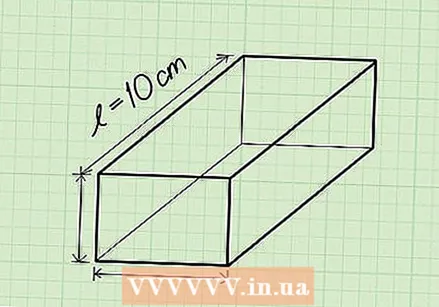2. Determine the length. The length is the longest side of the flat surface of the rectangle, above or at the bottom of the rectangular prism.
   • Ex: Length = 10 cm.
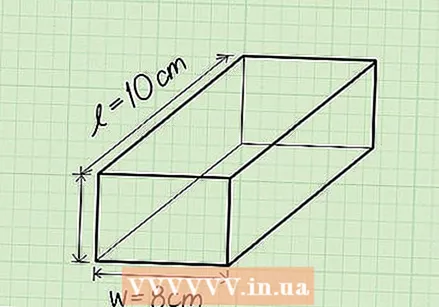3. Determine the width. The width of the rectangular prism is the shorter side of the flat surface of a rectangle, at the top or bottom of the shape.
   • Ex: Width = 8 cm.
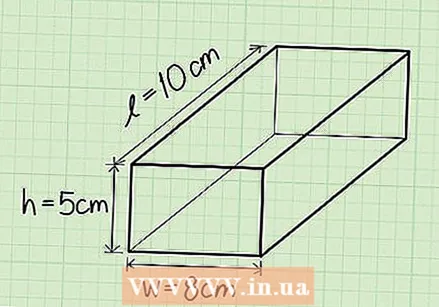4. Determine the height. The height is that part of the rectangular prism that is upright. You can think of the height of the rectangular prism as that part that extends from a rectangle and turns it into a three-dimensional figure.
   • Ex: Height = 5 cm.
5. Multiply the length, width, and height. Multiply these in any order for the product. Use this method to find the area of ​​the rectangular base (10 x 8) and then the volume by multiplying this by the height, 5. But, to find the volume of this prism, you can find the lengths of the multiply each order.
   • Ex: 10 cm. * 8 cm. * 5 cm = 400 cm.
6. Give your answer in cubic units. The final answer is 400 cm.

Method 4 of 5: Calculate the volume of a trapezoidal prism

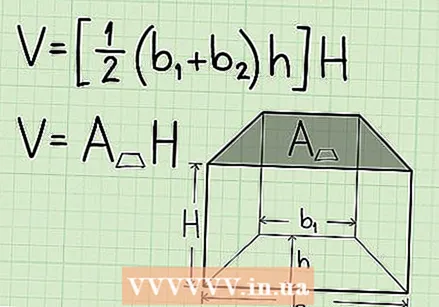1. Write the formula for calculating the volume of a trapezoid. The formula is: V = [1/2 x (base₁ + base₂) x height] x height of the prism. Use the first part for the area of ​​the base of the prism before continuing.
2. Determine the area of ​​the base. To do this, enter the area of ​​the top and bottom in the formula, along with the height.
   • Suppose the base 1 = 8 cm, base 2 = 6 cm, and height = 10 cm.
   • Ex: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm.
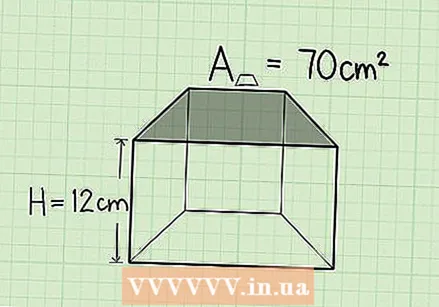3. Determine the height of the prism. Suppose the height of the prism is 12 cm.
4. Multiply the area of ​​the base times the height. To calculate the volume of the trapezoid, multiply the area of ​​the base by the height.
   • 80 cm x 12 cm = 960 cm.
5. Give your answer in cubic units. The final answer is 960 cm

Method 5 of 5: Calculate the volume of a regular pentagonal prism

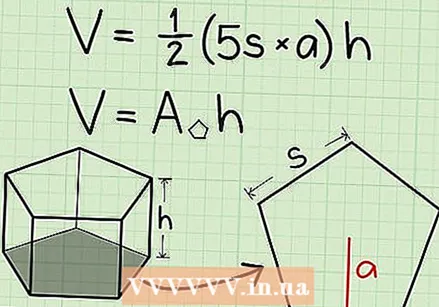1. Write down the formula for finding the volume of a regular pentagonal prism. The formula is V = [1/2 x 5 x side x apothem] x height of the prism. You can use the first part of the formula to find the area of ​​the pentagonal base. Think of this as determining the area of ​​the 5 triangles that make up a regular polygon. The side is the width of 1 triangle, and the apothem is the height of one of the triangles. Now you multiply by 1/2 because that is part of finding the area of ​​a triangle and then you multiply this by 5, because there are 5 triangles in a pentagon.
   • For more information about determining the apothem, you can look here.
2. Find the area of ​​the pentagonal base. Suppose the length of one side is 6 cm and the length of the apothem is 7 cm. Enter the numbers in the formula:
   • A = 1/2 x 5 x side x apothem
   • A = 1/2 x 5 x 6 cm x 7 cm = 105 cm
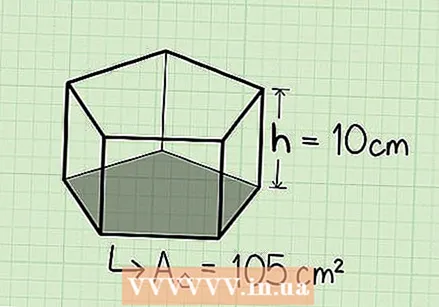3. Determine the height. Suppose the height of the mold is 10 cm.
4. Multiply the area of ​​the pentagonal base times the height. Multiply the area of ​​the pentagonal base, 105 cm, times the height, 10 cm, to find the volume of the regular pentagonal prism.
   • 105 cm x 10 cm = 1050 cm
5. Give your answer in cubic units. The final answer is 1050 cm.

Tips

• Try not to confuse "base" with "base plane". A base plane refers to the two-dimensional shape that is the base of the prism (usually the top and bottom). But that base plane can have its own base --- one of the sides of the shape of the face, used to find the area of ​​that shape.