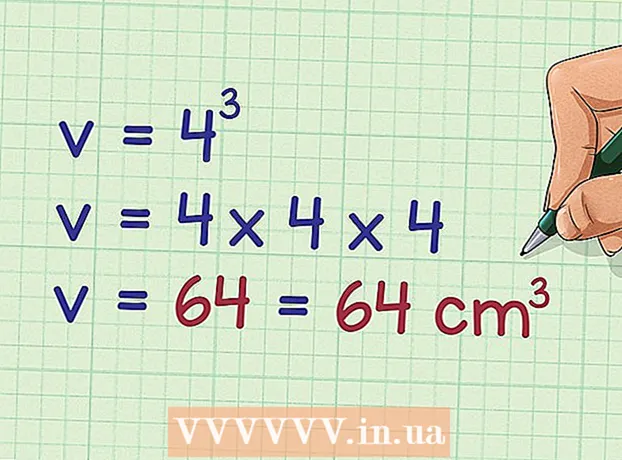Author:
Roger Morrison
Date Of Creation:
27 September 2021
Update Date:
21 June 2024

Content
A prism is a three-dimensional figure with two parallel ground planes, which are congruent. The shape of the base determines what kind of prism it is, such as a rectangular or triangular prism. Since it is a 3D shape, it is not uncommon to want to calculate the volume of a prism; however, you do need the height of the prism for this. Finding the height is possible when you have gotten enough information: either the volume, area and perimeter of the base. The formulas described in the methods below are suitable for prisms with bases of any shape, provided you know the formula for finding the area of that shape.
To step
Method 1 of 4: Determine the height of a rectangular prism with a known volume
 Use the formula for the volume of a prism. The volume of a prism can be found using the formula
Use the formula for the volume of a prism. The volume of a prism can be found using the formula  Apply the volume to the formula. If you don't know the volume, you can't use this method.
Apply the volume to the formula. If you don't know the volume, you can't use this method. - For example, if the volume of the prism is 64
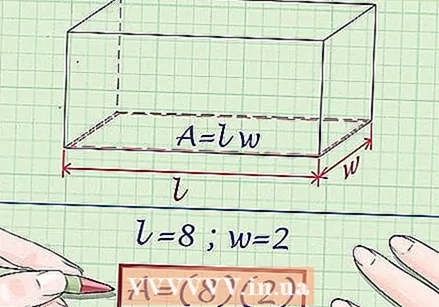 Determine the area of the base. To determine the area, you need to know the length and width of the base (or of a side, if the base is a square). Use the formula
Determine the area of the base. To determine the area, you need to know the length and width of the base (or of a side, if the base is a square). Use the formula  Substitute the area of the ground plane in the volume of the prism formula. Make sure to substitute for the variable
Substitute the area of the ground plane in the volume of the prism formula. Make sure to substitute for the variable  Solve the equation for
Solve the equation for  Write down the formula for the volume of a prism. The volume of any prism can be found using the formula
Write down the formula for the volume of a prism. The volume of any prism can be found using the formula  Apply the volume to the formula. If you don't know the volume, you can't use this method.
Apply the volume to the formula. If you don't know the volume, you can't use this method. - For example, if you know that the volume of the prism is 840 cubic meters (
 Determine the area of the base. To find the area, you need to know the length of the base of the triangle and the height of the triangle. Use the formula
Determine the area of the base. To find the area, you need to know the length of the base of the triangle and the height of the triangle. Use the formula 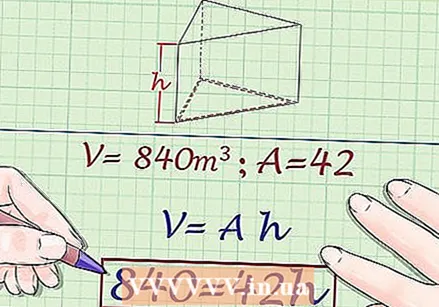 Substitute the area of the ground plane in the volume of the prism formula. Make sure to substitute for the variable
Substitute the area of the ground plane in the volume of the prism formula. Make sure to substitute for the variable  Solve the equation for
Solve the equation for  Write down the formula for the area of a prism. The formula for the area of a prism is
Write down the formula for the area of a prism. The formula for the area of a prism is  Substitute the area of the prism in the formula. If the area is unknown, this method will not work.
Substitute the area of the prism in the formula. If the area is unknown, this method will not work. - For example, if the area is 1460 cm, your formula would look like this:
 Determine the area of the base. To determine the area, you need to know the length and width of the base (or one side, if the base is a square). Use the formula
Determine the area of the base. To determine the area, you need to know the length and width of the base (or one side, if the base is a square). Use the formula  Substitute the area of the base in the formula for the area of a prism, and simplify. Make sure to fill in for the letter
Substitute the area of the base in the formula for the area of a prism, and simplify. Make sure to fill in for the letter  Determine the perimeter of the base. To find the perimeter of a rectangle, add the lengths of all four sides, or multiply the length of one side by 4 if it is a square.
Determine the perimeter of the base. To find the perimeter of a rectangle, add the lengths of all four sides, or multiply the length of one side by 4 if it is a square. - Remember that the opposite sides of a rectangle are the same length.
- For example, if the base is a rectangle with a length of 8 cm and a width of 2 cm, you determine the perimeter as follows:
 Substitute the perimeter of the base in the formula for the area of a prism. Make sure to substitute for the letter
Substitute the perimeter of the base in the formula for the area of a prism. Make sure to substitute for the letter  Solve the equation for
Solve the equation for 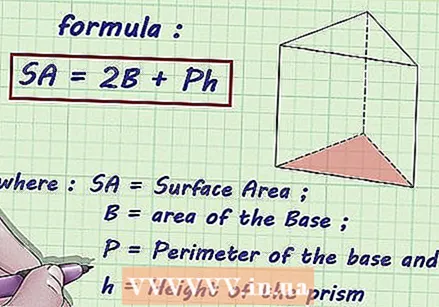 Write down the formula for the area of a prism. The formula for the area of a prism is
Write down the formula for the area of a prism. The formula for the area of a prism is  Substitute the area of the prism in the formula. If the area is unknown, this method will not work.
Substitute the area of the prism in the formula. If the area is unknown, this method will not work. - For example, if the area is 1460 cm, your formula would look like this:
 Determine the area of the base. To determine the area, the length of the base of the triangle and the height of the triangle must be known. Use the formula
Determine the area of the base. To determine the area, the length of the base of the triangle and the height of the triangle must be known. Use the formula  Substitute the area of the base in the formula for the area of a prism and simplify. Substitute for
Substitute the area of the base in the formula for the area of a prism and simplify. Substitute for  Determine the perimeter of the base. To find the perimeter of a triangle, add the length of all three sides together.
Determine the perimeter of the base. To find the perimeter of a triangle, add the length of all three sides together. - For example, if the base is a triangle with the lengths 8, 4 and 9 cm, you calculate the perimeter as follows:
 Substitute the perimeter of the base in the formula for the area of a prism. Make sure you substitute for
Substitute the perimeter of the base in the formula for the area of a prism. Make sure you substitute for  Solve the equation for
Solve the equation for . Now you know the height of your prism.
- For example, in the equation
, you must first subtract 32 from each side, then divide each side by 21. Thus:
- So, the height of your prism is 68 cm.
- For example, in the equation
- For example, if the base is a triangle with the lengths 8, 4 and 9 cm, you calculate the perimeter as follows:
- For example, if the area is 1460 cm, your formula would look like this:
- For example, if the area is 1460 cm, your formula would look like this:
- For example, if you know that the volume of the prism is 840 cubic meters (
- For example, if the volume of the prism is 64
Necessities
- Pen / pencil and paper or calculator (optional)