Content

• To step
• Method 1 of 2: Use a table

The Fibonacci sequence is a sequence of numbers generated by adding the previous two numbers in the sequence. The numbers in the series are frequently reflected in nature and in art, such as spirals and the golden ratio. The easiest way to calculate the series is to create a table; however, this is not practical if, for example, you are looking for the 100th term in the sequence, in which case you are using Binet's formula.

To step

Method 1 of 2: Use a table

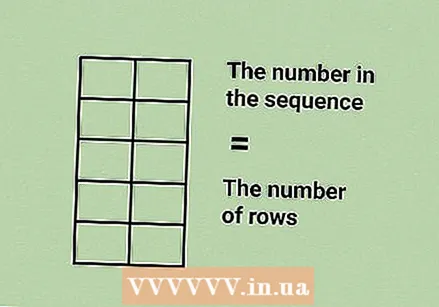1. Create a table with two columns. The number of rows depends on the number of numbers in the Fibonacci sequence you want to calculate.
   • For example, if you want to find the fifth number in the sequence, your table will get five rows.
   • With this table method, it is not possible to find a random number further down the sequence without calculating all the numbers for it first. For example, if you want to find the 100th number in the sequence, you will have to find the first 99 numbers first. Therefore, the table method only works for numbers at the beginning of the sequence.
2. Enter the sequence of numbers in the left column. This means entering a series of consecutive ordinal numbers starting with "1st."
   • The term refers to the position of the number in the Fibonacci sequence.
   • For example, if you want to calculate the fifth number in the sequence, write 1st, 2nd, 3rd, 4th, 5th down the left column. This will clarify the first five terms of the sequence.
3. Put 1 in the first row of the right column. This is the starting point of the Fibonacci sequence. In other words, the first term in the series is 1.
   • The correct Fibonacci sequence always starts with 1. If you want to start with another number, you will not find the correct pattern for the Fibonacci sequence.
4. Count the first term (1) and 0. Together. This will give you the second number in the sequence.
   • Remember, to find a given number of the Fibonacci sequence, you just need to add the two previous numbers.
   • To create the sequence, 0 comes before the 1 (the first term), so: 1 + 0 = 1.
5. Add the first term (1) and the second term (1) together. This will give you the third number in the sequence.
   • 1 + 1 = 2. The third term is 2.
6. Add the second term (1) and the third term (2) to get the fourth number in the sequence.
   • 1 + 2 = 3. The fourth term is 3.
7. Add the third term (2) and the fourth term (3) together. Now you know the fifth number in the sequence.
   • 2 + 3 = 5. The fifth term is 5.
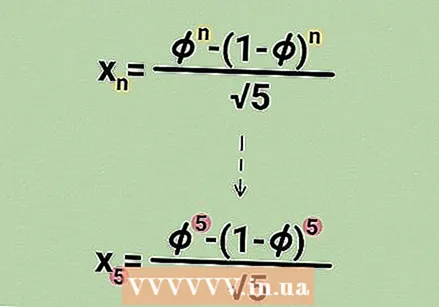8. Add the previous two numbers to find any given number in the Fibonacci sequence. If you use this method, you use the formula ${ displaystyle F_ {n} = F_ {n-1} + F_ {n-2}}$Write down the formula:${ displaystyle x_ {n}}$Pass the number for n{ displaystyle n}Substitute the golden ratio in the formula. Use 1.618034 as an approximation of the golden ratio.
   • For example, if you search for the fifth number in the sequence, the entered formula will look like this: ${ displaystyle x_ {5}}$Complete the calculations in parentheses. Consider the order of arithmetic operations by first calculating the part in brackets: ${ displaystyle 1-1.618034 = -0.618034}$Calculate the exponents. Multiply the two numbers in parentheses in the numerator by the correct exponent.
     • In the example, ${ displaystyle 1.618034 ^ {5} = 11.090170}$Complete the calculation. Before you continue to divide, you must first subtract the two numbers in the numerator.
       • In the example, ${ displaystyle 11.090170 - (- 0.090169) = 11.180339}$Divide by the square root of five. The square root of five is rounded to 2.236067.
         • In the example problem, ${ displaystyle { frac {11.180339} {2.236067}} = 5.000002}$Round to the nearest whole number. Your answer is a decimal number, but it is very close to an integer. This integer represents the number in the Fibonacci sequence.
           • If you have used the full golden ratio and have not rounded anything, you will get a whole number. However, it is more practical to round, which will result in a decimal.
           • In the example, your answer, calculated with a calculator, will be approximately 5.000002. Rounded to the nearest whole number, your answer becomes five, which is also the fifth number in the Fibonacci sequence.