Content

• To step

Subtracting fractions with the same denominators is easy, but unlike denominators may require a number of different steps to make the denominators equal so that they can be easily subtracted from each other. These steps take a little more time, but if you get good at them, you will be able to subtract fractions in an instant. If you want to know how to do this, follow these steps.

To step

1. Find the denominators of the fractions. If you want to subtract fractions, the first thing to do is make sure they have the same denominator. The numerator is the number above the fraction line and the denominator is the number below the fraction line. In the example, 3/4 - 1/3, the two denominators of the fraction are 4 and 3. Circle them.
   • If the denominators of the fractions are the same, you can just subtract the numerators leaving the denominator the same. As an example, 4/5 - 3/5 = 1/5. If the fraction is simplified like this, you are done right away.
2. Find the least common multiple (LC) of the denominators. The LCM of two numbers is the smallest number that is divisible by both denominators. You should find the LCV of 4 and 3 here. This will give you the smallest common denominator of the fraction. Here's a great method you can use when it comes to small numbers:
   • List the first pair of multiples of 4: 4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, 4 x 4 = 16
   • List the first pair of multiples of 3: 3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12
   • Stop once you find a common multiple. You can see that 12 is a multiple of both 4 and 3. Since this is the smallest number, you can stop here.
     • Note that you can do this for all types of numbers, including integers and mixed fractions. For the integers, imagine that the denominator is 1. (So, 2 = 2/1.) For mixed fractions, rewrite it as an improper fraction. (So, 2 1/2 = 5/2.)
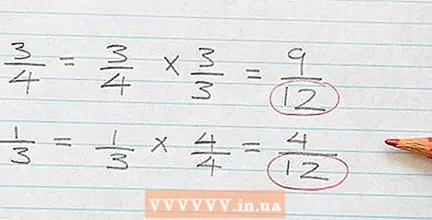3. Make sure that the numerators of the fractions change with it. Now that you know that the lcm of 4 and 3 is equal to 12, take this number as the new denominator of the fractions. But to make the fractions equivalent, you have to multiply the numerators by a number that ensures that the numerator and denominator are in the correct ratio again. Here's how:
   • For the fraction 3/4, you know that the denominator has to be 12, so you need to find the number that multiplied by 4 to get the number 12. 4 x 3 = 12, so multiply 3/4 by 3/3 so that the numerator and denominator remain in the correct ratio. So 3/4 can be rewritten as 9/12.
   • For the fraction 1/3, you know that the denominator has to be 12, so you need to find the number that multiplied by 4 to get the number 12. 4 x 3 = 12, so multiply 1/3 by 4/4 so that the numerator and denominator remain in the correct ratio. 1/4 can therefore be rewritten as 4/12.
4. Write the new numerators above the smallest common denominator. Now that you know that the least common multiple of 4 and 3 is equal to 12, it is possible to say that the least common denominator of fractions 1/3 and 3/4 is equal to 12. Now that you also know the new numerators, you can just write it above the denominator as one fraction, with subtracted numerators. Just make sure to write the counters in the correct order or you will get a wrong answer. Here's how to unsubscribe:
   • 3/4 - 1/3 = 9/12 - 4/12
   • 9/12 - 4/12 = (9-4)/12
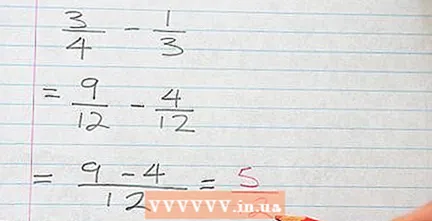5. Subtract the counters. Once you have placed the new numerators above the common denominator, you can subtract them from each other.
   • 9-4 = 5, so 9/12 - 4/12 = 5/12
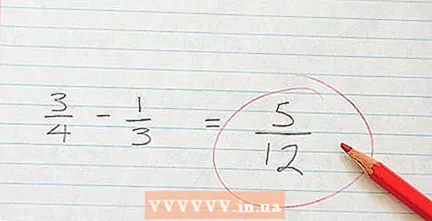6. Simplify your answer. Have you found the answer, check it and simplify if possible. If the numerator and denominator can be divided by the same number, do so. Remember that fractions indicate a ratio, so whatever you do with the denominator, do the same with the numerator. Do not divide one number without dividing the other by the same number. 5/12 will remain as it is because it cannot be simplified further.
   • For example, the fraction 6/8 can be simplified because both 6 and 8 are divisible by 2. The simplified answer then becomes: 6/2 = 3, 8/2 = 4, so 6/8 = 3/4.