Content

• Steps
• Method 1 of 4: Radius
• Method 2 of 4: By Diameter
• Method 3 of 4: Circumference
• Method 4 of 4: By area of ​​a sector of a circle

Some students do not understand how to find the area of ​​a circle from the original data. First you need to remember the formula by which the area of ​​the circle is calculated: ${ displaystyle S = pi r ^ {2}}$... The formula is simple: to find the area of ​​a circle, you only need to know its radius. But you need to be able to transform other initial values ​​in order to use this formula.

Steps

Method 1 of 4: Radius

1. 1 Find the radius of the circle. A radius is a line segment that connects the center of the circle to any point on the outer circumference of the circle. The radius can be measured in any direction: it will be the same. The radius is also half the diameter of the circle. The diameter is the line segment that goes through the center of the circle and connects two points on the outer circumference of the circle.
   • As a rule, the value of the radius is given in the conditions of the problem. It is quite difficult to find the exact center of a circle, unless it is marked on a circle that is drawn on paper.
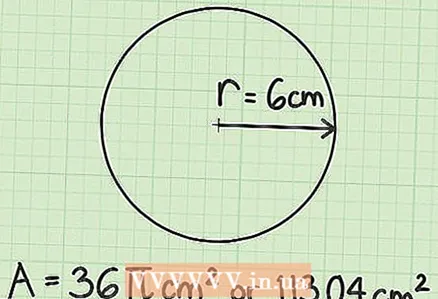
   • For example, the radius of a circle is 6 cm.
2. 2 Square the radius. Formula for calculating the area of ​​a circle: ${ displaystyle S = pi r ^ {2}}$, where ${ displaystyle r}$ - the radius, which is raised to the second power (squared).
   • You don't need to square the whole formula.
   • In our example: ${ displaystyle r = 6}$, so ${ displaystyle r ^ {2} = 36}$.
3. 3 Multiply the result by pi. This number is denoted by a Greek letter ${ displaystyle pi}$ and is a mathematical constant that characterizes the relationship between the radius and area of ​​a circle. Pi is approximately 3.14. The exact meaning of pi includes an infinite number of digits. Sometimes the answer (area of ​​the circle) is written with a constant ${ displaystyle pi}$.
   • In our example (r = 6 cm), the area is calculated as follows:
     • ${ displaystyle S = pi r ^ {2}}$
     • ${ displaystyle S = pi 6 ^ {2}}$
     • ${ displaystyle S = 36 pi}$ or ${ displaystyle S = 36 (3.14) = 113.04}$
4. 4 Write down your answer. Remember that area is measured in square units. If the radius is given in centimeters, the area is measured in square centimeters. If the radius is given in millimeters, the area is measured in square millimeters. Check with your teacher if you need to provide an answer with a constant ${ displaystyle pi}$ or numerically using the approximate value of pi. If the requirement is not clear, write down both answers.
   • In our example (r = 6 cm) S = 36${ displaystyle pi}$ cm or S = 113.04 cm.

Method 2 of 4: By Diameter

1. 1 Measure or write down the diameter. In some problems, the radius is not given. The diameter is indicated instead of the radius. If the diameter is drawn on paper, measure it with a ruler. Most likely, a numeric value for the diameter will be specified.
   • For example, the diameter of a circle is 20 mm.
2. 2 Divide the diameter in half. Remember that the diameter is twice the radius. So divide any diameter value by 2 to find the radius.
   • Thus, if the diameter of the circle is 20 mm, then the radius of the circle is 20/2 = 10 mm.
3. 3 Use the standard formula to calculate the area of ​​a circle. Having found the radius, use the formula ${ displaystyle S = pi r ^ {2}}$to calculate the area of ​​the circle. Plug in the radius value and calculate as follows:
   • ${ displaystyle S = pi r ^ {2}}$
   • ${ displaystyle S = pi 10 ^ {2}}$
   • ${ displaystyle S = 100 pi}$
4. 4 Write down your answer. Remember that area is measured in square units. In our example, the diameter is given in millimeters, so the radius is also measured in millimeters, and the area in square millimeters. In our example, S = ${ displaystyle 100 pi}$ mm.
   • Also, the answer can be presented in numerical form, using instead of ${ displaystyle pi}$ an approximate value of 3.14. In this case, S = (100) (3.14) = 314 mm.

Method 3 of 4: Circumference

1. 1 Write down the converted formula. If you know the circumference of a circle, you can use the transformed formula to calculate its area. Such a formula includes the circumference, not the radius, and is written like this: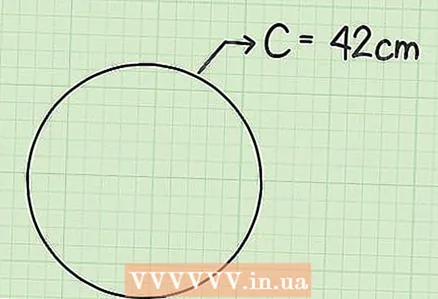
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$
2. 2 Measure or write down the circumference. In some situations, the diameter or radius cannot be accurately measured. If the diameter is not drawn or the center is not marked, it is very difficult to find the exact center of the circle. The circumference of some objects (for example, frying pans) is quite easy to measure with a tape measure, that is, you can find a more accurate value for the circumference than the diameter.
   • For example, the circumference of a circle (or round object) is 42 cm.
3. 3 Use the ratio between circumference and radius to rewrite the formula. The circumference is equal to Pi times the diameter. It can be written like this: ${ displaystyle C = pi d}$... Recall that the diameter is equal to twice the radius, that is ${ displaystyle d = 2r}$... Combine these equalities to write the following formula: ${ displaystyle C = pi 2r}$... Now isolate the variable ${ displaystyle r}$:
   • ${ displaystyle C = pi 2r}$
   • ${ displaystyle { frac {C} {2 pi}} = r}$ (divide both sides by 2${ displaystyle pi}$)
4. 4 Write down a formula for calculating the area of ​​a circle. Write down the converted formula based on the relationship between the circumference and the radius. Plug the last equation into the standard formula for calculating the area of ​​a circle:
   • ${ displaystyle S = pi r ^ {2}}$ (standard formula)
   • ${ displaystyle S = pi ({ frac {C} {2 pi}}) ^ {2}}$ (an expression was substituted for r)
   • ${ displaystyle S = pi ({ frac {C ^ {2}} {4 pi ^ {2}}})}$ (squared fraction)
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$ (reduced ${ displaystyle pi}$ in the numerator and in the denominator)
5. 5 Use the transformed formula to solve the problem. Now in the formula, instead of the radius, there is a circumference, so you can calculate the area of ​​a circle using a known circumference. Plug in the circumference and calculate as follows:
   • In our example ${ displaystyle C = 42}$ cm.
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$
   • ${ displaystyle S = { frac {42 ^ {2}} {4 pi}}}$ (substituted value)
   • ${ displaystyle S = { frac {1764} {4 pi}}}$ (calculated 42)
   • ${ displaystyle S = { frac {441} { pi}}}$ (divided by 4)
6. 6 Write down your answer. If the circumference is given as a number, not the product of a number and ${ displaystyle pi}$, the answer can be written with ${ displaystyle pi}$ in the denominator. Or substitute the approximate value of Pi (3.14) instead of Pi.
   • In our example (C = 42 cm) S = ${ displaystyle { frac {441} { pi}}}$ cm.
   • Or like this: S = ${ displaystyle { frac {441} { pi}} = { frac {441} {3.14}} = 140.4}$ cm.

Method 4 of 4: By area of ​​a sector of a circle

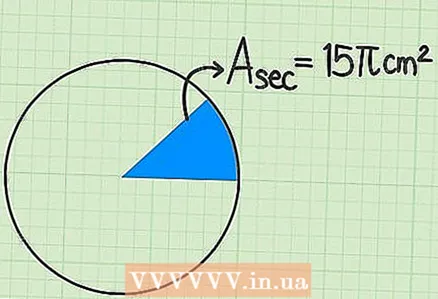1. 1 Write down the known values. In some problems, the area of ​​a sector of a circle is given, by which you need to find the area of ​​the entire circle. Read this problem carefully; its condition may look like this: “The area of ​​the sector of the circle is 15${ displaystyle pi}$ see Find the area of ​​the whole circle. "
2. 2 Remember the sector definition. A sector of a circle is the part of a circle that is bounded by an arc and two radii. The space between such radii and the arc is called a sector.
3. 3 Measure the center angle of the sector. Use a protractor to measure the angle between the two radii. Align the ruler (straight scale) with one of the radii, and the center of the ruler should coincide with the center of the circle. Then find the value of the angle; to do this, look at the point of intersection of the second radius with the goniometric scale.
   • Don't confuse the inside and outside corner between the two radii. The task should indicate which angle to work with. Remember that the sum of the inside and outside angles is 360 degrees.
   • In many problems, the central angle is given, that is, you do not need to measure it. For example, the problem may say: "The central angle of the sector is 45 degrees"; if not, measure the center angle.
4. 4 Use the converted formula to calculate the area of ​​a circle. If you know the area of ​​the sector and its center angle, use the following transformed formula to find the area of ​​a circle:
   • ${ displaystyle S_ {kr} = S_ {sek} { frac {360} {C}}}$
     • ${ displaystyle S_ {kr}}$ - area of ​​a circle
     • ${ displaystyle S_ {sek}}$ - sector area
     • ${ displaystyle C}$ - central corner
5. 5 Plug in the known values ​​and find the area of ​​the circle. In our example, we know that the central angle is 45 degrees, and the area of ​​the sector is 15${ displaystyle pi}$... Plug these values ​​into the formula:
   • ${ displaystyle S_ {kr} = S_ {sek} { frac {360} {C}}}$
   • ${ displaystyle S_ {kr} = 15 pi { frac {360} {45}}}$
   • ${ displaystyle S_ {kr} = 15 pi (8)}$
   • ${ displaystyle S_ {kr} = 120 pi}$
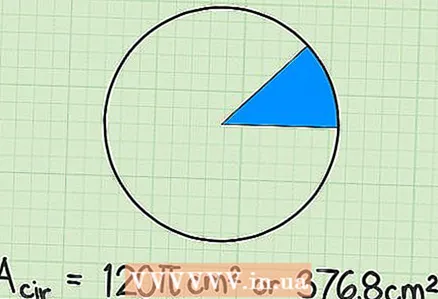6. 6 Write down your answer. In our example, the sector was one-eighth of a full circle. Therefore, the area of ​​a complete circle is 120${ displaystyle pi}$ cm. Since the area of ​​the sector is given with a constant ${ displaystyle pi}$most likely, the answer can also be presented with this constant.
   • To write your answer numerically, multiply 120 x 3.14 = 376.8 cm.