Content

• Steps
• Method 1 of 3: How to solve a cubic equation without a constant term
• Method 2 of 3: How to Find Whole Roots Using Multipliers
• Method 3 of 3: How to Solve an Equation Using the Discriminant

In a cubic equation, the highest exponent is 3, such an equation has 3 roots (solutions) and it has the form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Some cubic equations are not so easy to solve, but if you apply the right method (with good theoretical background), you can find the roots of even the most complex cubic equation - for this use the formula for solving the quadratic equation, find the whole roots, or calculate the discriminant.

Steps

Method 1 of 3: How to solve a cubic equation without a constant term

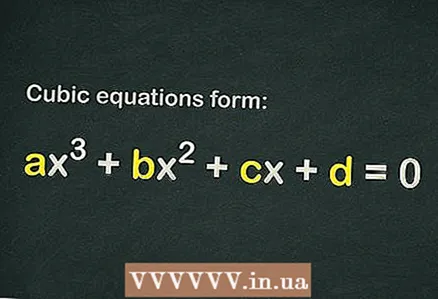1. 1 Find out if there is a free term in the cubic equation d{ displaystyle d}. The cubic equation has the form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... For an equation to be considered cubic, it is sufficient that only the term ${ displaystyle x ^ {3}}$ (that is, there may be no other members at all).
   • If the equation has a free term ${ displaystyle d}$, use a different method.
   • If in the equation ${ displaystyle a = 0}$, it is not cubic.
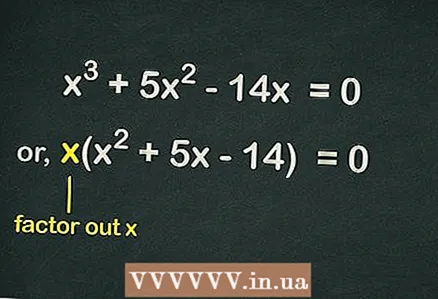2. 2 Take out of the brackets x{ displaystyle x}. Since there is no free term in the equation, each term in the equation includes the variable ${ displaystyle x}$... This means that one ${ displaystyle x}$ can be excluded from parentheses to simplify the equation. Thus, the equation will be written like this: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • For example, given a cubic equation ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Take out ${ displaystyle x}$ brackets and get ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
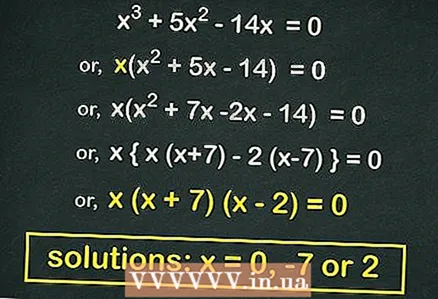3. 3 Factor (the product of two binomials) the quadratic equation (if possible). Many quadratic equations of the form ${ displaystyle ax ^ {2} + bx + c = 0}$ can be factorized. Such an equation will turn out if we take out ${ displaystyle x}$ outside the brackets. In our example:
   • Take out of the brackets ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Factor the quadratic equation: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Equate each bin to ${ displaystyle 0}$... The roots of this equation are ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Solve a quadratic equation using a special formula. Do this if the quadratic equation cannot be factorized. To find two roots of an equation, the values ​​of the coefficients ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ substitute in the formula ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • In our example, substitute the values ​​of the coefficients ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) into the formula:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • First root:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Second root:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Use zero and quadratic roots as solutions to the cubic equation. Quadratic equations have two roots, while cubic ones have three. You have already found two solutions - these are the roots of the quadratic equation. If you put "x" outside the brackets, the third solution would be ${ displaystyle 0}$.
   • If you take "x" out of the brackets, you get ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, that is, two factors: ${ displaystyle x}$ and a quadratic equation in brackets. If any of these factors is ${ displaystyle 0}$, the whole equation is also equal to ${ displaystyle 0}$.
   • Thus, two roots of a quadratic equation are solutions of a cubic equation. The third solution is ${ displaystyle x = 0}$.

Method 2 of 3: How to Find Whole Roots Using Multipliers

1. 1 Make sure there is a free term in the cubic equation d{ displaystyle d}. If in an equation of the form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ there is a free member ${ displaystyle d}$ (which is not equal to zero), it will not work to put "x" outside the brackets. In this case, use the method outlined in this section.
   • For example, given a cubic equation ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... To get zero on the right side of the equation, add ${ displaystyle 6}$ to both sides of the equation.
   • The equation will turn out ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... As ${ displaystyle d = 6}$, the method described in the first section cannot be used.
2. 2 Write down the factors of the coefficient a{ displaystyle a} and a free member d{ displaystyle d}. That is, find the factors of the number at ${ displaystyle x ^ {3}}$ and numbers before the equal sign. Recall that the factors of a number are the numbers that, when multiplied, produce that number.
   • For example, to get the number 6, you need to multiply ${ displaystyle 6 times 1}$ and ${ displaystyle 2 times 3}$... So the numbers 1, 2, 3, 6 are factors of the number 6.
   • In our equation ${ displaystyle a = 2}$ and ${ displaystyle d = 6}$... Multipliers 2 are 1 and 2... Multipliers 6 are the numbers 1, 2, 3 and 6.
3. 3 Divide each factor a{ displaystyle a} for each factor d{ displaystyle d}. As a result, you get a lot of fractions and several integers; the roots of the cubic equation will be one of the whole numbers or the negative value of one of the whole numbers.
   • In our example, divide the factors ${ displaystyle a}$ (1 and 2) by factors ${ displaystyle d}$ (1, 2, 3 and 6). You'll get: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ and ${ displaystyle { frac {2} {3}}}$... Now add negative values ​​of the obtained fractions and numbers to this list: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ and ${ displaystyle - { frac {2} {3}}}$... The whole roots of the cubic equation are some numbers from this list.
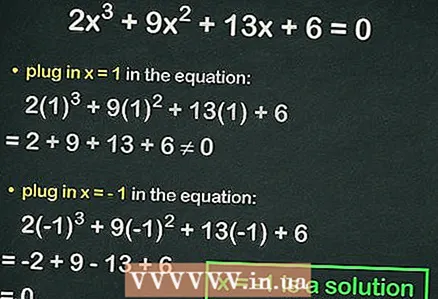4. 4 Plug in integers into the cubic equation. If the equality is true, the substituted number is the root of the equation. For example, substitute in the equation ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, that is, equality is not observed. In this case, plug in the next number.
   • Substitute ${ displaystyle -1}$: ${ displaystyle (-2) +9 + (- 13) +6}$ = 0. Thus, ${ displaystyle -1}$ is the whole root of the equation.
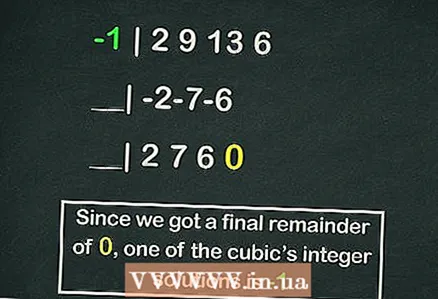5. 5 Use the method of dividing polynomials by Horner's schemeto find the roots of the equation faster. Do this if you don't want to manually substitute numbers into the equation. In Horner's scheme, integers are divided by the values ​​of the coefficients of the equation ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ and ${ displaystyle d}$... If the numbers are evenly divisible (that is, the remainder is ${ displaystyle 0}$), the integer is the root of the equation.
   • Horner's scheme deserves a separate article, but the following is an example of calculating one of the roots of our cubic equation using this scheme:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • So the remainder is ${ displaystyle 0}$, but ${ displaystyle -1}$ is one of the roots of the equation.

Method 3 of 3: How to Solve an Equation Using the Discriminant

1. 1 Write down the values ​​of the coefficients of the equation a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} and d{ displaystyle d}. We recommend that you write down the values ​​of the indicated coefficients in advance so as not to get confused in the future.
   • For example, given the equation ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Write down ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ and ${ displaystyle d = -1}$... Recall that if before ${ displaystyle x}$ there is no number, the corresponding coefficient still exists and is equal to ${ displaystyle 1}$.
2. 2 Calculate the zero discriminant using a special formula. To solve a cubic equation using the discriminant, you need to perform a number of difficult calculations, but if you perform all the steps correctly, this method will become indispensable for solving the most complex cubic equations. First compute ${ displaystyle Delta _ {0}}$ (zero discriminant) is the first value we need; to do this, substitute the corresponding values ​​in the formula ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • The discriminant is a number that characterizes the roots of a polynomial (for example, the discriminant of a quadratic equation is calculated by the formula ${ displaystyle b ^ {2} -4ac}$).
   • In our equation:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Calculate the first discriminant using the formula Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. First discriminant ${ displaystyle Delta _ {1}}$ - this is the second important value; to calculate it, plug the corresponding values ​​into the specified formula.
   • In our equation:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Calculate:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... That is, find the discriminant of the cubic equation through the obtained values ${ displaystyle Delta _ {0}}$ and ${ displaystyle Delta _ {1}}$... If the discriminant of a cubic equation is positive, the equation has three roots; if the discriminant is zero, the equation has one or two roots; if the discriminant is negative, the equation has one root.
   • A cubic equation always has at least one root, since the graph of this equation intersects the X-axis at least at one point.
   • In our equation ${ displaystyle Delta _ {0}}$ and ${ displaystyle Delta _ {1}}$ are equal ${ displaystyle 0}$, so you can easily calculate ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Thus, our equation has one or two roots.

5. 5 Calculate:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } right) div 2}}}$. ${ displaystyle C}$ - this is the last important quantity to be found; it will help you calculate the roots of the equation. Substitute the values ​​into the specified formula ${ displaystyle Delta _ {1}}$ and ${ displaystyle Delta _ {0}}$.
   • In our equation:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Find three roots of the equation. Do it with the formula ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, where ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, but n is equal to 1, 2 or 3... Substitute the appropriate values ​​into this formula - as a result, you get three roots of the equation.
   • Calculate the value using the formula at n = 1, 2 or 3and then check the answer. If you get 0 when you check your answer, this value is the root of the equation.
   • In our example, substitute 1 in ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ and get 0, i.e 1 is one of the roots of the equation.